Last edited 2apr14, 23apr14
\begin{document}
Jump to Part II
\maketitle
Syllabus "Post-Euclidian Geometry"
MA402 Spring 2014
Instructions
This file is frequently updated. Check the date and reload your browser
pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due"
in the syllabus.
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by
section and number, e.g. "C2" for the second lesson in
Cartesian Geometry.
This syllabus overrides all other instructions, in case of an inadvertent conflict.
Part I of the Course
Geometry and the Axiomatic Method [Hvidsten Chapter 1]
\begin{itemize}
\item W1 [1.1, 1.2] Lesson A1:
Greek Geometry from Thales to Pappus with associated Filecard due before class F1.
\item F1 Lesson A2:
Exterior Angle Lab I Introduction to Geometry Explorer (GEX2.0) with filecard due before class M2. (Lab report is due in 3 weeks.)
\item Homework for M2: Read
Introduction to Post-Modern Geometry .
\item Homework for M2: Browse
Advice for Completing this Course. Mark this link to consult throughout the course.
\item M2 Lessons on
Mathematical Typesetting as discussed in Advice. General Administrivia and Introduction to the Course.
\item W2 Lesson A3:
Axiomatic Systems in Geometry
\item W2 [1.4] Lesson A4:
Toy Axiom System better known as Finite Geometries. Filecard is due before class.
\item F2 Lesson A5:
Exterior Angle Lab II . Introduction to models of non-Euclidean geometry.
\item M3 [1.5] Lesson A6:
Models of Axiomatic Systems .
\item W3 Submit
HomeworkM3 on axiomatic systems on Moodle. Do Hvidsten 1.5.4, 1.5.5., 1.5.6, 1.5.7 as directed, using models.
\item F3 Review and
Sample Quiz
\item M4
QuizA. This quiz tests lessons A1-A6 and elementary skills GEX2.0. Be sure to bring your Journal to class with you.
\end{itemize}
Euclid's Geometry [Hvidsten Chapter 2]
\begin{itemize}
\item W4 [2.1] Lesson E1 on
Absolute Geometry with filecard.
\item F4 [2.2] Lesson E2 on
Euclid's Parallel Postulate with filecard.
\item M5 [2.3] Lesson E3 on
John Playfair's Axiom and its equivalents. Filecard TBA.
\item W5 Submit HomeworkM5 on Euclid's Parallel Postulate as posed in Lesson E2.
\item F5 Lesson E4 on the
Pythagorean Theorem as Euclid proved it. Has filecard.
\item W5 Review
\item M6
QuizE . This is an in-class quiz testing lessons
E1--E3 on Euclid's geometry.
\end{itemize}
Cartesian Geometry a.k.a. Analytic Geometry.
\begin{itemize}
\item W6 [2.5] Lesson C1 on
Similarity , ladder lemma, AAA, and simSAS.
\item F6 Lesson C2 on
Cartesian Geometry as Model for Birkhoff's Axioms
\item F6 Lesson C3 on
Circular Numbers needed for Birkhoff's Protractor Axiom.
\item F6 Submit
HomeworkF6 on Birkhoff's Axioms.
\item M7 Advice on preparing for the
Midterm
\item W7
Midterm
\end{itemize}
Part II of the Course
The second 8 weeks of this course deals with the modern approach to
geometry in terms of Transformation Groups, in particular the group of
Moebius Transformation and its subgroups. The Syllabus will be filled
in as lessons become ready and relevant. Please consult the Syllabus
daily and be sure to update your browser.
\begin{itemize}
\item F7
Overview of Lessons on Models, Part I.
\item M8 [3.5]
The Complex Plane and
Euler's Theorem. Filecard Z1 questions due.
\item W8 Discussion of Midterm.
\item F8 Lesson on
Moebius Transformations .
Filecard Z2 is due.
\item M9 Q/A on
Problems 3.5.1 -- 3.5.5 in Hvidsten.
\item W9 Lesson on
Cross Ratios with filecard Z3
\item F9 No Class.
\item M10
Discussion of the Exercises 8.2.1-15
\item W10 Submit Exercises 8.2.8, 8.2.2, and 8.2.3, and the two extensions.
<\item W10
Supplement for reference,
as discussed in this session.
\item W10 Lesson on
Hyperbolic Group with filecard H1.
\item F10
Sample Quiz on Moebius Transformations.
\item M11 Lesson on
Hyperbolic Distance with filecard H2.
\item W11
QuizZ . This is an in-class quiz testing lessons Z1, Z2, Z3, H1, on the geometry of the Euclidean plane using complex numbers and M\"obius Transformations.
\item F11 Lesson on
Hyperbolic Translation with filecard H3.
\end{itemize}
Area Hyperbolic Triangle is its Angular Defect
\begin{itemize}
\item M12
Gauss' theorem on areas
\item W12 Gauss' theorem cont'd
\item F12 Review of Lessons H1,H2,H3 (sample quiz).
\item M13
QuizH is postponed
\item M13 Gauss' theorem concluded.
\end{itemize}
Isomorphism between Models of Hyperbolic Geometry
\begin{itemize}
\item W13
Three Equivalent Models
\item W13
HyperSpace (for macs)
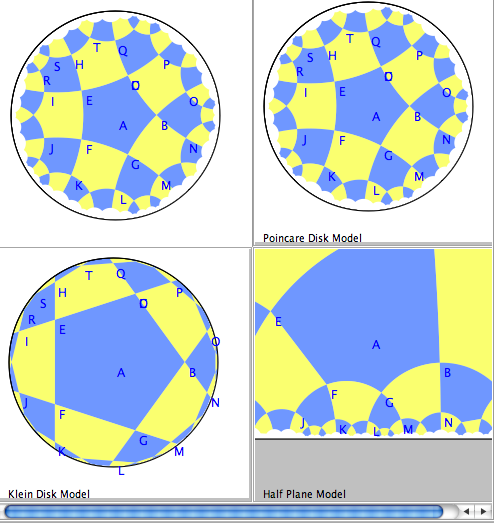
\item W13 Poincare-Klein sketch
\item F13 Takehome Quiz H is due M14. It is posted on the Moodle. If you did not get a Moodle notification, or you cannot access the Moodle, you must email me immediately.
\item F13 Equivalence theorem for the various models.
\item M14 Review of the second half of the course.
\item W14 Review of Axiomatic Methods, Absolute Geometry, and Playfair.
\item F14 Review of Euclidean and Cartesian Geometry. Essay topics on final.
\item M15 Return tests and back homework.
\item W15 Private consultations, see signup sheet.
\item F15 Final Exam, 1:30 - 4:30 pm, 24 IH.
\item R16 Conflict Final. 7:00-10:00 pm, 24IH. Consult with me to establish a conflict.
\end{itemize}
\end{document}  pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due"
in the syllabus.
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by
section and number, e.g. "C2" for the second lesson in
Cartesian Geometry.
This syllabus overrides all other instructions, in case of an inadvertent conflict.
pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due"
in the syllabus.
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by
section and number, e.g. "C2" for the second lesson in
Cartesian Geometry.
This syllabus overrides all other instructions, in case of an inadvertent conflict.
 pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due"
in the syllabus.
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by
section and number, e.g. "C2" for the second lesson in
Cartesian Geometry.
This syllabus overrides all other instructions, in case of an inadvertent conflict.
pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due"
in the syllabus.
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by
section and number, e.g. "C2" for the second lesson in
Cartesian Geometry.
This syllabus overrides all other instructions, in case of an inadvertent conflict.