Miscellaneous Advice for the Midterm 
\textit{$\C$  2010, Prof. George K. Francis, Mathematics Department,
University of Illinois} 

\begin{document}
\maketitle



\section{Introduction}
Here are comments on the Problem 1-6 for this week, in reverse order. 

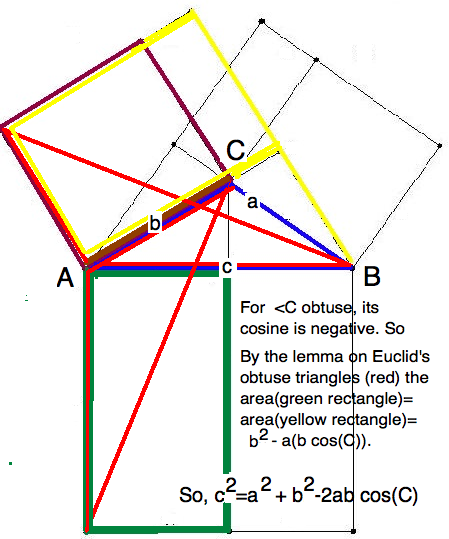
\subsection{Law of Cosines, obtuse case.}
The essential feature is to realize that the figure for the Lemma looks different here. In the above
iPaint sketch, we begin with $\angle BAC$, which is obtuse
at $C$. Building the squares on just these two legs, drop the altitude from 
$C$ to cut the big square
into two rectangles.We still have Euclid's argument about the
congruence of the two yellow, obtuse triangles. And the one with side $AC$ is still equal in area
to the left rectangle on the base. But the argument for the second triangle, 
(triangles with the same base and the same height are of equal area) requires you add the red lines 
to the figure. The red altitude from $B$ is parallel to the side of the little square. So the 
left rectangle inside the big square exceeds the area of the little square by the rectangle formed
from the 3 red sides.

Note that the cosine of an obtuse angle is negative, so subtracting is actually
adds something positive. So we augment the squares on the sides by two rectangles, each equal to $- ab \cos(C)$ for different reasons.

\subsection{Geometric proof of the Law of Cosines, acute case.}
This is already in the notes earlier on.

\subsection{An application of the Law of Cosines}
An interesting application is the verification of the simSAS axiom of 
Birkhoff. Given a triangle with sides $a,b,c$ and angles $\alpha, \beta, 
\gamma $, what happens to the triangle if, while keeping the angle $\gamma$
unchanged, we stretch/shrink \textbf{both} sides by the same amount $t>0$. 
Clearly, the new sides flanking the angle have lengths $ ta, tb$. So, 
substituting $at$ for $a$ and $bt$ for $b$ in the RHS of the Law of Cosines,
lets you facter out a $t^2$ from the expressions for $c^2$. In other 
words, the $RHS(at,bt,\gamma)$ = $t^2 c^2 = (ct)^2 $. Hence the third 
side is multiplied by the same factor. 

Now make the same subsitution in $ b^2 = c^2 + a^2 -2ca\cos(\beta)$.
We may not assume that $\beta$ remains the same. We are about to prove that.
So, making the subsitution and using the previously proven fact for $c$,
we get $ t^2 b^2 = t^2(c^2 + a^2 -2ca \cos(\beta')$. Cancelling the $t^2$ and 
comparing the equation to the Law of Cosines, the only possible conclusion
is that $ \cos(\beta) = \cos(\beta')$. Since the cosine is 1:1 over the 
range $0 .. \pi$, we get that the angle is unchanged. 

The identical argument applied to the third angle proves simSAS. 

\subsection{Algebraic proof of the Law of Cosines.}
There is a misprint, the LHS should be a lower case $c$. The important issue here is that using
vector notation, we multiply the expression out ``as usual", but careful to interpret multiplication
as the dot product. Of coures, you should use the fact $ UV = |U||V|\cos\angle(U,V) $.

\subsection{Birkhoff's Protractor Postulate}

The solution of this problem is written out in complete detail in Hvidsten. 
But because we plan to treat it as part of the geometry of complex numbers,
Birkhoff's Protractor Axiom is not on the midterm.

\section{Advice for the Essay Questions}
There will be questions requiring roughly 30 minutes of essay-type answers.
(On the final, an hour is scheduled for the essays.)
You may prepare these ahead of time, and put them into your Journal, at 
least in outline form so you won't have to make them up entirely on 
the test. 

You should prepare short but good answers to such questions like 
``What is Absolute Geometry", "What is non-Euclidean Geometry? " etc.
Be sure you have definitions of various 
technical terms we use handy in your journal. When you review, don't just
read, transfer what you read from the the input side of your brain to the
output side by writing something into your journal.

The principle to follow on the midterm is to tell me clearly what you know,
and don't try to fake what you don't know. You don't have to know everything
perfectly. But if you attempt to sneak around the question by simply stating
the conclusion of a proof without adequate justification, you will actually
have points taken off.

Your answers must make sense to anyone reading your answer. But since it is
a test, it suffices to describe any theorem you use in a proof in the briefest
terms, including nicknames like "Playfair" etc. But do not cite page numbers
or other identifiers to the text or notes just because you have it in your 
Journal. The grader is under no obligation to "look stuff up" for you. 

\subsection{Figures}
A figure, provided it is plausibly accurate, and properly labelled, can be 
used instead of a lengthy paragraph defining all the terms you use. But if
you do neither, then a reader who is unfamiliar with the lessons and the
discussions in the course cannot tell what you are talking about. And the 
solution cannot be given full credit. 

You might practice doing some of the constructions we have done with 
the tools you'll have available: a triangle ruler and a compass (review
the Advice pages). Be sure right angles look right, and squares don't 
look like parallelograms.

If a question refers to a construction in GEX, use your memory of such 
constructions to answer it. At the very least you might review what straight
lines (LINES) look like in the various models we have studied.

\subsection{Partial Credit}
Do not take the common approach by college students that if you produce a 
brain-dump on the page, some of it will by chance be correct and earn 
partial credit. Irrelevant facts or nonsense will subtract, just as sensible
contributions to a correct answer will add to the partial credit.

\textbf{ Think before your write, but write what you think. }

\subsection{Examples}
It is appropriate on an exam on which you can use a journal to ask
for examples without explicitly identifying them. Classify the entries
in your journal, so you can answer a question like this: ``Give an 
example of a theorem in Euclidean geometry which is false in absolute geometry."

But be prepared to justify your answer. To simply guess ``The Pythagorean 
Theorem" is a correct answer, but I have no way of knowing that you know 
why. You would do better with ``Playfair's Postulate", or "the sum of 
the angles of a triangle add to $\pi$." But I still want to know why.
It would suffice to observe that, being equivalent to Euclid's 
Parallel Postulate, they are false
in hyperbolic (a.k.a. non-Euclidean) geometry, and theorems in absolute
geometry are true in both.

\section{Last Words}
You are not expected to finish the exam. But do not waste time on items you
cannot answer quickly. Above all \textbf{don't panic} as Douglas Adams advised.
And remember, even though the midterm does count towards the final grade, the 
final still counts (at least) 30pc of the total. 

\end{document}