Last edited 3apr15. Revised with thanks to Tony Winkler, 28jul11, Zheyuan Fan, 29jul11, and Saman Moniri, 31jul13.
\section{Introduction}
Of all the rigid motions, \texit{translation} surely is the most fundamental. At
the earliest age, a child is applauded when she moves one object from
here to there. Rotations and reflections come much later. Euclid recognized
this by his second Postulate, namely that a given line segment may be
\textit{prolonged} (in both directions) indefinitely into an \text{infinite
line}.
The Greeks had an aversion of using the notion of infinity, in part because it
was controversial. Even today, poorly instructed school children misinterpret
that word infinity as the name of a very large number, as in million, billion,
trillion, gazillion, infinity. No wonder they feel embarrassed when the teacher
forbids them to ask why $\infity +1 $ isn't any bigger. If for no other reason,
learning the calculus is a intelligent requirement of every educated person.
However, the Greeks would have been quite happy with an alternative word for
an infinite line, namely an \textit{unbounded line}.
Recall that in the very first construction in this course, the one leading
to a proof of the Absolute Exterior Angle Theorem, we used this concept.
In this lesson we learn which of the hyperbolic transformations come closest
to our intuitive understanding of translations. A \textit{hyperbolic
translation} turn out to be the negative of an involution, which is the
rotation of an involution about the origin by $180^o$. Hence every hyperbolic
transformation can also be written as a rotated translation.
Thus, the rule that every Euclidean motion is the composition of rotation
with a translation (careful, the order matters) persists also in
nonEuclidean geometry.
We will compare Euclidean tranlation with hyperbolic translation,
discovering many similarities, but also some significant differences.
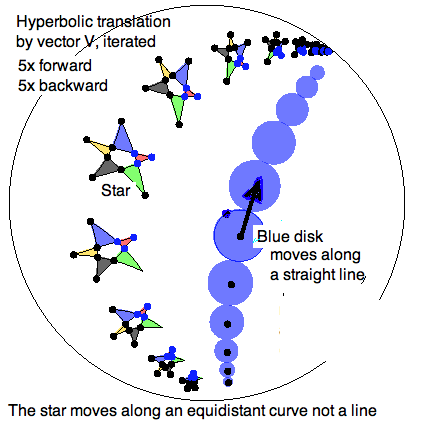
In particular, by looking at what I like to call the
\textit{Saccheri Railroad} we will lay to rest once and for all the
persistent misconception that to be parallel, lines should be equidistant
from each other. Indeed, this property is entirely Euclidean. In the
hyperbolic plane, equidistant curves cannot both be hyperbolic lines.
\section{Hyperbolic Translations}
\textbf{Denition of an hTranslation:}
\[ T_\alpha = \frac{z+\alpha}{\bar{\alpha}z +1} , \, |\alpha|<1 .\]
Observe the similarity of this definition with that of an involution in a
prior lesson. Indeed
Lesson on Hyperbolic Translations
$\C$ 2010, 2015 Prof. George K. Francis, Mathematics Department, University of Illinois. \begin{document} \maketitle
\section{Introduction}
Of all the rigid motions, \texit{translation} surely is the most fundamental. At
the earliest age, a child is applauded when she moves one object from
here to there. Rotations and reflections come much later. Euclid recognized
this by his second Postulate, namely that a given line segment may be
\textit{prolonged} (in both directions) indefinitely into an \text{infinite
line}.
The Greeks had an aversion of using the notion of infinity, in part because it
was controversial. Even today, poorly instructed school children misinterpret
that word infinity as the name of a very large number, as in million, billion,
trillion, gazillion, infinity. No wonder they feel embarrassed when the teacher
forbids them to ask why $\infity +1 $ isn't any bigger. If for no other reason,
learning the calculus is a intelligent requirement of every educated person.
However, the Greeks would have been quite happy with an alternative word for
an infinite line, namely an \textit{unbounded line}.
Recall that in the very first construction in this course, the one leading
to a proof of the Absolute Exterior Angle Theorem, we used this concept.
In this lesson we learn which of the hyperbolic transformations come closest
to our intuitive understanding of translations. A \textit{hyperbolic
translation} turn out to be the negative of an involution, which is the
rotation of an involution about the origin by $180^o$. Hence every hyperbolic
transformation can also be written as a rotated translation.
Thus, the rule that every Euclidean motion is the composition of rotation
with a translation (careful, the order matters) persists also in
nonEuclidean geometry.
We will compare Euclidean tranlation with hyperbolic translation,
discovering many similarities, but also some significant differences.
In particular, by looking at what I like to call the
\textit{Saccheri Railroad} we will lay to rest once and for all the
persistent misconception that to be parallel, lines should be equidistant
from each other. Indeed, this property is entirely Euclidean. In the
hyperbolic plane, equidistant curves cannot both be hyperbolic lines.
\section{Hyperbolic Translations}
\textbf{Denition of an hTranslation:}
\[ T_\alpha = \frac{z+\alpha}{\bar{\alpha}z +1} , \, |\alpha|<1 .\]
Observe the similarity of this definition with that of an involution in a
prior lesson. Indeed
Question 1.
Show that \[ T_\alpha (z) = - V_{-\alpha}(z) .\]
Question 2.
Given $|\alpha| < 1$ and angle $\theta$, find $|\omega|<1$ and
angle $\psi$ so that
\[ e^{i\theta}V_\alpha(z) = e^{i\psi}T_\omega(z). \]
Question 3.
Show that
\begin{eqnarray*}
\mbox{ While }T_\alpha(0) &=& \alpha \\
\mbox{ and } T_\alpha(-\alpha) &=& 0 \\
\mbox{ BUT } T_\alpha(\alpha) &=& 2\alpha \frac{2\alpha}{1+|\alpha|^2} \\
\end{eqnarray*}
To compute an explicit form for the inverse of a translation we have
two choices of how to proceed. We can solve $ w= \frac{z+\alpha}{\bar{\alpha}z+1 $
directly for $z = \frac{w-\alpha}{-\bar{\alpha}w+1}$, or avoid the
simple algebra and apply previously discovered properties of rotated
involutions. The latter is a good review, but the former is quicker here.
We can also calculate that the two fixed points of translation are the two
points, $ \pm \alpha/|\alpha}$ where the diameter through $\alpha$ meets
the unit circle. Thus $T_\alpha$ has no fixed \textit{hyperbolic points}
Finally, one should really reserve the term "translation" for a transformation
that is defined by its taking any point to some other point, not just $0 \mapsto \alpha$.
\textit{Definition Translation from Here to There}
\[ T_{\alpha, \omega} =
T_\beta \circ T_\alpha^{-1} (z) = T_\beta \circ T_{-\alpha} (z) \]
Compare this to the definition of a Euclidean translation in terms of
vectors. So we begin to see the similarities Eucldean and
nonEuclidean translations, but are beginning to suspect some
differences.
\end{document}