Revised 4feb15, with thanks to Ki Yeun Kim and Tony Winkler
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction}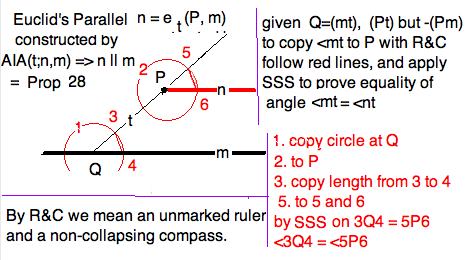
In this lesson we will study Euclid's parallel postulate and a number of
alternative axioms which historically, were suggested either as substitutes,
or even as easier to deduce from the rest of absolute geometry. Each of
these later turned out to be equivalent to Euclid's parallel postulate, given
the theorems of absolute geometry.
Before we go further, we first need some precise notation so as to avoid
tricky verbal arguments, so sort that lawyers and philosophers prefer, and
which students (and instructors) find hard to understand. Two theorems in
absolute geometry stand out in their importance here. We have already met
and discussed the absolute exterior angle theorem (AXAT). And the second
is Euclid's Propositions 28, which involves a concept we refer to as
\textit{Euclid's Line }. But first a bit of notation and a look at what
happens before Proposition 28..
\section{ Antecedents for Euclid's Parallel }
Let us look at Euclid's first postulate more closely. It says two things,
that for any two points there exists a line through them, and that this
line is unique. The uniqueness permits us to invent the notation $(PQ)$
or $\ell_{PQ}$ for \textbf{that} line which joins the two (distinct) points.
Often, we rename this line by writing $ h =(PQ)$.
Let us abbreviate the statement that $P$ is on the line $\ell$ by $P\ell$.
Then this notation can also be read that line $\ell$ goes through point $P$.
What about two lines, what is $(hk)$ ? Suppose the two lines do have
a point in common, $(\exists P)(Ph \and Pk) $. Could there be another?
No, argues Euclid went as follows:
If there were $Qh \and Qk$ there there would be two lines joining the
same two points, which contradicts Postulate 1. So, if there is such
a point, it is unique, and we write it $(hk)$. If there is no such point,
we have a new word for it, we say the two lines are \textit{parallel}, and
write it as $h \parallel k$. We could save ourselves a notation and use
$\neg(hk)$ since it says that there is no such common point. But it's easier
on the brain to write $h \parallel k$. And its negation $\neg(h \parallel k)$
just says that $hk$ meet at a single point.
Next, let's have a look at right angles. Postulate 4 is not stated in a
very enlightening way. Whatever Euclid might have meant by it, we know
that that he prized the property of two lines to be \textit{perpendicular},
which we (try) to write as $h \perp k$. We find two propositions
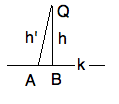\textbf{Proposition 11} $(Pk) \implies (\exists h)( hP \and h \perp k )$
\textbf{Proposition 12} $\neg(Qk) \implies (\exists h)( hQ \and h \perp k )$
That the perpendicular dropped from a point $Q$ not on a line $k$ is unique
follows from the AXAT.
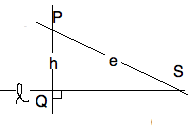Suppose $\neg (P\ell)$, we have point not on a line. Drop the perpendicular
$h$ from $P$ to $\ell$. So
$ hP \and h\perp \ell$, and we call $Q = (h\ell)$. Now erect the perpendicular,
$ eP \and e \perp (PQ) $. We use the AXAT to show that $ e \parallel \ell$.
For suppose it intersects $ S=(e\ell)$, then we have a contradiction to AXAT.
For, the $\angle SPQ $ cannot both be equal to and smaller than a
right angle. Since Euclid's parallel exists and is unique, we shall
use the notation $ e(P,\ell)$. Of course, this notation would not make
sense unless $\neg P\ell$. So, if we say that $ h=e(Q,k)$ we imply
that $Q$ does not line on $k$.
But we have a more general way of constructing a parallel through a point
not on a line. This time we are given $\net P\ell \wedge T\ell$, and
consider the line $t = (PT)$. The situation above is a special case of this,
$ T=Q \and t=h $, because it also assumes that $h \perp \ell$. We
dispense with this assumption by thinking of $T$ roaming along the entire
line it is on. You should draw a picture of this situation.
Next copy the angle $\angle \ell \t $ to $P$. We always read this angle as
oriented from $\ell$ to $t$. Of course there are two such angles, but they are
equal because the are one of the two pairs of opposite angles made when two
line cross. The copied angle also has two legs (all angles do), say $k$ so
that $ kP \wedge \angle kt = \angle \ell t$. An argument like the one above
for the case this angle is a right angle (which we don't assume now) says that
the line $k \parallel \ell$. We shall call denote this line by
$ k = e_t(P \ell ) $
and refer to it as \textit{Euclid's parallel relative to the transverse} $t$.
What we cannot guaratee in absolute geometry is that at a given point $\net P\ell$ that different Euclid's parallels are all the same line. For to be true,
Euclide realized he needed his Parallel Postulate, and we shall see why by
doing some experiments in a hyperbolic model later.
\section{Alternate Interior Angles and all that ... }
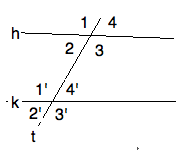Euclid's fifth postulate is phrased in terms of a \textedit{transversal} line
$t$ to two given lines $h,k$, meaning that $ (ht) \and (kt) $. The figure
immediately produces eight angles. By the \textit{Vertical Angle Theorem}
(Proposition 15) we have that all even pairs are equal, and all odd pairs
are equal. So the real question boils down to whether or not any angle is
equal to it's corresponding (primed) angle, or not. For if one pair of
corresponding angles are equal, all corresponding pairs are. Morever,
adjacent angles are \textit{supplementary}. So another equivalent condition
is for ``interior angles on the same side", $1',2$ for example, are or are
not supplementary. You can amuse yourself by finding all the possible ways
of expressing this condition using ``supplementary" in instead of ``equal".
High school geometry teachers delight in mucking around in this jungle of
possbile ways of saying the ``same thing", and thereby missing the whole
point. (So do college geometry teachers, by the way.)
\textbf{Definition:} We will abbreviate this condition with the
abbreviation $ AIA(t;h,k) $ to mean that the transvserval $t$ of
$h,k$ has any one of the above equivalent angle properties, and read it
as the \textit{Alternate Interior Angle} property for the transversal
$t$ of lines $h,k$. Aren't you glad for notational abbreviations!
The final two theorems of Euclid's absolute geometry, Propositions 27 and
28, just say that $ AIA(t;h,k) \implies h \parallel k $. Here is a
proof contradiction.
For, suppose, on the contrary, $\neg h \parallel k $, i.e. $ S = (hk)$.
Then $t,h,k$ form a $\triangle HKS$, where $H=(th), K=(tk)$.
The XAT then leads to a contradictions to $AIA(t;h,k)$.
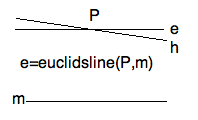The most popular formulation of Euclid's Parallel Postulate today is due to
Playfair. It says that, through a point $P$ not on a line $m$, $ \neg (Pm)$,
there is exactly one line through $P$ and parallel to $m$, or
\textbf{ Playfair: } $ \neg(Pm) \implies (\exists !\ h)( (Ph) \ \wedge\ h \parallel m) .$
But, since we already know that Euclid's parallel $e(P,m)$ exists,
we can reformulate Playfair to:
\textbf{ Playfairer: } $ \neg (Pm) \implies ( (hP) \ \wedge \ h \parallel m) \implies h = e(P,m) ) $
Using using the logical equivalence
$ (A \implies (B \implies C)) \equiv ((A \and B) \implies C) $ we can put
Playfair into an a single if-then statement which involves Euclid's parallel.
Indeed, using the generalized Euclid paralell, we can reformulate once
more.
\textbf{ Playfairest: }
$ (\neg (Pm) \and (Mm) \and t=(PM) \and (hP) \and (h \parallel m) ) \implies h = e_t(P,m) ). $
\subsection{ Proof that the Euclid5 $\implies$ Playfair.}
So consider $\neg Pf$. Draw any transverse $tP \and (tf)$. By the
contrapositive of the Fifth Postulate, if $hP$ and $ h \parallel f$ then
$AIA(t;h,f)$. This says that $h = e_t( P, f)$. In particular for
$t \perp f$, $h = e(P,f)$. So all of these parallels are the
same line, the Euler parallel to $f$ through $P$ .
\subsection{Proof that Playfair $\implies$ Euclid5 }
Given $t,h,k$ with $H=(th)$ and $K = (tk) $. There is always
$e = e_t( K,h)$ which is parallel to $h$. If $h \parallel k$ then by
Playfair, $ h= e_t(K,h)$, in other words, $AIA(t;h,k)$. So we
have just proved the contrapositive of Euclid5.
\subsection{The Proof in the Pudding}
For this section you should review your notes for the prerequisites
for this course, for example MA347. In the first section of this course,
on Euclid's Geometry, there is a short remediation which may be adequate
for present purposes.
To show that Euclid's and Playfair's versions said exactly the same thing,
we were obliged to prove what looks like a very complicated theorem of the
form
\begin{eqnarray*}
(H_1 \implies C_1) & \implies & ( H_2 \implies C_2) \\
\end{eqnarray*}
where $H_i$ is the hypothesis, and $C_i$ is the conclusion
of Euclid's ($i=1$) and Playfair ($i=2$).
And, we then proved its converse.
Recall that the following lines are logically equivalent
\begin{eqnarray*}
A \implies (B \implies C) \\
\neg A \ \or \ ( \neg B \or C) \\
(\neg A \ \or \ \neg B ) \or C \\
\neg( A \ \and \ B) \or C \\
( A \and B) \implies C \\
\end{eqnarray*}
Applying this to the triple implication above we followed this
strategy. Keep the $A = (H_1 \implies C_1$ intact, complete with
with its quantifiers. Let $B = H_2$ but establish it first. Label
its geometrical objects and consider them as given. Now find a
situation inside the given geometrical arrangments which $A$ can
be applied to. I.e. replace any fully quantified, so-called dummy
variables in $A$ with the letters from $B$.
\textbf{ Proof Strategy }
\begin{itemize}
\item To show that: if $ H_2 \and (H_1 \implies C_1)$ then $C_2$ holds.
\item Consider $H_2$ as given.
\item Apply $(H_1 \implies C_1)$ to the case of $H_2$.
\item In order to conclude that $C_2$ is true.
\end{itemize}
\subsection{Five Problems on the subject}
These problems will be assigned separately, and come with a discussion of how best to prove them.
In the meantime, you should at least translate the notation into words and draw some figures.
Playfair is equivalent to three more ways of formulating the Parallel Postulate.
\begin{itemize}
\item \textbf{0. Perp. Proclus or PPP} $ (h \parallel k \and t \perp h \and (tk)) \implies t \perp k$
\item \textbf{1. Proclus or PROC} $ (h \parallel k \ \and \ (th) ) \implies (tk) $.
\item \textbf{2. Euclid 30 or TRANS} $ (h \parallel k \ \and \ k \parallel \ell) \implies (h = \ell \or h \parallel \ell) $.
\item \textbf{3. Euclid 32 or EXAT} The exterior angle of a triangle is the sum of the opposite interior angles.
\end{itemize}
\subsection{ Discussion}
There is a subtlety in 0. Proclus' postulate for perpendiculars (PPP)if you
leave out the assumption that $(tk)$. Namely (PPP'):
\[ h \parallel k \and t \perp h \implies t \perp k\].
When it comes to proving that PPP is
equivalent to Playfair's Axiom it starts to matter. One solution to this
problem might be to include the concept of intersection when we speak of
two lines being perpendicular.
In other words, we define
\[ t\perp k \equiv (tk)\wedge \angle(tk)= 90^o.\]
But this is a bad idea for the following reason. In the Euclidean plane,
a line $t\perp m$ automatically crosses every other except another
perpendicualr to $m$, in particular every line $k \parallel m$. In
the non-Euclidean plane, however, this is not necessarily true. You'll need
to check a hyperbolic model to persuade yourself of this. Of course, Proclus
did not know this, nor even suspected it as later geometers began to do once
they studies Euclid's Fifth Postulate.
The last in this list (3) is known as the \textit{Euclidean Exterior Angle Theorem } EXAT, which
is, of course, equivalent to the \textit{Euclidean Angle Sum Theorem}
which says that the sum of the (interior) angles of a triangle is $\pi$.
Once you have written proofs that each of these four propositions are equivalent
to Plaifair into your journal (this will take you some time) then you will have
understood this lesson, Note that you have to effectively prove eight triple
implications using the above strategy. We will discuss strategies for doing this
in future lessons.
The Parallel Postulate
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction}
In this lesson we will study Euclid's parallel postulate and a number of
alternative axioms which historically, were suggested either as substitutes,
or even as easier to deduce from the rest of absolute geometry. Each of
these later turned out to be equivalent to Euclid's parallel postulate, given
the theorems of absolute geometry.
Before we go further, we first need some precise notation so as to avoid
tricky verbal arguments, so sort that lawyers and philosophers prefer, and
which students (and instructors) find hard to understand. Two theorems in
absolute geometry stand out in their importance here. We have already met
and discussed the absolute exterior angle theorem (AXAT). And the second
is Euclid's Propositions 28, which involves a concept we refer to as
\textit{Euclid's Line }. But first a bit of notation and a look at what
happens before Proposition 28..
\section{ Antecedents for Euclid's Parallel }
Let us look at Euclid's first postulate more closely. It says two things,
that for any two points there exists a line through them, and that this
line is unique. The uniqueness permits us to invent the notation $(PQ)$
or $\ell_{PQ}$ for \textbf{that} line which joins the two (distinct) points.
Often, we rename this line by writing $ h =(PQ)$.
Let us abbreviate the statement that $P$ is on the line $\ell$ by $P\ell$.
Then this notation can also be read that line $\ell$ goes through point $P$.
What about two lines, what is $(hk)$ ? Suppose the two lines do have
a point in common, $(\exists P)(Ph \and Pk) $. Could there be another?
No, argues Euclid went as follows:
If there were $Qh \and Qk$ there there would be two lines joining the
same two points, which contradicts Postulate 1. So, if there is such
a point, it is unique, and we write it $(hk)$. If there is no such point,
we have a new word for it, we say the two lines are \textit{parallel}, and
write it as $h \parallel k$. We could save ourselves a notation and use
$\neg(hk)$ since it says that there is no such common point. But it's easier
on the brain to write $h \parallel k$. And its negation $\neg(h \parallel k)$
just says that $hk$ meet at a single point.
Next, let's have a look at right angles. Postulate 4 is not stated in a
very enlightening way. Whatever Euclid might have meant by it, we know
that that he prized the property of two lines to be \textit{perpendicular},
which we (try) to write as $h \perp k$. We find two propositions
\textbf{Proposition 11} $(Pk) \implies (\exists h)( hP \and h \perp k )$
\textbf{Proposition 12} $\neg(Qk) \implies (\exists h)( hQ \and h \perp k )$
That the perpendicular dropped from a point $Q$ not on a line $k$ is unique
follows from the AXAT.
Question 1.
Prove that there cannot be two different lines that are perpendicular to
a given line at a given point on the line. Hint: Here is where you can
use Euclid's 4th Postulate to good effect.
Question 2.
Prove that there cannot be two different lines that are perpendicualr to
a given line from a point outside the line. Hint: Develop an argument
which shows that if, on the contrary, there two such lines, they would
constitute a counterexample to AXAT.
\section{Euclid's Parallel}
Suppose $\neg (P\ell)$, we have point not on a line. Drop the perpendicular
$h$ from $P$ to $\ell$. So
$ hP \and h\perp \ell$, and we call $Q = (h\ell)$. Now erect the perpendicular,
$ eP \and e \perp (PQ) $. We use the AXAT to show that $ e \parallel \ell$.
For suppose it intersects $ S=(e\ell)$, then we have a contradiction to AXAT.
For, the $\angle SPQ $ cannot both be equal to and smaller than a
right angle. Since Euclid's parallel exists and is unique, we shall
use the notation $ e(P,\ell)$. Of course, this notation would not make
sense unless $\neg P\ell$. So, if we say that $ h=e(Q,k)$ we imply
that $Q$ does not line on $k$.
But we have a more general way of constructing a parallel through a point
not on a line. This time we are given $\net P\ell \wedge T\ell$, and
consider the line $t = (PT)$. The situation above is a special case of this,
$ T=Q \and t=h $, because it also assumes that $h \perp \ell$. We
dispense with this assumption by thinking of $T$ roaming along the entire
line it is on. You should draw a picture of this situation.
Next copy the angle $\angle \ell \t $ to $P$. We always read this angle as
oriented from $\ell$ to $t$. Of course there are two such angles, but they are
equal because the are one of the two pairs of opposite angles made when two
line cross. The copied angle also has two legs (all angles do), say $k$ so
that $ kP \wedge \angle kt = \angle \ell t$. An argument like the one above
for the case this angle is a right angle (which we don't assume now) says that
the line $k \parallel \ell$. We shall call denote this line by
$ k = e_t(P \ell ) $
and refer to it as \textit{Euclid's parallel relative to the transverse} $t$.
What we cannot guaratee in absolute geometry is that at a given point $\net P\ell$ that different Euclid's parallels are all the same line. For to be true,
Euclide realized he needed his Parallel Postulate, and we shall see why by
doing some experiments in a hyperbolic model later.
\section{Alternate Interior Angles and all that ... }
Euclid's fifth postulate is phrased in terms of a \textedit{transversal} line
$t$ to two given lines $h,k$, meaning that $ (ht) \and (kt) $. The figure
immediately produces eight angles. By the \textit{Vertical Angle Theorem}
(Proposition 15) we have that all even pairs are equal, and all odd pairs
are equal. So the real question boils down to whether or not any angle is
equal to it's corresponding (primed) angle, or not. For if one pair of
corresponding angles are equal, all corresponding pairs are. Morever,
adjacent angles are \textit{supplementary}. So another equivalent condition
is for ``interior angles on the same side", $1',2$ for example, are or are
not supplementary. You can amuse yourself by finding all the possible ways
of expressing this condition using ``supplementary" in instead of ``equal".
High school geometry teachers delight in mucking around in this jungle of
possbile ways of saying the ``same thing", and thereby missing the whole
point. (So do college geometry teachers, by the way.)
\textbf{Definition:} We will abbreviate this condition with the
abbreviation $ AIA(t;h,k) $ to mean that the transvserval $t$ of
$h,k$ has any one of the above equivalent angle properties, and read it
as the \textit{Alternate Interior Angle} property for the transversal
$t$ of lines $h,k$. Aren't you glad for notational abbreviations!
The final two theorems of Euclid's absolute geometry, Propositions 27 and
28, just say that $ AIA(t;h,k) \implies h \parallel k $. Here is a
proof contradiction.
For, suppose, on the contrary, $\neg h \parallel k $, i.e. $ S = (hk)$.
Then $t,h,k$ form a $\triangle HKS$, where $H=(th), K=(tk)$.
The XAT then leads to a contradictions to $AIA(t;h,k)$.
Question 3.
If $AIA(t;h,k)$ but $S=(hk)$ then which version of AIA is violated?
Refer to the notation $H=(th)$ and $K=(tk)$. Be sure you draw a
figure when you put this into you Journal as well.
\subsection{High School Construction}
In high school you learned how to
draw parallels by copying angles along any transversal. Given a line $h$
and a point $K$ not on $h$, choose a line $t$ through $H$ that crosses
$h$ at $H$. If you copy the angle $\angle ht$ to $K$ to get $\angle kt$,
then $k \parallel h$ because $AIA(t;h,k)$. Since $k$ depends on $t$ we denote
this parallel by $e_t(K,h)$. In high school geometry, given $\neg hK$,
it didn't make any difference which transversal was used, it always
gave the same parallel. That you can do this is Euclid's Proposition 31.
But this is not the case in absolute geometry,
because you can show it to be false in a hyperbolic model. (Do it!)
\section{Summarizing }
A word on terminaoloty and its notation. The AIA property is an assertion about
the position of three lines; it is a predicate $AIA(t;h,k)$. Euclid's
parallel is a line, a geometrical object.
The \textit{Alternate Interior Angle} proposition (Euclid's Prop. 28)
is a sentence with subject and predicate. Recall, however, all the
other "equal" or "supplementary" angle relations are also asserted
by AIA, since they are all equivalent.
It is asserted for three given lines. We write $AIA(t;h,k)$, distinguishing
the transversal $t$ from the other two lines. But Euclid's
parallel $e(K,h)$, when the line from $K$ to $h$ is understood to
be the perpendicular, or $e_t(K,h)$ when it is not necessarily
perpendicular, is again a line. In absolute geometetry, these are
lines parallel to the given line $h$ and pass through a point $K$ not
on it. Of course, the two notations are related.
We have two ways of expressing the same situation
regarding three lines:
\begin{eqnarray*}
AIA(t;h,k) &\equiv& (k = e_t( (kt), h)) \\
AIA(t;h,k) &\equiv& (k = e_t( (kt), k)) \\
\end{eqnarray*}
In English, two lines and a line transversal to them have the AIA property
if and only if each line is Euclid's parallel to the other relative
to the given transversal. (Aren't you glad we have a notation to
replace such English sentences?)
We proved
\textbf{Proposition 28:} $AIA(t;h,k)\implies h \parallel k$,
by applying AXAT to its
\textbf{Contrapositive of 28:} $ \ \neg (h\parallel k) \implies \neg AIA(t;h,k)$.
Euclid was unable to prove the converse of Proposition 28, which says
\textbf{Converse 28:} $ \ h\parallel k \implies AIA(t;h,k)$.
But Euclid hoped to be more convincing by
postulating the
\textbf{Inverse 28:} $ \ \neg AIA(t;h,k) \implies \neg h \parallel k $,
and this is (very nearly) the statement of his Fifth Postulate.
In the postulate, he specifies on which side of the transversal the
non-paralle lines will meet when AIA is false.
futureFilecard: Can you prove that the inverse of a proposition is the
contrapositive of its converse. (It's time you have internalized these
concepts.)
Once we examine a few hyperbolic models we
will appreciate the fact that the
\textbf{ Negation of Converse 28 :} $(\exists h\ne k)(h \parallel k \
\wedge \ (\exists t=trans(h,k))( \negAIA(t;h,k))$
reigns in non-Euclidean geometry. Since the converse of 28 is
Euclid's fifth postulate, henceforth denoted by E5
In the second half of this lesson, we will examine Playfair's rewording
of E5.
See also Evelyn Lamb's easy to read Scientific American article on he subject.
Part II
\section{Playfair} \subsection{Historical Note 4feb15} Here is another good time to remember the facts already discussed earlier. For over two millenia mathematicians tried to prove Euclid's parallel postulate from the other four of his postulates. This was known early on to be a useless effort, but it was not known until the 19th century why they were right. Other geometers thought up other ideas for a postulate added to Euclid's from which the parallel postulate follows as theorem. They were more successful in this, but time and time again, either their proof was discovered to be incorrect, or someone showed that Euclid's postulate in turn implied the alternative; the two were equivalent. They were equivalent within absolute geometry. That means, simply accept everything Euclid wrote up to and including Propositions 28, and then show the equivalence follows. Note the equivalence doesn't prove anything more that that. Again, it took until the 19th century to discover that Euclid's parallel postulate and all of its "absolutely" equivalent formulations were \texbf{independent} of absolute geometry. That means you could accept the postulate (and get Euclidean geometry) or you could accept its negetion (and get non-Euclidean geometry). How can that be? How can something and its negation be equally "true"? Stay tuned. \subsection{Statement of Playfair's Axiom}
The most popular formulation of Euclid's Parallel Postulate today is due to
Playfair. It says that, through a point $P$ not on a line $m$, $ \neg (Pm)$,
there is exactly one line through $P$ and parallel to $m$, or
\textbf{ Playfair: } $ \neg(Pm) \implies (\exists !\ h)( (Ph) \ \wedge\ h \parallel m) .$
But, since we already know that Euclid's parallel $e(P,m)$ exists,
we can reformulate Playfair to:
\textbf{ Playfairer: } $ \neg (Pm) \implies ( (hP) \ \wedge \ h \parallel m) \implies h = e(P,m) ) $
Using using the logical equivalence
$ (A \implies (B \implies C)) \equiv ((A \and B) \implies C) $ we can put
Playfair into an a single if-then statement which involves Euclid's parallel.
Indeed, using the generalized Euclid paralell, we can reformulate once
more.
\textbf{ Playfairest: }
$ (\neg (Pm) \and (Mm) \and t=(PM) \and (hP) \and (h \parallel m) ) \implies h = e_t(P,m) ). $
\subsection{ Proof that the Euclid5 $\implies$ Playfair.}
So consider $\neg Pf$. Draw any transverse $tP \and (tf)$. By the
contrapositive of the Fifth Postulate, if $hP$ and $ h \parallel f$ then
$AIA(t;h,f)$. This says that $h = e_t( P, f)$. In particular for
$t \perp f$, $h = e(P,f)$. So all of these parallels are the
same line, the Euler parallel to $f$ through $P$ .
\subsection{Proof that Playfair $\implies$ Euclid5 }
Given $t,h,k$ with $H=(th)$ and $K = (tk) $. There is always
$e = e_t( K,h)$ which is parallel to $h$. If $h \parallel k$ then by
Playfair, $ h= e_t(K,h)$, in other words, $AIA(t;h,k)$. So we
have just proved the contrapositive of Euclid5.
\subsection{The Proof in the Pudding}
For this section you should review your notes for the prerequisites
for this course, for example MA347. In the first section of this course,
on Euclid's Geometry, there is a short remediation which may be adequate
for present purposes.
To show that Euclid's and Playfair's versions said exactly the same thing,
we were obliged to prove what looks like a very complicated theorem of the
form
\begin{eqnarray*}
(H_1 \implies C_1) & \implies & ( H_2 \implies C_2) \\
\end{eqnarray*}
where $H_i$ is the hypothesis, and $C_i$ is the conclusion
of Euclid's ($i=1$) and Playfair ($i=2$).
And, we then proved its converse.
Recall that the following lines are logically equivalent
\begin{eqnarray*}
A \implies (B \implies C) \\
\neg A \ \or \ ( \neg B \or C) \\
(\neg A \ \or \ \neg B ) \or C \\
\neg( A \ \and \ B) \or C \\
( A \and B) \implies C \\
\end{eqnarray*}
Applying this to the triple implication above we followed this
strategy. Keep the $A = (H_1 \implies C_1$ intact, complete with
with its quantifiers. Let $B = H_2$ but establish it first. Label
its geometrical objects and consider them as given. Now find a
situation inside the given geometrical arrangments which $A$ can
be applied to. I.e. replace any fully quantified, so-called dummy
variables in $A$ with the letters from $B$.
\textbf{ Proof Strategy }
\begin{itemize}
\item To show that: if $ H_2 \and (H_1 \implies C_1)$ then $C_2$ holds.
\item Consider $H_2$ as given.
\item Apply $(H_1 \implies C_1)$ to the case of $H_2$.
\item In order to conclude that $C_2$ is true.
\end{itemize}
\subsection{Five Problems on the subject}
These problems will be assigned separately, and come with a discussion of how best to prove them.
In the meantime, you should at least translate the notation into words and draw some figures.
Playfair is equivalent to three more ways of formulating the Parallel Postulate.
\begin{itemize}
\item \textbf{0. Perp. Proclus or PPP} $ (h \parallel k \and t \perp h \and (tk)) \implies t \perp k$
\item \textbf{1. Proclus or PROC} $ (h \parallel k \ \and \ (th) ) \implies (tk) $.
\item \textbf{2. Euclid 30 or TRANS} $ (h \parallel k \ \and \ k \parallel \ell) \implies (h = \ell \or h \parallel \ell) $.
\item \textbf{3. Euclid 32 or EXAT} The exterior angle of a triangle is the sum of the opposite interior angles.
\end{itemize}
\subsection{ Discussion}
There is a subtlety in 0. Proclus' postulate for perpendiculars (PPP)if you
leave out the assumption that $(tk)$. Namely (PPP'):
\[ h \parallel k \and t \perp h \implies t \perp k\].
When it comes to proving that PPP is
equivalent to Playfair's Axiom it starts to matter. One solution to this
problem might be to include the concept of intersection when we speak of
two lines being perpendicular.
In other words, we define
\[ t\perp k \equiv (tk)\wedge \angle(tk)= 90^o.\]
But this is a bad idea for the following reason. In the Euclidean plane,
a line $t\perp m$ automatically crosses every other except another
perpendicualr to $m$, in particular every line $k \parallel m$. In
the non-Euclidean plane, however, this is not necessarily true. You'll need
to check a hyperbolic model to persuade yourself of this. Of course, Proclus
did not know this, nor even suspected it as later geometers began to do once
they studies Euclid's Fifth Postulate.
The last in this list (3) is known as the \textit{Euclidean Exterior Angle Theorem } EXAT, which
is, of course, equivalent to the \textit{Euclidean Angle Sum Theorem}
which says that the sum of the (interior) angles of a triangle is $\pi$.
Once you have written proofs that each of these four propositions are equivalent
to Plaifair into your journal (this will take you some time) then you will have
understood this lesson, Note that you have to effectively prove eight triple
implications using the above strategy. We will discuss strategies for doing this
in future lessons.