Similarity and the simSAS Axiom
\textit{$\C$ 2010, 2011, 2015 Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} 17feb15 \maketitle
\section{Introduction}
This lesson is about the similiarity of figures, which refers to that property
of two geometric figures by which differ only by a change of scale (possibly
up to a translation or rotation.) Except when the two figures are actually
congruent (the scale factor is 1), similarity is a strictly Euclidean property.
Since we wish to motivate the choice of an axiom on similarity,
it is appropriate that our exposition is \textit{reductive} rather
that \texti{deductive}. We start with an application of a theorem,
and work backwards until we settle on the axiom. That is, we begin
with the familiar ruler and compass division of a segment into equal parts.
This is an practical application of the Angle-Angle-Angle (AAA) criterion
for similarity of triangles.
In an attempt to prove the AAA theorem in absolute geometry, we find a
counterexample in a hyperbolic model of non-Euclidean geometry. But, we
also find that AAA can be proved by assuming the \textit{Ladder Lemma}(LL)
and the rest of absolute geometry. A special case of LL was seen to be false
in non-Euclidean geometry.
Euclid proved the Ladder Lemma somewhere after he introduced the Parallel
Postulate (Where?). But it's proof is quite difficult if done rigorously.
As we discussed in the previous chapter on absolute geometry, the SAS
congruence theorem suffers from the same defect, and was adopted early on
as an axiom by nineteenth century geometers. But don't forget, SAS belongs
to absolute geometry; it is true in both Euclidean and non-Euclidean planes.
And here again, we show that LL follows easily from the Birkhoff's
fourth axiom, \textit{simSAS}.
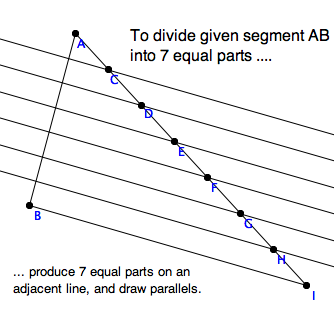
\section{Segment Division}
One of the most useful construction you (should have) learned in high school
geometry is to divide a given segment $AB$ into an arbitrary
number, $n$, of equal parts. Here is how it works.
You drew a ray from one endpoint, and marked off $n$ equal parts along the
ray, with your compass, or a strip of paper with a mark on it. Say the last
point is $N$. Then the parallels to $\ell_{BN}$ through the points cut $AB$
into $n$ equal parts.
Later, certainly by \textit{Algebra II}, you learned that all real numbers
can be approximated by rational numbers to an arbitrary degree of accuracy.
So, the question is whether you can construct an arbitrary fraction,
$\frac{n}{d}$ of a
given segment. And now you know the answer is yes. You multiply a given
segment the numerator number of times by producing the segment. You divide
the result into the denominator number of equal segments by drawing parallels.
This concept will be made extraordinarily precise in Birkhoff's \textit{Ruler
Axiom}.
FILECARD: Explain how to divide a given segment into $\frac{5}{3}$ equal parts.
\subsection{Definition of Similarity}
We shall say two triangles are \textit{similar}, $\triangle ABC \sim \triangle A'B'C' $,
if the angles are pairwise equal and corresponding sides have the same
ratio: $ \frac{|AB|}{|A'B'|} =\frac{|BC|}{|B'C'|} =\frac{|CA|}{|C'A'|}$.
\subsection{Segment division is Euclidean}
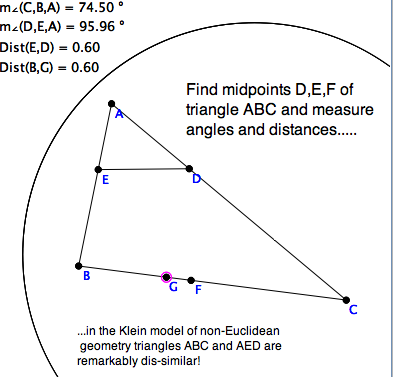The construction is definitively Euclidean. Suppose that in a hyperbolic
model we want to halve a given segment $AB$ in this way. We pick an
arbirary segment $AD$ on a different ray $A$ and double it to $AC$. We
complete $\triangle ABC$, and ... The next step is to choose a line
through $D$ and parallel to $BC$. But which one?
There are many parallels to $BC$ through $D$ in non-Euclidean geometry. You might first try Euclid's parallel obtained by copying $\angle C$ along the transverse $(AC)$. Let $E$ be where this line crosses the other side, $AB$. But why
does it cross? Because of the picture? That's what Euclid assumed, but actually,this is \textit{Peano's Axiom of Separation.} It says that there are no
holes that $(ED)$ could sneak through without crossing $AB$.
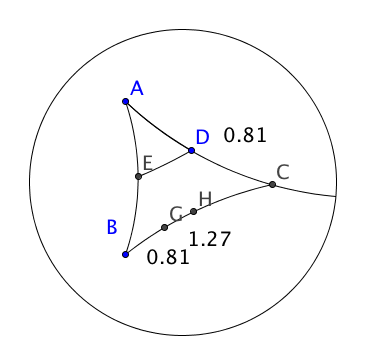Even so, there is no guarantee that $E$ is the midpoint of $AB$, which we
expected it to be. Indeed, suppose we skip the tedium of compying an angle,
and choose $E$ to be the midpoint. Then laying off the length $|ED|=|BG|$
on the base won't get us to the midpoint $F$ of $BC$. You can try to wiggle
the figure in your construction to see if you can ever get $G$ on top of $F$.
So, we conjecture from our experiment, that similarity is not part of
absolute Geometry; it must be Euclidean. Download this GGB file,
ladderlemma.ggb,
to experiment with GeoGebra.
\section{AAA criterion for Similarity}
In high school geometry, you learned that SAS, ASA, and SSS are criteria
for two triangles to be congruent. You also learned that AAA guarantees
only similarity, not congruence. Let's see next how this AAA theorem
reduces, in absolute geometry, to the \textit{Ladder Lemma}, which be
base on our previous experiment. It failed in non-Euclidean geometry, so
maybe it's true in Euclidean geometry.
\subsection{Ladder Lemma}
\textbf{Lemma:}
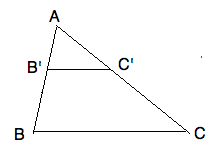If, in a $\triangle ABC$ chord $B'C'$ is drawn parallel to
base $BC$ then $\triangle ABC \sim \triangle AB'C'$. In particular
$|AB'|/|AB| =|AC'|/|AC| =|B'C'|/|BC|$.
We won't try to prove prove the Ladder Lemma here. Let's first see if it
is worthy of our efforts. We show that
\textbf{Corollary:}
The Ladder Lemma implies AAA is true in absolute geometry.
\textbf{Proof of the Corollary.}
So, suppose triangles $\triangle ABC $
and $\triangle A"B"C"$ have correspondingly labeled angles equal. If
a pair of sides are equal, say $|AB|=|A"B"|$ then we have ASA and the
two triangles are congruent. So the side ratio is 1:1 all around. ASA
is a theorem in absolute geometry.
Next, suppose that $|AB| > |A"B"|$, then we can lay off $B'$ on $AB$ so that
$|A"B"| = |AB'|$. This is a theorem in absolute geometry.
Question 1: Locate and identify which of Euclid's propositions says you
can lay off the shorter length off the longer length.
By assumption, $\angle A = \angle A"$, so we can reconstruct
$\triangle A"B"C"$ at $\triangle AB'C'$ where $C'$ lies on $(AC)$
somewhere. You can't assume anything about where on the ray $AC$ the
point $C'$ is located. For now, put it between $A$ and $C$. But
later, redraw a figure where $C$ is between $A$ and $C'$ and check that
our argument is still valid.
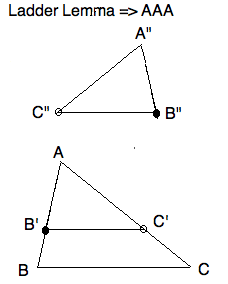By assumption, $\angle C'B'A = \angle CBA $. Therefore by Proposition
28, $ \ell_{BC} \parallel \ell_{B'C'}$. And we have reached the situation
given in the \textit{Ladder Lemma.}
\section{The simSAS Axiom}
Since we have experimental evidence that the Ladder Lemma is false in
non-Euclidean geometry, the Ladder Lemma must have a strong Euclidean
component. In other words, its proof must require a
consequence of Euclid's Parallel Postulate. The proof of the
Ladder Lemma is actually quite difficult and we will instead deduce it
from another statement, simSAS, which is a special case of LL.
As we noted above, geometers long ago noticed
that a generalization of SAS to similar triangles was extremely versatile
for proving all sorts of theorems in Euclidean geometry, including
the Ladder Lemma.
\subsection{Statement of the simSAS Axiom }
\textit{For two triangles, if two pairs of sides have the same ratio,
and the included angles are equal, then the triangles are similar.}
Note that Euclid's Proposition 4 (SAS) is a special case, the ratio in
question is 1:1. In fact, simSAS is so versatile, that George Birkhoff
adopted it as one of his only four axioms for Euclidean geometry.
\subsection{The Ladder Lemma follows from simSAS}
We must start with the hypotheses of the Ladder Lemma. To use simSAS, we
must also insure that the hypotheses of simSAS are indeed satified. So
we have some work to do. But note the resemblance of this proof to Pappus'
proof of Pons Asinorum.
The included angles, being the same, are equal.
One pair of sides simply has a particular ratio, $|AB'|/|AB|$. To show
that the other ratio, $|AC'|/|AC|$ is the same, we could assume it is different,
and aim for a contradiction. Let's be clever. Let's simply not draw the
rung of the ladder at first, and place $C'$ so that the ratio is the same on
right as on the left. Then, simSAS says that the two triangles are similar.
In particular $\angle AC'B' = \angle ACB$.
But then, by the \textit{alternate interior angle} (AIA) version of
Proposition 28, $\ell_{B'C'} \parallel \ell_{BC}$.
Now we (finally) use Euclid's Parallel Postulate in Playfair's version,
and see that the rung of the ladder we originally drew
parallel to the base, and the rung of the ladder we constructed to fulfill
the hypotheses of simSAS must be one and the same. And we've proved the
Lemma.
Question 2: Have you understood this proof and put it into your Journal?
\subsection{An Exercise on SAS}
I hope the above argument has raised your suspicions that somehow Playfair
was really necessary here. Indeed, simSAS must be false in non-Euclidean
geometry. It's actually much worse than you think. It cannot even be stated
in non-Euclidean terms, since there are no similar triangles that are not
also congruent. So only the SAS form of simSAS makes sense there. And,
SAS is a theorem in absolute geometry. So SAS not only makes sense in
non-Euclidean geometry, it is true there. We shall not prove SAS here.
Try to locate a proof on the web. There is one in Hvidsten.
With Hilbert, we will accept SAS as an axiom for absolute geometry and
be done with it. Of course, we would then have to show that SAS is
true in Cartesian geometry. Can you prove it?
Question 3: Have you found proofs of SAS in Cartesian geometry and put
them into your Journal?
\end{document}