Revised 1feb15
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction}
The second module of this course addresses the geometry which Euclid
of Alexandria (ca -300) created. In particular, we are concerned with
\textit{Book I} of his \texit{Elements}, which begins with his Postulates,
and ends with his proof of the Pythagorean Theorem (Propositions 47) and
its converse (Proposition 48). For the first 28 propositions, Euclid
carefully avoids using his fifth, the \textit{Parallel Postulate}.
This body of plane geometry is
known as \textit{Absolute Geometry}. Nowadays, it is also called
\textit{Neutral Geometry} because it does not takes sides on whether to
accept or reject the parallel postulate.
David Joyce, of Clark University, summarizes Euclid's Elements for your convenience. As you study this lesson, you might want to check these yourself.
It was Euclid's intention of proposing his Postulates, together with
informal definitions and common notions, as given, and to derive the
propositions logically from them. Euclid, however, made a number of
additional assumption without calling any particular attention to them.
Geometers corrected these deficiencies over the subsequent 2300 years.
The final formulation Euclid's axioms was made by David Hilbert (ca 1900).
Robert Campbells praphrase of
Hilbert's Axioms make easy reading.
In this course we will neither follow Euclid and present his proofs in
the classical progression, nor will we study Hilbert's axiomatic system
in any great detail. The former is purely of historical interest, and
the latter is far too technical and difficult for a first course in
college geometry.
We will discuss the high points of absolute geometry, giving proofs
only as needed to appreciate the Euclid's grand invention. When we
come to the great divide between absolute and Euclidean geometry,
we will study the structure of the theorems and proofs in considerable
detail.
A brief look into the Elements between Propositions 30 and 46 will be
followed by several proofs of Pythagoras' theorem. There are many more
on the WWW. (There is even one by President Garfield.)
The module will conclude with Birkhoff's very economical set of
axioms (only 4 as against Hilbert's 21) . The difference of these two axiomatic
systems is considerable. Birkhoff's axioms are built on top of the
entire edifice of real numbers and their arithmetic. Hilbert's is not.
Indeed, numbers and their arithmetic appear as objects inside Hilbert's
geometry. In other words, the axiomatic arithmetic of real numbers has a
model inside geometry.
The great achievement of Hilbert and his colleagues was to show that
geometry and arithmetic are equi-consistent. It is not necessary to
choose between them, we accept both arithmetic and geometry as equally
certain.
On the other hand, since Rene Descartes (ca 1600), we have based geometry
on the properties of the real numbers, in the form of analytic geometry,
a.k.a. \textit{Cartesian Geometry}. We will consider Birkhoff's
axioms, because there are fewer of them, and they already assume the
properties of the reals, and show that they have a model inside Cartesian
geometry.
\section{Definition of Absolute Geometry}
We will take the simplest
approach and consider all the definitions, theorems and proofs in Euclid's
Elements up to and including Proposition 28 as constituting \textit{absolute
geometry}. Another, more practical definition would be to say that any
theorem that is true in both Euclidean and Hyperbolic geometry is part
of absolute geometry. But how could we apply this second approach to
deciding whether a geometrical theorem is absolute or not?
For example, that an exterior angle of a triangle is greater than either
opposite interior angle (AXAT) is true Euclidean geometry, and in a
model of Non-Euclidean geometry, and use a geometrical construction package to tdo the relevant experiments. Or we could look into Euclid's Elements and
notice that AXAT is Proposition 16 in Euclid, and $16 \lte 28$.
We will use GGB for this purpose, but Hvidsten's GEX is actually more
suited for this purpope because he provides 3 models of hyperbolic
geometry, a model of spherical geometry, and 3 models of Euclidean geometry
for good measure.
Noet that in Euclidean geometry, there is a stronger version of this
theorem, which says that the exterior angle is actually the sum of the
opposite interior angles (EXAT). But this is false in nonEuclidean geometry,
and therefore EXAT is not absolute, it is strictly Euclidean. Can you
find the number for that proposition in Euclid's Elements? Is is larger than
28?
To repeat a central fact in this course, the \textit{Euclidean Exterior
Angle Theorem} (EXAT) says that the
exterior angle is the sum of the opposite interior angles. This is false
in hyperbolic geometry. Therefore, EXAT cannot be proved inside absolute
geometry. The last lesson of this course will reveal that the amount by
which EXAT fails in hyperbolic geometry, gives the area of the triangle.
So, how can you tell that a theorem is part of absolute geometry, or
requires the Parallel Postulate to be true? One way is to study Euclid's
Elements. Since $48>28$ we know that the Pythagorean Theorem (Prop. 48)
is not a part of absolute geometry. Another is to use a construcion
pagacke and check whether or not the theorem holds in both Euclidean
and in non-Euclidean models of geometry, then it must be and absolute theorem.
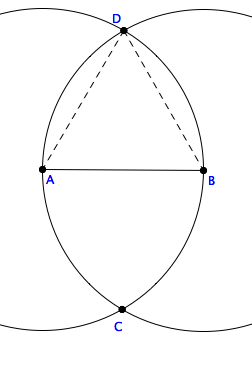Euclid's first proposition showed how to construct an equilateral triangle
on a given base AB, directly from his postulates.
By Postulate 3 we have two circles, one centered
at A and the other at B, and with the same radius.
Euclid assumed that is was obvious that
the two circles intersected at two points, C and D. In Hilbert's geometry this
was not taken for granted. It had to be proved from prior theorems. But once
we do have a point there, both dashed segments are also radii of their respective circles. Hence the triangle is equilateral.
You should remember from high school geometry, that if we now connect C and D
with a line, this becomes the perpendicular bisector of the segment AB.
\end{document}
Absolute Geometry versus Euclidean Geometry
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction}
The second module of this course addresses the geometry which Euclid
of Alexandria (ca -300) created. In particular, we are concerned with
\textit{Book I} of his \texit{Elements}, which begins with his Postulates,
and ends with his proof of the Pythagorean Theorem (Propositions 47) and
its converse (Proposition 48). For the first 28 propositions, Euclid
carefully avoids using his fifth, the \textit{Parallel Postulate}.
This body of plane geometry is
known as \textit{Absolute Geometry}. Nowadays, it is also called
\textit{Neutral Geometry} because it does not takes sides on whether to
accept or reject the parallel postulate.
David Joyce, of Clark University, summarizes Euclid's Elements for your convenience. As you study this lesson, you might want to check these yourself.
It was Euclid's intention of proposing his Postulates, together with
informal definitions and common notions, as given, and to derive the
propositions logically from them. Euclid, however, made a number of
additional assumption without calling any particular attention to them.
Geometers corrected these deficiencies over the subsequent 2300 years.
The final formulation Euclid's axioms was made by David Hilbert (ca 1900).
Robert Campbells praphrase of
Hilbert's Axioms make easy reading.
In this course we will neither follow Euclid and present his proofs in
the classical progression, nor will we study Hilbert's axiomatic system
in any great detail. The former is purely of historical interest, and
the latter is far too technical and difficult for a first course in
college geometry.
We will discuss the high points of absolute geometry, giving proofs
only as needed to appreciate the Euclid's grand invention. When we
come to the great divide between absolute and Euclidean geometry,
we will study the structure of the theorems and proofs in considerable
detail.
A brief look into the Elements between Propositions 30 and 46 will be
followed by several proofs of Pythagoras' theorem. There are many more
on the WWW. (There is even one by President Garfield.)
The module will conclude with Birkhoff's very economical set of
axioms (only 4 as against Hilbert's 21) . The difference of these two axiomatic
systems is considerable. Birkhoff's axioms are built on top of the
entire edifice of real numbers and their arithmetic. Hilbert's is not.
Indeed, numbers and their arithmetic appear as objects inside Hilbert's
geometry. In other words, the axiomatic arithmetic of real numbers has a
model inside geometry.
The great achievement of Hilbert and his colleagues was to show that
geometry and arithmetic are equi-consistent. It is not necessary to
choose between them, we accept both arithmetic and geometry as equally
certain.
On the other hand, since Rene Descartes (ca 1600), we have based geometry
on the properties of the real numbers, in the form of analytic geometry,
a.k.a. \textit{Cartesian Geometry}. We will consider Birkhoff's
axioms, because there are fewer of them, and they already assume the
properties of the reals, and show that they have a model inside Cartesian
geometry.
\section{Definition of Absolute Geometry}
We will take the simplest
approach and consider all the definitions, theorems and proofs in Euclid's
Elements up to and including Proposition 28 as constituting \textit{absolute
geometry}. Another, more practical definition would be to say that any
theorem that is true in both Euclidean and Hyperbolic geometry is part
of absolute geometry. But how could we apply this second approach to
deciding whether a geometrical theorem is absolute or not?
For example, that an exterior angle of a triangle is greater than either
opposite interior angle (AXAT) is true Euclidean geometry, and in a
model of Non-Euclidean geometry, and use a geometrical construction package to tdo the relevant experiments. Or we could look into Euclid's Elements and
notice that AXAT is Proposition 16 in Euclid, and $16 \lte 28$.
We will use GGB for this purpose, but Hvidsten's GEX is actually more
suited for this purpope because he provides 3 models of hyperbolic
geometry, a model of spherical geometry, and 3 models of Euclidean geometry
for good measure.
Noet that in Euclidean geometry, there is a stronger version of this
theorem, which says that the exterior angle is actually the sum of the
opposite interior angles (EXAT). But this is false in nonEuclidean geometry,
and therefore EXAT is not absolute, it is strictly Euclidean. Can you
find the number for that proposition in Euclid's Elements? Is is larger than
28?
To repeat a central fact in this course, the \textit{Euclidean Exterior
Angle Theorem} (EXAT) says that the
exterior angle is the sum of the opposite interior angles. This is false
in hyperbolic geometry. Therefore, EXAT cannot be proved inside absolute
geometry. The last lesson of this course will reveal that the amount by
which EXAT fails in hyperbolic geometry, gives the area of the triangle.
So, how can you tell that a theorem is part of absolute geometry, or
requires the Parallel Postulate to be true? One way is to study Euclid's
Elements. Since $48>28$ we know that the Pythagorean Theorem (Prop. 48)
is not a part of absolute geometry. Another is to use a construcion
pagacke and check whether or not the theorem holds in both Euclidean
and in non-Euclidean models of geometry, then it must be and absolute theorem.
Question 1: Do you think the theorem that rectangles have four right angles is absolutely true? Experiment with a Euclidean and a hyperbolic model in GEX. Write your results into your Journal. Report a summary here.
\section{Book I of the Elements}
Euclid invites his students to accept a long list of \textit{common notions},
which are not particularly convincing. In fact, Hilbert insisted that the primitives
of an axiomatic system are technically undefined. Of course, once you interpret
them in a model, they have a meaning. But it depends on the model you use.
Until C. F. Gauss (ca 1800) everybody, and I mean everybody was convinced that
there was only one possible geometry. And even if we humans were imperfect in
formulating this ideal geometry, it was as much there as anything we know.
What is much more interesting for us, than arguing about the nature of a point
or a line, is the tremendous care Euclid took in arranging the theorem in a
logical order. This means, none of the conclusions of a theorem was used as
the hypothesis of a prior theorem. And, almost (but not quite perfectly) he
left nothing out between a prior and a posterior proposition.
\subsection{Equilateral Triangle Theorem}
Euclid's first proposition showed how to construct an equilateral triangle
on a given base AB, directly from his postulates.
By Postulate 3 we have two circles, one centered
at A and the other at B, and with the same radius.
Euclid assumed that is was obvious that
the two circles intersected at two points, C and D. In Hilbert's geometry this
was not taken for granted. It had to be proved from prior theorems. But once
we do have a point there, both dashed segments are also radii of their respective circles. Hence the triangle is equilateral.
You should remember from high school geometry, that if we now connect C and D
with a line, this becomes the perpendicular bisector of the segment AB.
Question 2: Do you suppose this is a theorem in absolute geometry, or not?
You'll need to do some constructions in a hyperbolic model of non Euclidean
geometry to decide this experimentally.
\subsection{Side-Angle-Side Congruence}
Euclid's Proposition 4 is an attempt to prove SAS as a theorem.
Unfortunately, this one Euclid really failed to prove in any sense that
would be considered rigorous.
So we'll just accept it as another axiom, as Hilbert and most geometers do
ever since.
Question 3: Where have you seen a use of SAS in this course so far?
\subsection{Pons Asinorum}
You will recall that we really only need SAS to prove that the base angle of
an isosceles triangle are equal, Proposition 5.
Euclid, as usual, feels obliged to prove the
converse, Proposition 6.
Here, you need to be reminded just what this means. Note that every
proposition can be formulated as an if-then statement.
The proposition $H \implies C $ says that if the
\textit{hypothesis} holds then the \textit{conclusion} follows. Recall from
MA347 or its equivalent that
\begin{eqnarray*}
\mbox{the} & & \\
\mbox{proposition} & \mbox{in symbols} & \mbox{ reads } \\
& H \implies C & \mbox{ if } H \mbox{ then } C \\
\mbox{its converse} & C \implies H & \mbox{ if } C \mbox{ then } H \\
\mbox{contrapositive} & \neg C \implies \neg H & \mbox{ if not} C \mbox{ then not } H \\
\mbox{inverse} & \neg H \implies \neg C & \mbox{ if not} H \mbox{ then not } C\\
H \implies C & \mbox{ is equivalent to} & \neg H \or C \\
\neg( H \implies C) & \mbox{ is equivalent to}& H \and \neg C \\
\end{eqnarray*}
You also need to recall just why a proposition is equivalent to its
contrapositive, and similarly its converse is equivalent to its inverse.
But a proposition is not necessarily equivalent to its converse.
Question 4: State the converse of Pons Asinorum.
Question 5: State the negation of Pons Asinorum.
Can figure out a proof of the converse? A counterexample to its negation?
\subsection{What's next?}
In the next lesson we shall thoroughly study Proposition 28.
\end{document}