Z2. last edited 5mar15
Note that the numerator and the denominator have the same form, they both
are complex \textit{monomials}, i.e. polynomials of degree 1. As a
transformation, $w = az + b$ should remind you of the equation of a
straight line, $y = mx +b$ you learned in highschool. We shall study
these as a special kind of Moebius transformation, namely those for
which $c=0$ and $d=1$.
We also write the abbreviation MT for ``Moebius transformation".
Moreover, we require that a the parameters of a Moebius transformation
satisfy the condition \[ ad - bc \ne 0. \]
This eliminates from the ranks of MTs the constant functions, for example,
when $a=c=0$. But it only elimiminates the constant functions, as you
can easily prove.
of the earth to a plane, for example from the North Pole. This is a
geometric demonstration of this algebraic trick, except that on the map
there is no place for the North Pole itself. This is considered to be
that point at $\infty$ extending the plane to the sphere.
This is not an unusual mathematica process.
The complex numbers were an algebraic
extension of the reals which served, initially, the purpose of solving
quadratic equations. Geometrically, the Cartesian plane and its vectors
became a realistic picture of these numbers, just as the number line is
a convenient picture of the reals for school children.
Now, the Euclidean sphere itself has a natural group of transformations,
namely the rotations about an axis, any axis. In a later lesson we shall
study how to express rotations as MTs, and how not all MTs are rotations.
In a subsequent lesson, we shall define the hyperbolic group as the
subgroup of MT which map the unit circle into itself, the unit disk
onto itself, and therefore the exterior of the unit disk onto itself.
But, of course we want to know how to tell which MTs are hyperbolic.
Finally, there is one transformation of complex numbers we have already
met which is \textit{not} an MT, namely conjugation, $z \mapsto \bar{z}$.
Since this is the reflection of the plane in the real axis, it reverses
orientations, an angle is mapped into the negative of itself, a picture
of a left hand into a picture of a right hand. And, as we shall see
later, MT preserve orientation.
Another transformation we have already seen is inversion in a circle.
Recall that in vector form, $X \mapsto \bar{X}/|X|^2$ translates into
the transformation $z \mapsto \frac{1}{\bar{z}} $. Being a reflection,
we already knew circle inversions reverse orientation.
Lesson on Moebius Transformations of the Plane
\textit{ $\C$ 2010, 2015 Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{Introduction} In this lesson we introduce the concept of a \texit{Moebius Transformation}, which is a function on the field of complex numbers whose values can be calculated in terms of four complex parameters, $a,b,c,d$ and the arithmetic of complex numbers, \[ f : \mathbb{C} \rightarrow \mathbb{C} \mbox{ such that } f(z) = \frac{az+b}{cz+d} \]
Note that the numerator and the denominator have the same form, they both
are complex \textit{monomials}, i.e. polynomials of degree 1. As a
transformation, $w = az + b$ should remind you of the equation of a
straight line, $y = mx +b$ you learned in highschool. We shall study
these as a special kind of Moebius transformation, namely those for
which $c=0$ and $d=1$.
We also write the abbreviation MT for ``Moebius transformation".
Moreover, we require that a the parameters of a Moebius transformation
satisfy the condition \[ ad - bc \ne 0. \]
This eliminates from the ranks of MTs the constant functions, for example,
when $a=c=0$. But it only elimiminates the constant functions, as you
can easily prove.
Question 0.
Show by pure algebra that if
$ \frac{az_1 +b}{cz_1 +d}= \frac{az_2 +b}{cz_2 +d} $ but $z_1 \ne z_2$, then
$ad -bc =0$. Hint: Of course you'll need to use the field property of
Complex numbers, namely that $pq =0 \Rightarrow (p=0 \vee q=0)$
On the other hand, if we take $c=0$ but $d \ne 0$ and we are, in effect
discussing functions of the form $f(z) = a_1 z + b_1 $
where $a_1=a/d, b_1 = b/d$. We drop the subscripts.
While some authors call such Moebius transformations
by the name of \textit{similitudes}, it's not a good term because it is easily
confused with the much more general concept of similarity. An older
alternative is the adjective \textit{linear}, which is even worse because
not every linear transformation of the plane is a MT, and translations
($a = 1$) are not linear. Despite this, MTs were once
called \textit{linear fractional}. This does not seem to be a good
alternative either. So we'll call them \textit{similitudes} here .
For the case $|a| =1$, the MT becomes $f(z) = e^{i\theta}z + b$. Thus
we see that such a MT is a rotation of the plane followed by a translation.
This is called
a \textit{Euclidean Motion} or an \textit{isometry} of the plane, and
constitute the mathematical concept Euclid had in mind as the concept
of \textit{congruence}.
The plan for the lesson is to study the transformation group of
all MTs, and then certain subgroups in detail, in particular the
\textit{ Euclidean} group for the Euclidean plane, and then the
\textit{hyperbolic} group of the models of non-Euclidean geometry.
\section{Algebraic-Geometric Properties of MTs}
\subsection{Unitary Definition of a Moebius Transformation}
Also, note that the four complex numbers defining a Moebius transformaton
are by no means unique. Being a fraction, the values of the function do
not change if we replace $a,b,c,d$ by multiples of the same non-zero
complex factor. In particular, if we divide through by one of the two
squareroots of the non-zero complex number,
$\sqrt{ad-bc}$, we obtain a set of parameters for which
$a_1 d_1 - b_1 c_1 = 1$.
\subsection{Point Transformations of the Plane}
Since each complex number is the name of a point in the plane and vice
versa, we can interpret a bijection of the complex numbers as a
\textit{point transformation of the plane.} That is, each point is
transformed into a
unique other point (which may or may not be itself.)
Recall from MA347 (or the equivalent) that for a function to be \textit{bijective}
it is both 1:1 and onto.
This is a generalization from increasing (or decreasing) continuous
functions on the reals which you studied in the calculus. Since complex
numbers cannot be ordered, there is no easy way of checking that a function
is bijective.
Question 1.
Show that $f(z)=z^2$ is onto (surjective) but no 1:1 (injective). Hint:
For the former you must find at least one solution $z$
to the equation $w=z^2$ for \textit{every} $w$. For the latter it suffices to
find two different solutions for \textit{one} particular value of $w$.
\subsection{The Group of Similitudes of the Plane}
Also recall from MA347 that having an inverse functions is
the same as being a bijection. Thus similitudes are bijective,
because for every $w$, the equation$w=az+b$ can be solved uniquely for $z$.
Thus similitudes are closed under taking their inverses.
Recall also that bijections on a set form
a group under composition. The identity transformation is the compositional
identity. So, to show that the similitudes form a group it remains only to
demonstrate their closure under composition. A purely algebraic way of
doing this is to Substitute the value of the first similitude
$f_1(z) = a_1z +b_1$ into the argument of the second
$f_2(z) = a_2z +b_2$ and then simplifying $ a_2(a_1z+b)+b_2$ to look like
$f_3(z)= (f_2 \circ f_1)(z) = a_3z +b_3$. Thus similitudes are closed under
composition, and together they form a transformation group of the plane.
Question 2.
Calculate the inverse of a similitude, and then
show directly that the composition of a similitude with
its inverse is the identity.
\subsection{The Group of Moebius Transformations}
An easy computation similarly shows that the Moebius transformations form
a group (but not of the plane, as we shall see.) First, solve
$w=f(z) = \frac{az+b}{cz+d}$ for $z$ in terms of $w$, as
$z = \frac{dw-b}{-cw+a}$. Put your calculation into your Journal.
Thus $f^{-1}(z) = \frac{dz-b}{-cz+a}$ and check that $da - (-b)(-c) =1$
still. Review the introduction to recall why we need to make this check.
Question 3.
For $f(z)=\frac{az+b}{cz+d}$ and $g(z)=\frac{Az+B}{Cz+D}$, calculate
their composition $h(z)=\frac{\alpha z+\beta}{\gamma z+\delta}$ by
calculating explicitly what the parameters $\alpha, \beta, \gamma, \delta $
are in terms of $a,b,c,d,A,B,C,D$. And then show that
$\alpha \delta - \beta \gamma = 1$.
\subsection{The Extended Complex Plane}
The previous subsection illustrates how easy it is to fall into a gap in
mathematics. Nowhere did we check that every MT is a bijection of the plane.
It is not. For consider the MT with $a=b=0, b=c=0$, whose value is
\textit{multiplicative inverse} of complex number, $f(z)=\frac{1}{z}$,
more commonly called the \textit{reciprocal} of $z$. It is undefined at
$z=0$.
So we define it by adjoining one point, $\infty = \frac{1}{0}$,
to $\mathbb{C}$ to obtain the \textit{Extended Complex Plane}
$\hat{\mathbb{C}}$ and extend the arithmetic as follows.
\begin{eqnarray*}
\frac{1}{0} &=& \infty \\
\frac{1}{\infty} &=& 0 \\
\infty \pm b &=& \infty \\
\infty b &=& \infty \\
\frac{a \infty + b}{c \infty + d}&=& \frac{a}{c} \\
\end{eqnarray*}
The way to understand this strange arithmetic is, in each case, to
subsitute $\frac{1}{z}$ for each occurence $\infty$ and take the
$ \lim_{z -> 0}$. It is instructive to illustrate this method for
the last example when applying a MT to $\infty$.
\begin{eqnarray*}
\mbox{ To find: } \frac{a\infty +b }{b\infty +c} && \mbox{ substitute }\\
\frac{ a/z + b}{c/z + d} &=& \frac{a + zb}{c + zd} \\
\lim_{z->0} \frac{ a + zb}{c + zd} &=& \frac{a}{c}\\
\end{eqnarray*}
\subsection{The Moebius Group and the Special Linear Group}
Thus we can now confidently assert that the MTs form the
\textit{Moebius Group} (MG).
So far we have used only the original \textit{representation} of a MT as
$f(z) =\frac{az+b}{cz+d}, \, ad-bc=1$. If you have had matrix algebra you will
have recognized that both the inverse and composition of MTs you computed
above (you did, didn't you?)
has the same algebraic form as 2x2 matrix inverses and compositions. For example
\[\left(
\begin{array}{cc}
a & b \\
c & d \\
\end{array}
\right)^{-1}=
\left(
\begin{array}{cc}
d & -b \\
-c & a \\
\end{array}
\right)
\]
And composition becomes matrix multiplication. Thus we have a second
representation of the MG as the group of complex 2x2 matrices with unit
determinant, called the \textit{ Special Linear Group }
$SU(2,\mathbb{C})$ and important in modern physics.
\section{Geometric Properties of Moebius Transformations}
\subsection{Anatomy of a MT}
It is clear that to calculate the value of an MT all you need to know is
how to add, subtract, multiply and divide complex numbers. From a
transformational viewpoint, a MT is the composition of simpler MTs which
go by special names. We have already met similitudes, reciprocals, and
Euclidean transformations. For example, the anatomy of a similarity may
be anlyzed as follows.
Since we can write $a = re^{i\theta}$ we see that
a similitude, $f(z)= re^{i\theta} z + b $, is just the
composition of three familiar transformations, $f=f_3 \circ f_2 \circ f_1$,
where:
\begin{itemize}
\item The \textit{rotation} $ f_1(z) = e^{i\theta}z $
\item is followed by the \textit{ dilation } $ f_2(z) = rz$
\item which is followed by the \textit{ translation } $ f_3(z)= z + b$.
\end{itemize}
The functional notation is often more conveniently replaced by
the \textit{ maps-to} notation, as in
\[ z \mapsto e^{i\theta}z \mapsto r(e^{i\theta}z) \mapsto (re^{i\theta}z) + b \]
While you should have no difficulty doing a similar analysis of a MT (try
it, and put it into your Journal), a more interesting exercise is to ask
what the simplest such dissection might be. Of course ``simplest" is a matter
of taste, but the most elegant is easier to determine.
Question 4.
Verify algebraically that
\[\frac{az+b}{cz+d} = \frac{a}{c} - \frac{ad-bc}{c^2}\frac{1}{z+ d/c}\] and
conclude that every MT is the composition of a translation, followed by an
inversion, followed by a similarity. Indentify each of these three transformations.
Surely this is an elegant solution of what the anatomy of a MT is. But it also
has, as an application, a much easier, if longer, proof that the MTs form a
group. Each separate component type MTs form very familiar groups themselves.
\begin{itemize}
\item The translations are the group of vectors in the the plane.
\item The rotations (about the origin) are the group of reals modulo $2\pi$.
\item The dilations (from the origin) are the multiplicative group of positive reals.
\item The identity and inverse, $ \mathbb{Z}_1 = \{ \iota, \,
\rho(z)=\frac{1}{z}\} $ is the group of order 2 under composition.
\end{itemize}
Since compositions of bijections of are bijections, and thus have an inverse,
so do MT without the paint of calculating it explicitly. Even the composition
theorem could be derived from this anatomical dissection. But it requires
the lemma in each case, that the composition of a MT with each one of the
four elementary transformations is again an MT. Can you prove this? Its
a good training exercise to see if you understand the above.
\subsection{The Riemann Sphere}
Originally we extended the complex numbers to $\hat{\mathbb{C}}$ by
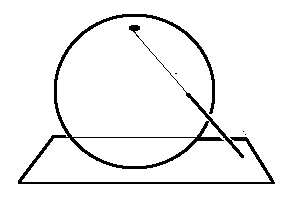
closing it up into a sphere. You may remember from high school geography,
that in addition to the familiar \textit{Mercator Projection} there is
the \textit{stereographic map projection}
of the earth to a plane, for example from the North Pole. This is a
geometric demonstration of this algebraic trick, except that on the map
there is no place for the North Pole itself. This is considered to be
that point at $\infty$ extending the plane to the sphere.
This is not an unusual mathematica process.
The complex numbers were an algebraic
extension of the reals which served, initially, the purpose of solving
quadratic equations. Geometrically, the Cartesian plane and its vectors
became a realistic picture of these numbers, just as the number line is
a convenient picture of the reals for school children.
Now, the Euclidean sphere itself has a natural group of transformations,
namely the rotations about an axis, any axis. In a later lesson we shall
study how to express rotations as MTs, and how not all MTs are rotations.
In a subsequent lesson, we shall define the hyperbolic group as the
subgroup of MT which map the unit circle into itself, the unit disk
onto itself, and therefore the exterior of the unit disk onto itself.
But, of course we want to know how to tell which MTs are hyperbolic.
Finally, there is one transformation of complex numbers we have already
met which is \textit{not} an MT, namely conjugation, $z \mapsto \bar{z}$.
Since this is the reflection of the plane in the real axis, it reverses
orientations, an angle is mapped into the negative of itself, a picture
of a left hand into a picture of a right hand. And, as we shall see
later, MT preserve orientation.
Another transformation we have already seen is inversion in a circle.
Recall that in vector form, $X \mapsto \bar{X}/|X|^2$ translates into
the transformation $z \mapsto \frac{1}{\bar{z}} $. Being a reflection,
we already knew circle inversions reverse orientation.