Lesson Z1 last edited 1mar15
\section{Introduction}
This lessons explains how, $\mathbb{C}$, the \textit{Field of Complex Numbers}
is ideally suited to describe the geometry of the Cartesian plane, just as
the field \mathbb{R} of real describes the points on a line. As everyone knows
from high school, the quadratic equation $a x^2 + b x + c =0 $ has
solution $x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$, provided that $b^2 \ge 4ac$.
Cardano (1545) discovered that the quadratic equation always has two solutions
(we count $x=0$ as a double-solution) if we admit $i = \sqrt{-1}$ as a
number. Thus $x^2+1 =0$ has the solutions $\pm i$.
Indeed, all polynomial equations has solutions in \matbb{C}. Over the subsequent
three centuries, complex numbers were fully integrated into mathematics
and its applications. Only the fact that there is no analogous way of
treating points in 3-space, where we live and do our physics, led to the
contemporary dominance of vectors over complex numbers in college. For our
present purposes we chiefly exploit the notational and conceptual efficiency of
complex numbers over 2-dimensional vector notation. In particular, the
frequent source of confusion in reading a pair, $(x,y)$ either as the point
in the Cartesian plane with coordinates $x$ and $y$, and the vector with
components $x$ and $y$ is eliminated.
\subsection{Complex numbers and 2-vectors}
We identify the point $P=(x,y)$ in the cartesian plane with the complex
number $z =x +iy$. Addition and subtraction of complex numbers is defined
to be component wise, exactly as with vectors. However, we consider the
real numbers to be part of the complex numbers.
There are two products defined for vectors, the scalar and the dot-product.
The scalar product of a vector by a real-number corresponds to the
complex product of a real and a complex number. Thus
\begin{eqnarray*}
rP = r(x,y) &= &(rx,ry) \\
\mbox{ becomes: } r(x+iy) &=& rx + iry \\
\end{eqnarray*}
As you see, multiplication looks like multiplying polynomials. Thus
\[ (x+iy)(u+iv) = xy + iyu + xiv + yv i^2 = (xy - uv)+i(xy + yv) .\]
is an algebraic computation, not an abstract rule or definition.
Vectors also have a dot product, but the dot product of two vectors
is not a vector, it is a real number. This blemish is removed as follows.
First, let us define the \textit{conjugate of a complex number } as follows:
\begin{eqnarray*}
\mbox{a complex number: } z &=& x + iy \\
\mbox{has conjugate: } \bar{z} &=& x -iy \\
\end{eqnarray*}
Next, calculate that
\[ z\bar{w} = \bar{z} w = (xu+yv) + i (xv - yu) \]
and then note that this product contains \textbf{both} products
of vectors,
\begin{eqnarray*}
\mbox{dot product: } \mathfrak{Re}(z\bar{w}) = xu+yv &=& (x,y)\cdot (u,v) \\
\mbox{determinant: } \mathfrak{Im}(z\bar{w}) = xv-yu &=&
\left|
\begin{array}{cc}
x & u \\
y & v \\
\end{array}
\right| \\
\end{eqnarray*}
Note that the two parts that make up the complext number have their own special
names, which are part of the vocabulary of the subject.
\begin{eqnarray*}
\mbox{ the complex humber: } z &=& x+iy \\
\mbox{ has real part: } \mathfrak{Re}(z) &=& x \\
\mbox{ and imaginary part: } \mathfrak{Im}(z) &=& y \\
\end{eqnarray*}
Remember both real and imaginary parts of a complex number are real numbers. They are exactly
the two components of the vector interpretation of the same point in the Cartesian plane.
\section{What you should study now.}
To become familiar with these concepts you should google various more leisurely introductions
to the subject. In addition, you can
\begin{itemize}
\item Consult Hvidsten section 4.5, pages 131 and 132. \\
\item Practice by solving Hvidsten's problems 3.5.1--3.5.5. \\
\item Study the remainder of this lesson.\\
\item Submit the filecards embedded in it.\\
\item Update your Journal for future handy reference. \\
\end{itemize}
\section{Discussion of Euler's Formula}
The best way to relate complex numbers to the Cartesian plane (which is
something you have already learned in calculus) is apply them to a new
idea due to Euler, but which containes some trigonometry you have known since
high school.
You have already seen above how scalar mutliplication by a real number is
componentwise, like addition and subtraction. Also equality of two
complext number is compnentwise in that both their real and their
imaginary parts must match. Why should multiplication be so different?
\textbf{Proof: } For consider where the
unit circle crosses the unit circle about the point 1.
By the Pythagorean theorem, it is at $ \frac{1+i\sqrt{3}}{2 $,
whose \textit{imaginary part} is irrational, hence this
point in the real Cartesian plane is not a point in the rational
Cartesian plane.
This point is missing hence in the rational Cartesian model of Euclid's
Postulates these two circles do \textbf{not} intersect.
\subsection{The surd plane and angle trisection}
On the other hand, recall that we could construct the
\textit{geometric mean} using ruler and compass. Therefore,
we can construct squareroots of by noting that $x = 1 x $.
So $\sqrt{x}$ can be constructed as the geometric mean of $1$ and $x$.
Suppose we added a square-root key to a four function calculator and
considered all possible numbers we could calculate just adding,
subtracting, multiplying, dividing and taking square-roots.
These numbers constitute the \textit{field of surd numbers}
which we'll denote by $\Sigma$.
Lesson on the Complex Plane
\textit{$\C$ 2010, 2015 Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle
\section{Introduction}
This lessons explains how, $\mathbb{C}$, the \textit{Field of Complex Numbers}
is ideally suited to describe the geometry of the Cartesian plane, just as
the field \mathbb{R} of real describes the points on a line. As everyone knows
from high school, the quadratic equation $a x^2 + b x + c =0 $ has
solution $x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$, provided that $b^2 \ge 4ac$.
Cardano (1545) discovered that the quadratic equation always has two solutions
(we count $x=0$ as a double-solution) if we admit $i = \sqrt{-1}$ as a
number. Thus $x^2+1 =0$ has the solutions $\pm i$.
Indeed, all polynomial equations has solutions in \matbb{C}. Over the subsequent
three centuries, complex numbers were fully integrated into mathematics
and its applications. Only the fact that there is no analogous way of
treating points in 3-space, where we live and do our physics, led to the
contemporary dominance of vectors over complex numbers in college. For our
present purposes we chiefly exploit the notational and conceptual efficiency of
complex numbers over 2-dimensional vector notation. In particular, the
frequent source of confusion in reading a pair, $(x,y)$ either as the point
in the Cartesian plane with coordinates $x$ and $y$, and the vector with
components $x$ and $y$ is eliminated.
\subsection{Complex numbers and 2-vectors}
We identify the point $P=(x,y)$ in the cartesian plane with the complex
number $z =x +iy$. Addition and subtraction of complex numbers is defined
to be component wise, exactly as with vectors. However, we consider the
real numbers to be part of the complex numbers.
There are two products defined for vectors, the scalar and the dot-product.
The scalar product of a vector by a real-number corresponds to the
complex product of a real and a complex number. Thus
\begin{eqnarray*}
rP = r(x,y) &= &(rx,ry) \\
\mbox{ becomes: } r(x+iy) &=& rx + iry \\
\end{eqnarray*}
As you see, multiplication looks like multiplying polynomials. Thus
\[ (x+iy)(u+iv) = xy + iyu + xiv + yv i^2 = (xy - uv)+i(xy + yv) .\]
is an algebraic computation, not an abstract rule or definition.
Vectors also have a dot product, but the dot product of two vectors
is not a vector, it is a real number. This blemish is removed as follows.
First, let us define the \textit{conjugate of a complex number } as follows:
\begin{eqnarray*}
\mbox{a complex number: } z &=& x + iy \\
\mbox{has conjugate: } \bar{z} &=& x -iy \\
\end{eqnarray*}
Next, calculate that
\[ z\bar{w} = \bar{z} w = (xu+yv) + i (xv - yu) \]
and then note that this product contains \textbf{both} products
of vectors,
\begin{eqnarray*}
\mbox{dot product: } \mathfrak{Re}(z\bar{w}) = xu+yv &=& (x,y)\cdot (u,v) \\
\mbox{determinant: } \mathfrak{Im}(z\bar{w}) = xv-yu &=&
\left|
\begin{array}{cc}
x & u \\
y & v \\
\end{array}
\right| \\
\end{eqnarray*}
Note that the two parts that make up the complext number have their own special
names, which are part of the vocabulary of the subject.
\begin{eqnarray*}
\mbox{ the complex humber: } z &=& x+iy \\
\mbox{ has real part: } \mathfrak{Re}(z) &=& x \\
\mbox{ and imaginary part: } \mathfrak{Im}(z) &=& y \\
\end{eqnarray*}
Remember both real and imaginary parts of a complex number are real numbers. They are exactly
the two components of the vector interpretation of the same point in the Cartesian plane.
\section{What you should study now.}
To become familiar with these concepts you should google various more leisurely introductions
to the subject. In addition, you can
\begin{itemize}
\item Consult Hvidsten section 4.5, pages 131 and 132. \\
\item Practice by solving Hvidsten's problems 3.5.1--3.5.5. \\
\item Study the remainder of this lesson.\\
\item Submit the filecards embedded in it.\\
\item Update your Journal for future handy reference. \\
\end{itemize}
\section{Discussion of Euler's Formula}
The best way to relate complex numbers to the Cartesian plane (which is
something you have already learned in calculus) is apply them to a new
idea due to Euler, but which containes some trigonometry you have known since
high school.
You have already seen above how scalar mutliplication by a real number is
componentwise, like addition and subtraction. Also equality of two
complext number is compnentwise in that both their real and their
imaginary parts must match. Why should multiplication be so different?
Question 1.
Prove that if the product for two complex numbers is also componentwise, i.e.
$ zw = (x+iy)(u+iv) = xu + iyv $ then one or both factors are zero,
or both must be real.
Hint: Compare the real and imaginary parts of the two products, and solve the two
equations by considering cases, using the fact that $ab=0 \implies a=0 \or b=0$
several times.
\subsection{The polar form for complex numbers.}
While multiplication of complex numbers expressed in the Cartesian format
is just a clever application of the venerable \textbf{F.O.I.L. method}
from high school:
\[ (x+iy)(u+iv)= xu + iyu + xiv + i^2 yv \]
it is not geometrically enlightening. Finally, note that we \textbf{never}
use any symbol to indicate multiplication of complex numbers. In particular,
you must \texbf{not} use $\times$ or $*$ for multiplication of complex numbers either.
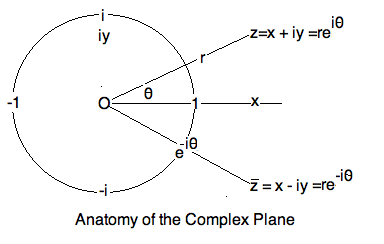
The \textit{polar form} of
a complex number, $z = re^{i\theta}$, expresses a point in the
plane in \textit{polar coordinates}. The point is a distance $r=|z|$ from
the origin, and angle $\theta=\arg(z)$ measured from the x-axis.
Thus the complex numbers $e^{i\theta}$ are exactly the points on the
\textit{unit circle}, which you are used to writing as
$(\cos\theta, \sin\theta)$. Combining these two notions, we get
\begin{eqnarray*}
\mbox{Euler's Formula :} e^{i\theta} & = & \cos \theta + i\sin\theta \\
\end{eqnarray*}
This makes complex multiplication easier and less strange.
Question 2.
Use two trigonometric identies and the definition of complex multiplication
in Cartesian form to show that
\[ (re^{i\theta})(se^{i\tau})=rse^{i(\theta + \tau)}. \]
This is one good reason for using the \textit{exponential notation} for the polar
form, as long as we agree that the imaginary exponents add under multiplication,
just like real ones. Euler had a much better reason for chosing this notation, as
we show here.
Recall the Taylor series expansion
of the exponential function applied to the term $i\theta$,
then apply the algebraic values of the powers of
$i = \sqrt{-1}$, and finally use the power series for
the sine and cosine functions to obtain this:
\begin{eqnarray*}
e^{i\theta} & = &
1 + i\theta
+ \frac{(i\theta)^2}{2!}
+ \frac{(i\theta)^3}{3!}
+ \frac{(i\theta)^4}{4!}
+ ... \\
&=&
1 + i\theta
+i^2 \frac{\theta^2}{2!}
+i^3 \frac{\theta^3}{3!}
+i^4 \frac{\theta^4}{4!}
+ ... \\
&=&
1 + i\theta
- \frac{\theta^2}{2!}
-i \frac{\theta^3}{3!}
+\frac{\theta^4}{4!}
+i\frac{\theta^5}{5!}
- \frac{\theta^6}{6!}
\pm ... \\
&=&
1 - \frac{\theta^2}{2!}
+\frac{\theta^4}{4!}
- \frac{\theta^6}{6!}
\pm ...
+i\theta
-i \frac{\theta^3}{3!}
+i\frac{\theta^5}{5!}
\pm ... \\
&=& \cos \theta + i\sin\theta \\
\end{eqnarray*}
\section{Rectangular and Polar Coordinates}
As a second application, we review the change between rectangular and polar
coordinates, but now in complex notation.
\begin{eqnarray*}
x + iy &=& \sqrt{x^2+y^2}(\frac{x}{\sqrt{x^2+y^2}} +
i\frac{y}{\sqrt{x^2+y^2}})\\
&=& r ( \cos \theta + i\sin\theta) \\
&=& r\cos \theta + i r\sin\theta \\
r &=& \sqrt{x^2+y^2} \\
\theta &=& \tan^{-1}(\frac{y}{x}) \\
x &=& r \cos\theta \\
y &=& r \sin\theta \\
\end{eqnarray*}
Question 3.
Solve $1+i = re^{i\theta}$ for $r, \theta$. Solve $x+iy=2e^{i\pi/3}$ for
$x,y$.
\section{Complex Arithmetic}
Anything named a number should have an arithmetic for solving equations, at the very
least. In fact, we should also be able to do complex analysis, including the
differentiation and integration of complex valued functions of complex variable. We
will not do the latter in this course, however much it belongs here. Vectors, you
will remember, can't be divided. There is no vector division. However, complex
multiplication has an inverse, which becomes complex division.
\subsection{Euler's Formula revisited}
The \textit{modulus} of a complex number is its distance from
the origin. Written $ |z| $, it is just the $r$ when $z=re^{i\theta}$
is written in polar form. The angle $\theta$ is called
the \textit{argument} of the complex number $ \arg z $.
Thus, we can dispense with both the Cartesian and polar coordinates
and write
\textbf{Euler's Formula}
\begin{eqnarray*}
z & = & |z| e^{i \arg z } \\
zw & = & |z||w| e^{i (\arg z + \arg w) } \\
\end{eqnarray*}
To be fair to the Cartesian form of a complex number $z=x+iy$,
we have names \textit{ real part, imaginary part} of $z$,
namely $ x = \Re{z}$ and $y = \Im{z}$, so that we can get rid
of $x,y$ too with $ z = \mathfrak{Re} (z) + i \mathfrak{Im}(z) $.
\section{Rotations and Translations}
We are, however, more interested in the geometrical significance of
complex arithmetic. With the two equivalent forms of writing complex numbers we
can write the two Euclidean transformations in the plane,
rotation and translation, in a very compact form.
\textbf{Euclidean Transformation Theorem} \\
The \textit{translation} of the entire plane by a vector $m$ takes
every point $z$ to $z + m$. The \textit{rotation} of the
entire plane by an angle $\theta$
about the origin takes every point $z$ to $e^{i\theta} z$.
\textbf{Proof: } \\
Only the second assertion deserves a proof. Note that
\begin{eqnarray*}
e^{i\theta} z &=&
e^{i\theta} |z| e^{i\arg z} \\
&=&
|z| e^{i(\theta + \arg z)} \\
\end{eqnarray*}
which clearly moves $z$ along the circle $ r=|z|$ by an
angle of $\theta$, which is what we claimed.
Question 4.
Show that multiplying a complex number by $i$ the same as rotating about the
origin by $90^o$. Give a geometrical reason that $i^4=1$.
\subsection{Rotation about an arbitrary point.}
If you want to calculate the rotation of the plane about an
arbitrary center $c$, not necessarily the origin, we first
translate the plane so that $c$ moves to the origin, rotate,
and move the plane back by inverse translation. Call this
transformation $f(z)$ and calculate:
\begin{eqnarray*}
f(z)& =& (z - c)e^{i\theta} + c \\
&=& e^{i\theta}z + (1- e^{i\theta})c \\
&=& e^{i\theta}z + f(0) \\
\end{eqnarray*}
\subsection{Complex Conjugate}
The reflection of a point $z$ in the x-axis is called the
\textit{conjugate} of $z$, written
\begin{eqnarray*}
\bar{z} & = & x - iy & = & |z|e^{-i\arg z }. \\
\end{eqnarray*}
It has this important property:
\begin{eqnarray*}
z\bar{z} = (x+iy)(x-iy)=x^2 - (iy)^2 = x^2 + y^2 = |z|^2 \\
\end{eqnarray*}
Question 5.
Calculate that
\begin{eqnarray*}
\mathfrak{Re}(z) & = & \frac{z + \bar{z}}{2} \\
\mathfrak{Im}(z) & = & \frac{z - \bar{z}}{2i} \\
\end{eqnarray*}
You don't need to memorize all these identities, but you do
need to remember the vocabulary so you can re-derive them
when necessary.
\section{The Field of Surds}
This last section is a brief reprise of a central theme of the course. We began the
course with Archimedes' trisection of an angle, but not using just ruler and compass.
Or more precisely, an unmarked ruler. For with a markable ruler Archimedes trisected
every angle. We can now at least state the solution to this two millenia old problem,
even if we do not present the solution. We then showed that Euclid made more assumltions,
if tacitly, in his proof of his first proposition, the construction of an equilateral
triangle. That we can now demonstrate as incomplete.
\subsection{The rational Cartesian plane}
Note that $\mathbb{C}$
contains $\mathbb{R}$ as a subfield, which contains $\mathbb{Q}$
the rational numbers, as a subfield. Suppose we consider the subset of points in the
plane both of whose coordinates are rational, call it
$\mathbb{Q} + i\mathbb{Q}$ for short. This too is a field, but
more interesting is the geometry of this socalled \textit{rational
Cartesian plane}.
Interpreting points and lines as we did in the case of
Birkhoff's axioms, it is plausible that all five of Euclid's
postulates hold. But already Euclid's first Proposition fails.
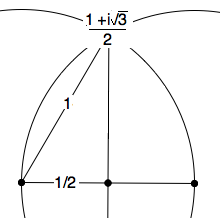
\begin{theorem}
In the rational plane, there is no equilateral triangle with
base of unit length.
\end{theorem}
\textbf{Proof: } For consider where the
unit circle crosses the unit circle about the point 1.
By the Pythagorean theorem, it is at $ \frac{1+i\sqrt{3}}{2 $,
whose \textit{imaginary part} is irrational, hence this
point in the real Cartesian plane is not a point in the rational
Cartesian plane.
This point is missing hence in the rational Cartesian model of Euclid's
Postulates these two circles do \textbf{not} intersect.
\subsection{The surd plane and angle trisection}
On the other hand, recall that we could construct the
\textit{geometric mean} using ruler and compass. Therefore,
we can construct squareroots of by noting that $x = 1 x $.
So $\sqrt{x}$ can be constructed as the geometric mean of $1$ and $x$.
Suppose we added a square-root key to a four function calculator and
considered all possible numbers we could calculate just adding,
subtracting, multiplying, dividing and taking square-roots.
These numbers constitute the \textit{field of surd numbers}
which we'll denote by $\Sigma$.
Question 6.
Show that the surds, $\Sigma$, form a subfield of the real
numbers.
Recall from MA347 that a mathematical \textit{field} is a number set
closed under addition and
multiplication, with an additive and a multiplicative identity (usually
denoted by $0,1$), and both kinds of inverses (except that $\frac{1}{0}$ is
undefined). But recall that to show something is a subfield only the closure
and existence of inverses need to be checked. The two associate laws and the
distribute law is inherited from the containing field.
In 1837, Pierre Wantzel finally settled the 2100 year old problem
of trisecting the angle, squaring the circle and doubling the
cube using (unmarked) ruler and compass alone. He showed that
the \textit{surd plane}, $\Sigma + i \Sigma$,
consisting of all points in the plane
both of whose coordinates are surds, is identical with all the
possible points that can be constructed from a unit segment using
only compass and straight-edge. Then he showed the much more difficult
theorem that trisecting certain angles (for instance with a
marked ruler, as Archimedes showed in our first lesson) could
produce an angle, one of whose sides is the real-axis (the
x-axis) and the other side has only non-surds on it (except for
the vertex.) Therefore, this angle could never be constructed by
compass and straightedge alone.
\subsection{How the ignorant world hates mathematics}
Notice the recurrence of the vulgar distaste for mathematics
which disfigures such legitimate mathematical names as
\begin{itemize}
\item \textit{negative} numbers = $\mathbb{Z} - \mathbb{N} $ \\
\item \textit{irrational} numbers = $\mathbb{R} - \mathbb{Q} $ \\
\item \textit{absurd} numbers = $\mathbb{R} - \Sigma $ \\
\item \textit{imaginary} numbers = $ i\mathbb{R} $ \\
\end{itemize}
to mean something unpleasant in the common language. Even an otherwise
neutral term, \textit{complex numbers}, is being debased by the overuse of
the adjective "complex" to mean anything halfway less banal than the obvious.
Even the word \textit{geometry} has been assigned a new, and pragmatised
meaning in computer graphics and allied fields. There it refers to anything
that does nothing more that assist computers to draw images on a computer
or device screen. But then, what used to the essence of education, the
transmission of hard won knowledge, is not nothing more than just
\textit{content}, as in calling teachers \textit{content providers.}