last edited 8feb15
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle
\section{Introduction}
In this lesson we will continue our study Euclid's parallel postulate
and its various equivalent statements.
\section{Abbreviations and Refinements}
As we have seen in the previous lesson, it is very convenient to abbreviate
a mouthful of assertions (a.k.a. conjunction of conditions) that make up
a hypothesis or a conclusion. We continue this process here to make our
later arguments more transparent.
At the left is a mnemonic, in the middle is definition, on the right is
what is being defined.
\begin{eqnarray*}
\mbox{transversal to lines: } (th) \and (tk) & \equiv & TRV(t;h,k) \\
\mbox{interior angles: } TRV(t;h,k) \and (\angle ht = \angle kt)
& \equiv & AIA(t;h,k) \\
\mbox{Euclid's parallel: } AIA(t;h,k) \and K=(tk) & \equiv & k=e_t(K;h) \\
\end{eqnarray*}
\subsection{Euclid's Fifth Postulate }
Although Euclid's formulation of Proposition 28
(the last one in absolute geometry) just states that $AIA(t;h,k)$ is a
sufficient condition for $h\parallel k $, we can now rewrite it as a much more
informative theorem:
\textbf{Proposition 28:}
\begin{eqnarray*}
\mbox{in the Elements:} AIA(t;h,k) &\implies & h\parallel k \\
\mbox{in this Course:} \{AIA(t;h,k) \and (K=(tk))\} &\implies & k=e_t(K,h) \\
\end{eqnarray*}
The converse, stated as the inverse of Proposition 28, is
\begin{eqnarray*}
\mbox{Euclid's Fifth Postulate : } \neg AIA(t;h,k) &\implies & \neg(h\parallel k) \\
\end{eqnarray*}
Recall that the contrapositive of Euclid's Fifth Postulate is just
\begin{eqnarray*}
\mbox {Fifther: } \{ h \parallel k \and TRV(t;h,k) \} &\implies & AIA(t;h,k) \\
\end{eqnarray*}
So, in view of Proposition 28, we have an even stronger form
\begin{eqnarray*}
\mbox{ Fifthest:} \{ h \parallel k \and TRV(t;h,k) \and K=(tk) \} & \implies & k=e_t(K,h) \\
\end{eqnarray*}
\subsection{Playfair's Axiom}
Recall that Playfair's Axiom is most economically expressed by
\[ PLAYF \equiv (\forall P,m )( \neg Pm \implies (\exists ! kP)( k \parallel m )) \]
But in the context of absolute geometry, we already know any number of ways of constructing
at least one such parallel, namely by using Proposition 28 to construct Euclid parallel either
by dropping a perpendicular from $P$ to $m$ or copying the angle along some other transversal.
So the existence of parallels is not the question but their uniqueness is. We also drop
writing out universal quantifiers since in mathematics we tend to assume that all variables
not specifically qualified are arbitrary and hence part of an implied universal quantification.
So we can reword Playfair's axiom more efficiently by dropping the perpendicular and write
\begin{eqnarray*}
\mbox{Playfairer } (\neg Pm \and kP \and k \parallel m ) &\implies & k = e(P,m) \\
\mbox{Playfairest } (\neg Pm \and kP \and k \parallel m \and TRV(t;m,k)\and P=(tk) &\implies & k = e_t(m,k) \\
\end{eqnarray*}
So, when should you use which form? That depends on the way you
construct the proof that Playfair is equivalent to some other
proposition in absolute geometry. The best is to review our
previous look at.
\section{ Euclid's Fifth Postulate $\implies$ Playfair's Axiom }
Here is the idea in words. From the given point off a line, drop the perpedicular and
construct Euclid's parallel. There is only one such line. Any different line passing
through the point must make an acute angle with the perpendicular. So, by Euclid's postulate,
this line isn't parallel. Hence a parallel to the line through the point exists and is unique.
\section{Playfair implies Euclid }
Again, we consider the hyposthesis of E5 as given $ TRV(t;h,k) \and \neg AIA(t,h,k)$.
There is the parallel $e=e_t(h,P)$ where $P=(tk)$ by Proposition 28 and $AIA(t,h,e)$.
So $k$ is different from $e$ and hence is not parallel to $h$. This is the conclusion
for E5 and we are done.
\section{Hints on the Assigned Problems }
\subsection{ PPP is equivalent PLAYF}
Recall the Proclus' Perpendicular Postulate (PPP) reads
\begin{eqnarray*}
\mbox{PPP:} (h \parallel k \ \and \ t \perp h \and (tk)) &\implies& t \perp k. \\
\end{eqnarray*}
Then there are two theorems to be proved here
\begin{eqnarray*}
PLAYF & \implies & PPP \\
\mbox{equivalently} (PLAYF \and h \parallel k \and t \perp h \and (tk) ) &\implies& t \perp k. \\
&\mbox{ and conversely } & \\
PPP &\implies& PLAYF \\
\mbox{namely }(PPP \and \neg(Ph) \and (kP) \and (k\parallel h)) & \implies & k=e(P,h) \\
\end{eqnarray*}
\subsection{TRANS is equivalent PLAYF}
This problem asks you to prove that parallelism, the relation
of two lines being parallel, is transitive. Do you think that
perpedicularity is a transitive relation?
Again, you should consider two implications. Euclid proved that
$TRANS \implies PLAYF$ by proving its contrapositive. For if
there is a case when two different pallels to a line cross, then
rewording this fact violates transitivity. A direct proof isn't
that different that it is difficult to word it correctly.
The converse, $PLAYF \implie TRANS$, proved by contradiction
is easier, because $\neg TRANS$ produces a figure which is
identical to the figure for $\neg PLAYF$. But it has to be
argued in the correct order.
This example shows that in some cases, both the "if" and the
"only if" are so similar that one could just use the "strong
iff" that most unmathematical people think is the same as "if".
\subsection{PROC is equivalent PLAYF}
Proclus right thought his postulate was a lot more "obvious" than
Euclid's. But nevertheless, we check it against Playfair for good
exercises. Proclus is so obvious, namely that once a line $t$ crosses
between two parallel lines, it has to cross the other.
Think of the nightmare of crossing one rail and never getting across the other rail by going straight
ahead.
\section{EXAT is equivalent PLAYF}
We started out investigation with the absolute exterior angle theorem.
We end this part with Euclid's exterior angle theorem (EXAT), which
is equivalent to the theorem every high school graduate remember from
geometry, that the sum of the interior angle of a triangle is $\pi$.
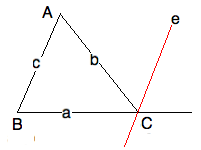By proving that EXAT is equivalent to Playfair (and therefore to
the Parallel Postulate) we see that EXAT is very ``Euclidean", but
definitely not ``absolute". Here we give a direct proof, one that
uses the E5 itself, rather than Playfair's rewording. You should,
nevertheless investigate a proof that passes directly between
Proclus and Playfair.
Let's start still in absolute geometry and draw the picture with
$e = e_b(C;c)$. Recall that $ c=(AB), b=(AC)$.
By construction, $\angle eb = \angle BAC $.
By Euclid's Fifth Postulate, $\angle ae = \angle CBA $. Done!
Well, not really done, just the end is in sight. Which aspects of
$AIA$ are we appealing to here? And, we need to conclude that
\begin{eqnarray*}
\angle A + \angle B = \angle eb + \angle ae = \angle ab \\
\end{eqnarray*}
Which is what was to be proved.
We shall not prove the converse of this theorem directly at
this time. At the completion of this lesson and its exercises
we will add a postscript taking up this question.
\section{A Matter of Efficiency}
Once you have understoof this lesson and done all the problems, you
will have written out a total of 10 proofs. But, because logical
equivalence is transitive, you will have proved 15 if-and-only-if
theorems. For instance, that $ ( EXAT \equiv PPP ) $ follows from
each of the being equivalent to Playfair..
And, if you made some logical errors along the way, or at least been
tempted to use a different equivalent property than the one needed
at the moment, then you might appreciate the logical efficiency of
proving just 6 implications. This requires that you arrange the
six theorems: E5, PLAYF, PPP, TRANS, PROC, EXAT in some, possibly different order.
And then proving that each implies the next, with the last implying the first.
This is the challenge problem for this section of the course. The writer
of this challenge does \textit{not} know the solution of this. Afterall,
just to begin with, there are 720 = 6! possible permutations to do just
the first part. Then you need to carefully construct the proofs. Some
will be easy (you can reuse proof above and on the homework, if they fit
into the scheme.)
This is definitely a group project. And we can certainly discuss your
progress in Friday labs, and online in the Moodle.
John Playfair's Parallel Axiom
\textit{$\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle
\section{Introduction}
In this lesson we will continue our study Euclid's parallel postulate
and its various equivalent statements.
\section{Abbreviations and Refinements}
As we have seen in the previous lesson, it is very convenient to abbreviate
a mouthful of assertions (a.k.a. conjunction of conditions) that make up
a hypothesis or a conclusion. We continue this process here to make our
later arguments more transparent.
At the left is a mnemonic, in the middle is definition, on the right is
what is being defined.
\begin{eqnarray*}
\mbox{transversal to lines: } (th) \and (tk) & \equiv & TRV(t;h,k) \\
\mbox{interior angles: } TRV(t;h,k) \and (\angle ht = \angle kt)
& \equiv & AIA(t;h,k) \\
\mbox{Euclid's parallel: } AIA(t;h,k) \and K=(tk) & \equiv & k=e_t(K;h) \\
\end{eqnarray*}
\subsection{Euclid's Fifth Postulate }
Although Euclid's formulation of Proposition 28
(the last one in absolute geometry) just states that $AIA(t;h,k)$ is a
sufficient condition for $h\parallel k $, we can now rewrite it as a much more
informative theorem:
\textbf{Proposition 28:}
\begin{eqnarray*}
\mbox{in the Elements:} AIA(t;h,k) &\implies & h\parallel k \\
\mbox{in this Course:} \{AIA(t;h,k) \and (K=(tk))\} &\implies & k=e_t(K,h) \\
\end{eqnarray*}
The converse, stated as the inverse of Proposition 28, is
\begin{eqnarray*}
\mbox{Euclid's Fifth Postulate : } \neg AIA(t;h,k) &\implies & \neg(h\parallel k) \\
\end{eqnarray*}
Recall that the contrapositive of Euclid's Fifth Postulate is just
\begin{eqnarray*}
\mbox {Fifther: } \{ h \parallel k \and TRV(t;h,k) \} &\implies & AIA(t;h,k) \\
\end{eqnarray*}
So, in view of Proposition 28, we have an even stronger form
\begin{eqnarray*}
\mbox{ Fifthest:} \{ h \parallel k \and TRV(t;h,k) \and K=(tk) \} & \implies & k=e_t(K,h) \\
\end{eqnarray*}
\subsection{Playfair's Axiom}
Recall that Playfair's Axiom is most economically expressed by
\[ PLAYF \equiv (\forall P,m )( \neg Pm \implies (\exists ! kP)( k \parallel m )) \]
But in the context of absolute geometry, we already know any number of ways of constructing
at least one such parallel, namely by using Proposition 28 to construct Euclid parallel either
by dropping a perpendicular from $P$ to $m$ or copying the angle along some other transversal.
So the existence of parallels is not the question but their uniqueness is. We also drop
writing out universal quantifiers since in mathematics we tend to assume that all variables
not specifically qualified are arbitrary and hence part of an implied universal quantification.
So we can reword Playfair's axiom more efficiently by dropping the perpendicular and write
\begin{eqnarray*}
\mbox{Playfairer } (\neg Pm \and kP \and k \parallel m ) &\implies & k = e(P,m) \\
\mbox{Playfairest } (\neg Pm \and kP \and k \parallel m \and TRV(t;m,k)\and P=(tk) &\implies & k = e_t(m,k) \\
\end{eqnarray*}
So, when should you use which form? That depends on the way you
construct the proof that Playfair is equivalent to some other
proposition in absolute geometry. The best is to review our
previous look at.
\section{ Euclid's Fifth Postulate $\implies$ Playfair's Axiom }
Here is the idea in words. From the given point off a line, drop the perpedicular and
construct Euclid's parallel. There is only one such line. Any different line passing
through the point must make an acute angle with the perpendicular. So, by Euclid's postulate,
this line isn't parallel. Hence a parallel to the line through the point exists and is unique.
\section{Playfair implies Euclid }
Again, we consider the hyposthesis of E5 as given $ TRV(t;h,k) \and \neg AIA(t,h,k)$.
There is the parallel $e=e_t(h,P)$ where $P=(tk)$ by Proposition 28 and $AIA(t,h,e)$.
So $k$ is different from $e$ and hence is not parallel to $h$. This is the conclusion
for E5 and we are done.
\section{Hints on the Assigned Problems }
\subsection{ PPP is equivalent PLAYF}
Recall the Proclus' Perpendicular Postulate (PPP) reads
\begin{eqnarray*}
\mbox{PPP:} (h \parallel k \ \and \ t \perp h \and (tk)) &\implies& t \perp k. \\
\end{eqnarray*}
Then there are two theorems to be proved here
\begin{eqnarray*}
PLAYF & \implies & PPP \\
\mbox{equivalently} (PLAYF \and h \parallel k \and t \perp h \and (tk) ) &\implies& t \perp k. \\
&\mbox{ and conversely } & \\
PPP &\implies& PLAYF \\
\mbox{namely }(PPP \and \neg(Ph) \and (kP) \and (k\parallel h)) & \implies & k=e(P,h) \\
\end{eqnarray*}
\subsection{TRANS is equivalent PLAYF}
This problem asks you to prove that parallelism, the relation
of two lines being parallel, is transitive. Do you think that
perpedicularity is a transitive relation?
Again, you should consider two implications. Euclid proved that
$TRANS \implies PLAYF$ by proving its contrapositive. For if
there is a case when two different pallels to a line cross, then
rewording this fact violates transitivity. A direct proof isn't
that different that it is difficult to word it correctly.
The converse, $PLAYF \implie TRANS$, proved by contradiction
is easier, because $\neg TRANS$ produces a figure which is
identical to the figure for $\neg PLAYF$. But it has to be
argued in the correct order.
This example shows that in some cases, both the "if" and the
"only if" are so similar that one could just use the "strong
iff" that most unmathematical people think is the same as "if".
\subsection{PROC is equivalent PLAYF}
Proclus right thought his postulate was a lot more "obvious" than
Euclid's. But nevertheless, we check it against Playfair for good
exercises. Proclus is so obvious, namely that once a line $t$ crosses
between two parallel lines, it has to cross the other.
Think of the nightmare of crossing one rail and never getting across the other rail by going straight
ahead.
\section{EXAT is equivalent PLAYF}
We started out investigation with the absolute exterior angle theorem.
We end this part with Euclid's exterior angle theorem (EXAT), which
is equivalent to the theorem every high school graduate remember from
geometry, that the sum of the interior angle of a triangle is $\pi$.
By proving that EXAT is equivalent to Playfair (and therefore to
the Parallel Postulate) we see that EXAT is very ``Euclidean", but
definitely not ``absolute". Here we give a direct proof, one that
uses the E5 itself, rather than Playfair's rewording. You should,
nevertheless investigate a proof that passes directly between
Proclus and Playfair.
Let's start still in absolute geometry and draw the picture with
$e = e_b(C;c)$. Recall that $ c=(AB), b=(AC)$.
By construction, $\angle eb = \angle BAC $.
By Euclid's Fifth Postulate, $\angle ae = \angle CBA $. Done!
Well, not really done, just the end is in sight. Which aspects of
$AIA$ are we appealing to here? And, we need to conclude that
\begin{eqnarray*}
\angle A + \angle B = \angle eb + \angle ae = \angle ab \\
\end{eqnarray*}
Which is what was to be proved.
We shall not prove the converse of this theorem directly at
this time. At the completion of this lesson and its exercises
we will add a postscript taking up this question.
\section{A Matter of Efficiency}
Once you have understoof this lesson and done all the problems, you
will have written out a total of 10 proofs. But, because logical
equivalence is transitive, you will have proved 15 if-and-only-if
theorems. For instance, that $ ( EXAT \equiv PPP ) $ follows from
each of the being equivalent to Playfair..
And, if you made some logical errors along the way, or at least been
tempted to use a different equivalent property than the one needed
at the moment, then you might appreciate the logical efficiency of
proving just 6 implications. This requires that you arrange the
six theorems: E5, PLAYF, PPP, TRANS, PROC, EXAT in some, possibly different order.
And then proving that each implies the next, with the last implying the first.
This is the challenge problem for this section of the course. The writer
of this challenge does \textit{not} know the solution of this. Afterall,
just to begin with, there are 720 = 6! possible permutations to do just
the first part. Then you need to carefully construct the proofs. Some
will be easy (you can reuse proof above and on the homework, if they fit
into the scheme.)
This is definitely a group project. And we can certainly discuss your
progress in Friday labs, and online in the Moodle.