H2 edited 23jul11, corrected 2aug11 with help from Tony Winkler
 \section{What you should study now.}
This lesson replaces Theorem 8.11. The remainder of Hvidsten
Section 8.2 is the same.
\section{Motivation}
In studying the Cartesian plane as a model for Euclidean geometry we discussed
Birkhoff's Ruler Axiom. Since we did not study Hvidsten's Chapter 7 to which
he refers in the proof of Theorem 8.11, we shall define a hyperbolic ruler
and its associated hyperbolic distance in terms of cross ratios. Since the
cross ratio is invariant under all Moebius transformations, it is invariant
on the subgroup of Moebius transformations we have identified as the
\textit{ hyperbolic group} of isometries in the Poincare disk model.
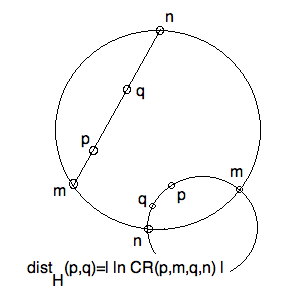
To avoid confusion with Hvidsten's exposition, which is initially different
than ours, the points in the figure here are labelled differently than
in the textbook. Note we have drawn two cases of four points. Points
$p,q$ are inside the unit disk, and $m,n$ are on on the unit
circle. In one case the four points lie on the same (Euclidean) line,
in the second, they lie on a Euclidean circle. So, in both cases they
lie on a circline.
Since the circle is drawn perpedicular to the unit circle, it is a
hyperbolic Line in the Poincare model of the hyperbolic
plane. Of course, only the circular arc minus its endpoints is the
hyperbolic Line. Because the
line on the left does not go through the origin, it is not interpreted
as a hyperbolic Line. On the other hand, if we were discussing the
Beltrami-Klein model, it would be the other way around. The chord of the
circle would be a hyperbolic Line, and the circular arc would not.
Therefore, it is best \textit{not} to make any interpretation yet,
and just continue to consider both cases where the four points lie
on the same \textit{circline}.
Recall, by the \textit{ Symmetry Principle}, four points lie on the
same circline if and only iff their cross ratio is a real number.
Because we have abbreviated the exposition of this material to
concentrate on the essentials, the Symmetry Principle is accepted
here without proof.
\section{Definition}.
Given $p,q$ inside the disk, let $m,n$ be the points where the $\ell_{pq}$
crosses the unit circle. From vector geometry we recall that there are
two real numbers $r,s$ such that
\begin{eqnarray*}
m &=& q + r(p-q) \ \mbox{with} \ r > 1 \\
n &=& p + s(q-p) \ \mbox{with} \ s > 1 \\
\end{eqnarray*}
So we can calculate directly, without knowing additional properties of
Moebius transformation, that
\begin{eqnarray*}
CR(p,m,q,n) &=& \frac{(r-1)(s-1)}{rs} > 0 \\
\end{eqnarray*}
\section{What you should study now.}
This lesson replaces Theorem 8.11. The remainder of Hvidsten
Section 8.2 is the same.
\section{Motivation}
In studying the Cartesian plane as a model for Euclidean geometry we discussed
Birkhoff's Ruler Axiom. Since we did not study Hvidsten's Chapter 7 to which
he refers in the proof of Theorem 8.11, we shall define a hyperbolic ruler
and its associated hyperbolic distance in terms of cross ratios. Since the
cross ratio is invariant under all Moebius transformations, it is invariant
on the subgroup of Moebius transformations we have identified as the
\textit{ hyperbolic group} of isometries in the Poincare disk model.
To avoid confusion with Hvidsten's exposition, which is initially different
than ours, the points in the figure here are labelled differently than
in the textbook. Note we have drawn two cases of four points. Points
$p,q$ are inside the unit disk, and $m,n$ are on on the unit
circle. In one case the four points lie on the same (Euclidean) line,
in the second, they lie on a Euclidean circle. So, in both cases they
lie on a circline.
Since the circle is drawn perpedicular to the unit circle, it is a
hyperbolic Line in the Poincare model of the hyperbolic
plane. Of course, only the circular arc minus its endpoints is the
hyperbolic Line. Because the
line on the left does not go through the origin, it is not interpreted
as a hyperbolic Line. On the other hand, if we were discussing the
Beltrami-Klein model, it would be the other way around. The chord of the
circle would be a hyperbolic Line, and the circular arc would not.
Therefore, it is best \textit{not} to make any interpretation yet,
and just continue to consider both cases where the four points lie
on the same \textit{circline}.
Recall, by the \textit{ Symmetry Principle}, four points lie on the
same circline if and only iff their cross ratio is a real number.
Because we have abbreviated the exposition of this material to
concentrate on the essentials, the Symmetry Principle is accepted
here without proof.
\section{Definition}.
Given $p,q$ inside the disk, let $m,n$ be the points where the $\ell_{pq}$
crosses the unit circle. From vector geometry we recall that there are
two real numbers $r,s$ such that
\begin{eqnarray*}
m &=& q + r(p-q) \ \mbox{with} \ r > 1 \\
n &=& p + s(q-p) \ \mbox{with} \ s > 1 \\
\end{eqnarray*}
So we can calculate directly, without knowing additional properties of
Moebius transformation, that
\begin{eqnarray*}
CR(p,m,q,n) &=& \frac{(r-1)(s-1)}{rs} > 0 \\
\end{eqnarray*}
 Now that we know the cross ratio discussed above is a positive real
number, it is in the domain of the logarithm function. Indeed, as $p$
ranges over the entire portion of the circline between $m$ and $n$ (excluding
the endpoints), it's logarithm ranges over the entire real line from
$-\infty$ to $+\infty$ (excluding the "end points", of course.) So this
fuction $ t_p = log_e(CR(p,m,q,n))$ is an excellent candidate for a
non Euclidean ruler.
\subsection{Distance}
The absolute value of the logarithm we calculated above is a positive
real number, which the distance between two points should be in any geometry.
However, the concept of distance needs to have additional properties to be
useful.
\textbf{Axioms for Distance}
\begin{eqnarray*}
(\forall p,q \in \mathbb{C} ) \ d(p,q) & \ge & 0 \\
(\forall p,q \in \mathbb{C}) \ d(p,q) &=& d(q,p) \ \mbox{symmetry} \\
(\forall p,k,q \in \mathbb{C}) \ d(p,q) & \le & d(q,k) + d(k,p) \ \mbox{triangle inquality} \\
(\forall p,q \in \mathbb{C}) \ d(p,q)= 0 & \implies & p = q \\
\end{eqnarray*}
Recall from our discussion of Birkhoff's Ruler Axiom that the rulers and
the distance have to be related. Consider the ruler on the
$\ell = circline(m,p,q,r)$.
\begin{eqnarray*}
t_\ell(z) & := & \ln CR(z,m,q,n) \\
t_\ell(m) &=& -\infty \\
t_\ell(q) &=& 0 \\
t_\ell(n) &=& +\infty \\
\end{eqnarray*}
We have taken the (natural) logarithm to stretch the reals over the
the positive and negatives. $t_\ell$ sets up a 1:1 and onto relation
between the line-segment, or circular-arc $m,q,n$ and the entire
real line, in both
cases, the end points are not included (called $\pm \infty$ as limiting
cases).
Since the ruler is defined in terms of the cross ratio, it is invariant
under Moebius transformations, in particular Moebius transformations
that have additional properties. For example those in the
hyperbolic group, which preserve the unit circle, and map the unit disk
to itself. Thus we can now rightly call the MTs of the form
\begin{eqnarray*}
f(z) &=& e^{i\theta}\frac{z - \alpha}{\bar{\alpha}z -1} \\
\end{eqnarray*}
the \textit{ isometries} in the Poincare model of non-Euclidean geometry.
These then, are the correct interpretation of the primitive notion of
\textit{ congruence} first formalized by Euclid.
\subsubsection{Comment}
Tony Winkler correctly pointed out that this section was abbreviated and
so left the reader wondering what the point was to introduce the "axioms"
for distance without further discussion. Missing is the verification that
the functions we call hyperbolic distance does, in fact, satisfy these
axioms. The first, second and fourth property are easily deduced directly
from the definition and the properties of cross-rations and logarithms.
The Triangle Inequality is more difficult to verify. Although it is one
of the exercises in Hvidsten, it will be elaborated here in a future
edition of these notes.
\subsection{How about the other two models?}
It is clear that part of the above approach, the definition of a rulers
in terms of logarithms of cross ratios, will work in the other two models.
\subsubsection{Beltrami-Klein model}
Here the Lines are chords of the unit disk.
But here, the interpretaton of "congruences" in terms of a group of
transformations is more difficult and not treated in this course.
\subsubsection{Upper Half Plane mdoel}
Here the Lines are vertical rays in the UHP, and circular arcs perpendicular
to the x-axis. Thus the Lines are again circlines. And the exact
approach applies. It is not particularly difficult to compute the canonical
form of the MTs which preserves this geometry. It turns out that we
can use the same definitions for this model as well.
However, more is true. There is a Moebius transformation which takes
the Poincare disk model into the UHP models, namely the MT which
takes $-i, 1, i$ to $0,1,\infty}. We shall discuss this issue further
in a later lesson.
\section{Calculation of Hyperbolic Distance}
We saw why \[ d_H(z_0, z_1) = | log CR(z_0,\omega_0, z_1, \omega_1)| \]
is the right choice for the distance function. We have changed the
notation once again, to make it more mnemonic. Note that the subscripts
match, so you can remember the order of the points on their circline,
namely $\omega_0, z_0, z_1, \omega_1 $.
Unfortunately, for the purpose of building
the \textit{ Geometry Explorer}, this is computationally expensive.
It requires finding the omega-points (on the unit circle)
of the Line through the two points. So Hvidsten uses a simpler formula for
computing the hyperbolic distance. In Exercise 8.2.13, Hvidsten tells
you to compute a formula which depends only on the two given points,
and does not require you to compute the omega-points on the unit
circle. The
lemma for this is Proposition 8.14, for which we give the following proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, "every point is equal!"
But in a particular model, "some points are more equal than others."
In the Poincare disk model, the origin is a very special point (though
a perfectly ordinary Point!)
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations,
we can measure distances between Points by moving their Lines into a
special position using a hyperbolic isometry. So, one way to measure
the hyperbolic distance $d_H(z_0,z_1)$ would be to first find an element
in the group which takes $z_0 \mapsto 0$ and $z_1 \mapsto r \in \mathbb{R}$,
and calculate $d_H(0,r)$. This is easier, because we know the end points
on the real diameter, namely $-1,+1$, i.e.
$d_H(0,r) = |log CR(0,-1,r,1)| $. Can you determine $r$?
\subsection{The Motion Invariance Principle (MIP)}
This idea is so important we will give it a fancy name for easier
reference. Here it is in words:
\textit{Any geometric property of a configuration of points
which is invariant (remains the same) under a hyperbolic isometry,
may be reliably investigated after the data has been moved into
a convenient position in the model.}
Note, for Euclidean geometry you have been following this principle
throughout all of your school career.
Afterall, when the teacher drew a particular figure
and then proved a property of the figure, why is this a proof for
every figure like it? She usually says something like, "without loss
of generality", or perhaps, "since we made no particular assumptions
about the points". Actually, it holds for all figures that are
congruent to the given one, by the Euclidean MIP.
In hyperbolic geometry, you have already met MIP in the discussion
of a Lambert quadrilateral $ABCD$ with right angles at $A,B,C$. If
we use a hyperbolic translation (discussed in the next section)
moving the figure so that $B \mapsto 0$ and then rotate so that
$C \mapsto c \in \mathbb{R}$, i.e. so that the new position of $C$ is
on the real axis, then $A$ will have moved to the imaginary axis.
Now the hyperblic perpendiculars at $A$ and $C$ are circular arcs
that "bend away from each other." If they do meet at $D$, it will be
at an acute angle there. Thus the angle at $D$ in the original figure
must be the same, hence also acute.
\subsection{Calculation from the definition}
Since $0, z$ lie on a diameter, it's omega points are easily computed.
Now that we know the cross ratio discussed above is a positive real
number, it is in the domain of the logarithm function. Indeed, as $p$
ranges over the entire portion of the circline between $m$ and $n$ (excluding
the endpoints), it's logarithm ranges over the entire real line from
$-\infty$ to $+\infty$ (excluding the "end points", of course.) So this
fuction $ t_p = log_e(CR(p,m,q,n))$ is an excellent candidate for a
non Euclidean ruler.
\subsection{Distance}
The absolute value of the logarithm we calculated above is a positive
real number, which the distance between two points should be in any geometry.
However, the concept of distance needs to have additional properties to be
useful.
\textbf{Axioms for Distance}
\begin{eqnarray*}
(\forall p,q \in \mathbb{C} ) \ d(p,q) & \ge & 0 \\
(\forall p,q \in \mathbb{C}) \ d(p,q) &=& d(q,p) \ \mbox{symmetry} \\
(\forall p,k,q \in \mathbb{C}) \ d(p,q) & \le & d(q,k) + d(k,p) \ \mbox{triangle inquality} \\
(\forall p,q \in \mathbb{C}) \ d(p,q)= 0 & \implies & p = q \\
\end{eqnarray*}
Recall from our discussion of Birkhoff's Ruler Axiom that the rulers and
the distance have to be related. Consider the ruler on the
$\ell = circline(m,p,q,r)$.
\begin{eqnarray*}
t_\ell(z) & := & \ln CR(z,m,q,n) \\
t_\ell(m) &=& -\infty \\
t_\ell(q) &=& 0 \\
t_\ell(n) &=& +\infty \\
\end{eqnarray*}
We have taken the (natural) logarithm to stretch the reals over the
the positive and negatives. $t_\ell$ sets up a 1:1 and onto relation
between the line-segment, or circular-arc $m,q,n$ and the entire
real line, in both
cases, the end points are not included (called $\pm \infty$ as limiting
cases).
Since the ruler is defined in terms of the cross ratio, it is invariant
under Moebius transformations, in particular Moebius transformations
that have additional properties. For example those in the
hyperbolic group, which preserve the unit circle, and map the unit disk
to itself. Thus we can now rightly call the MTs of the form
\begin{eqnarray*}
f(z) &=& e^{i\theta}\frac{z - \alpha}{\bar{\alpha}z -1} \\
\end{eqnarray*}
the \textit{ isometries} in the Poincare model of non-Euclidean geometry.
These then, are the correct interpretation of the primitive notion of
\textit{ congruence} first formalized by Euclid.
\subsubsection{Comment}
Tony Winkler correctly pointed out that this section was abbreviated and
so left the reader wondering what the point was to introduce the "axioms"
for distance without further discussion. Missing is the verification that
the functions we call hyperbolic distance does, in fact, satisfy these
axioms. The first, second and fourth property are easily deduced directly
from the definition and the properties of cross-rations and logarithms.
The Triangle Inequality is more difficult to verify. Although it is one
of the exercises in Hvidsten, it will be elaborated here in a future
edition of these notes.
\subsection{How about the other two models?}
It is clear that part of the above approach, the definition of a rulers
in terms of logarithms of cross ratios, will work in the other two models.
\subsubsection{Beltrami-Klein model}
Here the Lines are chords of the unit disk.
But here, the interpretaton of "congruences" in terms of a group of
transformations is more difficult and not treated in this course.
\subsubsection{Upper Half Plane mdoel}
Here the Lines are vertical rays in the UHP, and circular arcs perpendicular
to the x-axis. Thus the Lines are again circlines. And the exact
approach applies. It is not particularly difficult to compute the canonical
form of the MTs which preserves this geometry. It turns out that we
can use the same definitions for this model as well.
However, more is true. There is a Moebius transformation which takes
the Poincare disk model into the UHP models, namely the MT which
takes $-i, 1, i$ to $0,1,\infty}. We shall discuss this issue further
in a later lesson.
\section{Calculation of Hyperbolic Distance}
We saw why \[ d_H(z_0, z_1) = | log CR(z_0,\omega_0, z_1, \omega_1)| \]
is the right choice for the distance function. We have changed the
notation once again, to make it more mnemonic. Note that the subscripts
match, so you can remember the order of the points on their circline,
namely $\omega_0, z_0, z_1, \omega_1 $.
Unfortunately, for the purpose of building
the \textit{ Geometry Explorer}, this is computationally expensive.
It requires finding the omega-points (on the unit circle)
of the Line through the two points. So Hvidsten uses a simpler formula for
computing the hyperbolic distance. In Exercise 8.2.13, Hvidsten tells
you to compute a formula which depends only on the two given points,
and does not require you to compute the omega-points on the unit
circle. The
lemma for this is Proposition 8.14, for which we give the following proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, "every point is equal!"
But in a particular model, "some points are more equal than others."
In the Poincare disk model, the origin is a very special point (though
a perfectly ordinary Point!)
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations,
we can measure distances between Points by moving their Lines into a
special position using a hyperbolic isometry. So, one way to measure
the hyperbolic distance $d_H(z_0,z_1)$ would be to first find an element
in the group which takes $z_0 \mapsto 0$ and $z_1 \mapsto r \in \mathbb{R}$,
and calculate $d_H(0,r)$. This is easier, because we know the end points
on the real diameter, namely $-1,+1$, i.e.
$d_H(0,r) = |log CR(0,-1,r,1)| $. Can you determine $r$?
\subsection{The Motion Invariance Principle (MIP)}
This idea is so important we will give it a fancy name for easier
reference. Here it is in words:
\textit{Any geometric property of a configuration of points
which is invariant (remains the same) under a hyperbolic isometry,
may be reliably investigated after the data has been moved into
a convenient position in the model.}
Note, for Euclidean geometry you have been following this principle
throughout all of your school career.
Afterall, when the teacher drew a particular figure
and then proved a property of the figure, why is this a proof for
every figure like it? She usually says something like, "without loss
of generality", or perhaps, "since we made no particular assumptions
about the points". Actually, it holds for all figures that are
congruent to the given one, by the Euclidean MIP.
In hyperbolic geometry, you have already met MIP in the discussion
of a Lambert quadrilateral $ABCD$ with right angles at $A,B,C$. If
we use a hyperbolic translation (discussed in the next section)
moving the figure so that $B \mapsto 0$ and then rotate so that
$C \mapsto c \in \mathbb{R}$, i.e. so that the new position of $C$ is
on the real axis, then $A$ will have moved to the imaginary axis.
Now the hyperblic perpendiculars at $A$ and $C$ are circular arcs
that "bend away from each other." If they do meet at $D$, it will be
at an acute angle there. Thus the angle at $D$ in the original figure
must be the same, hence also acute.
\subsection{Calculation from the definition}
Since $0, z$ lie on a diameter, it's omega points are easily computed.
Lesson on Hyperbolic Distance
\textit{ $\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois} \begin{document} \maketitle \section{What you should study now.}
This lesson replaces Theorem 8.11. The remainder of Hvidsten
Section 8.2 is the same.
\section{Motivation}
In studying the Cartesian plane as a model for Euclidean geometry we discussed
Birkhoff's Ruler Axiom. Since we did not study Hvidsten's Chapter 7 to which
he refers in the proof of Theorem 8.11, we shall define a hyperbolic ruler
and its associated hyperbolic distance in terms of cross ratios. Since the
cross ratio is invariant under all Moebius transformations, it is invariant
on the subgroup of Moebius transformations we have identified as the
\textit{ hyperbolic group} of isometries in the Poincare disk model.
To avoid confusion with Hvidsten's exposition, which is initially different
than ours, the points in the figure here are labelled differently than
in the textbook. Note we have drawn two cases of four points. Points
$p,q$ are inside the unit disk, and $m,n$ are on on the unit
circle. In one case the four points lie on the same (Euclidean) line,
in the second, they lie on a Euclidean circle. So, in both cases they
lie on a circline.
Since the circle is drawn perpedicular to the unit circle, it is a
hyperbolic Line in the Poincare model of the hyperbolic
plane. Of course, only the circular arc minus its endpoints is the
hyperbolic Line. Because the
line on the left does not go through the origin, it is not interpreted
as a hyperbolic Line. On the other hand, if we were discussing the
Beltrami-Klein model, it would be the other way around. The chord of the
circle would be a hyperbolic Line, and the circular arc would not.
Therefore, it is best \textit{not} to make any interpretation yet,
and just continue to consider both cases where the four points lie
on the same \textit{circline}.
Recall, by the \textit{ Symmetry Principle}, four points lie on the
same circline if and only iff their cross ratio is a real number.
Because we have abbreviated the exposition of this material to
concentrate on the essentials, the Symmetry Principle is accepted
here without proof.
\section{Definition}.
Given $p,q$ inside the disk, let $m,n$ be the points where the $\ell_{pq}$
crosses the unit circle. From vector geometry we recall that there are
two real numbers $r,s$ such that
\begin{eqnarray*}
m &=& q + r(p-q) \ \mbox{with} \ r > 1 \\
n &=& p + s(q-p) \ \mbox{with} \ s > 1 \\
\end{eqnarray*}
So we can calculate directly, without knowing additional properties of
Moebius transformation, that
\begin{eqnarray*}
CR(p,m,q,n) &=& \frac{(r-1)(s-1)}{rs} > 0 \\
\end{eqnarray*}
\section{What you should study now.}
This lesson replaces Theorem 8.11. The remainder of Hvidsten
Section 8.2 is the same.
\section{Motivation}
In studying the Cartesian plane as a model for Euclidean geometry we discussed
Birkhoff's Ruler Axiom. Since we did not study Hvidsten's Chapter 7 to which
he refers in the proof of Theorem 8.11, we shall define a hyperbolic ruler
and its associated hyperbolic distance in terms of cross ratios. Since the
cross ratio is invariant under all Moebius transformations, it is invariant
on the subgroup of Moebius transformations we have identified as the
\textit{ hyperbolic group} of isometries in the Poincare disk model.
To avoid confusion with Hvidsten's exposition, which is initially different
than ours, the points in the figure here are labelled differently than
in the textbook. Note we have drawn two cases of four points. Points
$p,q$ are inside the unit disk, and $m,n$ are on on the unit
circle. In one case the four points lie on the same (Euclidean) line,
in the second, they lie on a Euclidean circle. So, in both cases they
lie on a circline.
Since the circle is drawn perpedicular to the unit circle, it is a
hyperbolic Line in the Poincare model of the hyperbolic
plane. Of course, only the circular arc minus its endpoints is the
hyperbolic Line. Because the
line on the left does not go through the origin, it is not interpreted
as a hyperbolic Line. On the other hand, if we were discussing the
Beltrami-Klein model, it would be the other way around. The chord of the
circle would be a hyperbolic Line, and the circular arc would not.
Therefore, it is best \textit{not} to make any interpretation yet,
and just continue to consider both cases where the four points lie
on the same \textit{circline}.
Recall, by the \textit{ Symmetry Principle}, four points lie on the
same circline if and only iff their cross ratio is a real number.
Because we have abbreviated the exposition of this material to
concentrate on the essentials, the Symmetry Principle is accepted
here without proof.
\section{Definition}.
Given $p,q$ inside the disk, let $m,n$ be the points where the $\ell_{pq}$
crosses the unit circle. From vector geometry we recall that there are
two real numbers $r,s$ such that
\begin{eqnarray*}
m &=& q + r(p-q) \ \mbox{with} \ r > 1 \\
n &=& p + s(q-p) \ \mbox{with} \ s > 1 \\
\end{eqnarray*}
So we can calculate directly, without knowing additional properties of
Moebius transformation, that
\begin{eqnarray*}
CR(p,m,q,n) &=& \frac{(r-1)(s-1)}{rs} > 0 \\
\end{eqnarray*}
Question 1.
Given four points $m,p,q,n$ on the same line in this order, so that
$ m = q + r(p-q), n = p + s(q-p) $ for two reals numbers $r,s$, verify
their crossratio is a real number
$CR(p,m,q,n) = \frac{(r-1)(s-1)}{rs}$.
But it is not so easy to verify that this fraction is positive directly
from the definition of the cross ratio. Here is an
alternative arguments \textit{using} geometric properties of MTs.
Note that the Moebius transformation $z \mapsto CR(z;m,q,n)$ takes
$m\mapsto 0, q\mapsto 1, n\mapsto \infty $. Therefore, it takes the point
$p$ into the interval $0 < f(p) < 1 $. So the numerator of the fraction
is the product of \textit{ two} negative real numbers.
\subsection{The case of circles}
Suppose now $m, p,q,n$ lie on a circle in that positive order. We have
showed that the Moebius transformation $f(z) := CR(z;m,q,n) $ takes
$f(m)=0, f(q) = 1, f(n)= \infty $, and it takes $circ(m,q,n)$ to
the real line, preserving order. Thus the $arc(m,q,n)$ goes to the
positive real line. The first assertion is easily recomputed from
the defition of the cross-ratio. But the second assertion is another
fact about MTs which we shall simply assume here as a lemma to be
proved elsewhere, and at another time.
\subsection{Logarithms}
 Now that we know the cross ratio discussed above is a positive real
number, it is in the domain of the logarithm function. Indeed, as $p$
ranges over the entire portion of the circline between $m$ and $n$ (excluding
the endpoints), it's logarithm ranges over the entire real line from
$-\infty$ to $+\infty$ (excluding the "end points", of course.) So this
fuction $ t_p = log_e(CR(p,m,q,n))$ is an excellent candidate for a
non Euclidean ruler.
\subsection{Distance}
The absolute value of the logarithm we calculated above is a positive
real number, which the distance between two points should be in any geometry.
However, the concept of distance needs to have additional properties to be
useful.
\textbf{Axioms for Distance}
\begin{eqnarray*}
(\forall p,q \in \mathbb{C} ) \ d(p,q) & \ge & 0 \\
(\forall p,q \in \mathbb{C}) \ d(p,q) &=& d(q,p) \ \mbox{symmetry} \\
(\forall p,k,q \in \mathbb{C}) \ d(p,q) & \le & d(q,k) + d(k,p) \ \mbox{triangle inquality} \\
(\forall p,q \in \mathbb{C}) \ d(p,q)= 0 & \implies & p = q \\
\end{eqnarray*}
Recall from our discussion of Birkhoff's Ruler Axiom that the rulers and
the distance have to be related. Consider the ruler on the
$\ell = circline(m,p,q,r)$.
\begin{eqnarray*}
t_\ell(z) & := & \ln CR(z,m,q,n) \\
t_\ell(m) &=& -\infty \\
t_\ell(q) &=& 0 \\
t_\ell(n) &=& +\infty \\
\end{eqnarray*}
We have taken the (natural) logarithm to stretch the reals over the
the positive and negatives. $t_\ell$ sets up a 1:1 and onto relation
between the line-segment, or circular-arc $m,q,n$ and the entire
real line, in both
cases, the end points are not included (called $\pm \infty$ as limiting
cases).
Since the ruler is defined in terms of the cross ratio, it is invariant
under Moebius transformations, in particular Moebius transformations
that have additional properties. For example those in the
hyperbolic group, which preserve the unit circle, and map the unit disk
to itself. Thus we can now rightly call the MTs of the form
\begin{eqnarray*}
f(z) &=& e^{i\theta}\frac{z - \alpha}{\bar{\alpha}z -1} \\
\end{eqnarray*}
the \textit{ isometries} in the Poincare model of non-Euclidean geometry.
These then, are the correct interpretation of the primitive notion of
\textit{ congruence} first formalized by Euclid.
\subsubsection{Comment}
Tony Winkler correctly pointed out that this section was abbreviated and
so left the reader wondering what the point was to introduce the "axioms"
for distance without further discussion. Missing is the verification that
the functions we call hyperbolic distance does, in fact, satisfy these
axioms. The first, second and fourth property are easily deduced directly
from the definition and the properties of cross-rations and logarithms.
The Triangle Inequality is more difficult to verify. Although it is one
of the exercises in Hvidsten, it will be elaborated here in a future
edition of these notes.
\subsection{How about the other two models?}
It is clear that part of the above approach, the definition of a rulers
in terms of logarithms of cross ratios, will work in the other two models.
\subsubsection{Beltrami-Klein model}
Here the Lines are chords of the unit disk.
But here, the interpretaton of "congruences" in terms of a group of
transformations is more difficult and not treated in this course.
\subsubsection{Upper Half Plane mdoel}
Here the Lines are vertical rays in the UHP, and circular arcs perpendicular
to the x-axis. Thus the Lines are again circlines. And the exact
approach applies. It is not particularly difficult to compute the canonical
form of the MTs which preserves this geometry. It turns out that we
can use the same definitions for this model as well.
However, more is true. There is a Moebius transformation which takes
the Poincare disk model into the UHP models, namely the MT which
takes $-i, 1, i$ to $0,1,\infty}. We shall discuss this issue further
in a later lesson.
\section{Calculation of Hyperbolic Distance}
We saw why \[ d_H(z_0, z_1) = | log CR(z_0,\omega_0, z_1, \omega_1)| \]
is the right choice for the distance function. We have changed the
notation once again, to make it more mnemonic. Note that the subscripts
match, so you can remember the order of the points on their circline,
namely $\omega_0, z_0, z_1, \omega_1 $.
Unfortunately, for the purpose of building
the \textit{ Geometry Explorer}, this is computationally expensive.
It requires finding the omega-points (on the unit circle)
of the Line through the two points. So Hvidsten uses a simpler formula for
computing the hyperbolic distance. In Exercise 8.2.13, Hvidsten tells
you to compute a formula which depends only on the two given points,
and does not require you to compute the omega-points on the unit
circle. The
lemma for this is Proposition 8.14, for which we give the following proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, "every point is equal!"
But in a particular model, "some points are more equal than others."
In the Poincare disk model, the origin is a very special point (though
a perfectly ordinary Point!)
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations,
we can measure distances between Points by moving their Lines into a
special position using a hyperbolic isometry. So, one way to measure
the hyperbolic distance $d_H(z_0,z_1)$ would be to first find an element
in the group which takes $z_0 \mapsto 0$ and $z_1 \mapsto r \in \mathbb{R}$,
and calculate $d_H(0,r)$. This is easier, because we know the end points
on the real diameter, namely $-1,+1$, i.e.
$d_H(0,r) = |log CR(0,-1,r,1)| $. Can you determine $r$?
\subsection{The Motion Invariance Principle (MIP)}
This idea is so important we will give it a fancy name for easier
reference. Here it is in words:
\textit{Any geometric property of a configuration of points
which is invariant (remains the same) under a hyperbolic isometry,
may be reliably investigated after the data has been moved into
a convenient position in the model.}
Note, for Euclidean geometry you have been following this principle
throughout all of your school career.
Afterall, when the teacher drew a particular figure
and then proved a property of the figure, why is this a proof for
every figure like it? She usually says something like, "without loss
of generality", or perhaps, "since we made no particular assumptions
about the points". Actually, it holds for all figures that are
congruent to the given one, by the Euclidean MIP.
In hyperbolic geometry, you have already met MIP in the discussion
of a Lambert quadrilateral $ABCD$ with right angles at $A,B,C$. If
we use a hyperbolic translation (discussed in the next section)
moving the figure so that $B \mapsto 0$ and then rotate so that
$C \mapsto c \in \mathbb{R}$, i.e. so that the new position of $C$ is
on the real axis, then $A$ will have moved to the imaginary axis.
Now the hyperblic perpendiculars at $A$ and $C$ are circular arcs
that "bend away from each other." If they do meet at $D$, it will be
at an acute angle there. Thus the angle at $D$ in the original figure
must be the same, hence also acute.
\subsection{Calculation from the definition}
Since $0, z$ lie on a diameter, it's omega points are easily computed.
Now that we know the cross ratio discussed above is a positive real
number, it is in the domain of the logarithm function. Indeed, as $p$
ranges over the entire portion of the circline between $m$ and $n$ (excluding
the endpoints), it's logarithm ranges over the entire real line from
$-\infty$ to $+\infty$ (excluding the "end points", of course.) So this
fuction $ t_p = log_e(CR(p,m,q,n))$ is an excellent candidate for a
non Euclidean ruler.
\subsection{Distance}
The absolute value of the logarithm we calculated above is a positive
real number, which the distance between two points should be in any geometry.
However, the concept of distance needs to have additional properties to be
useful.
\textbf{Axioms for Distance}
\begin{eqnarray*}
(\forall p,q \in \mathbb{C} ) \ d(p,q) & \ge & 0 \\
(\forall p,q \in \mathbb{C}) \ d(p,q) &=& d(q,p) \ \mbox{symmetry} \\
(\forall p,k,q \in \mathbb{C}) \ d(p,q) & \le & d(q,k) + d(k,p) \ \mbox{triangle inquality} \\
(\forall p,q \in \mathbb{C}) \ d(p,q)= 0 & \implies & p = q \\
\end{eqnarray*}
Recall from our discussion of Birkhoff's Ruler Axiom that the rulers and
the distance have to be related. Consider the ruler on the
$\ell = circline(m,p,q,r)$.
\begin{eqnarray*}
t_\ell(z) & := & \ln CR(z,m,q,n) \\
t_\ell(m) &=& -\infty \\
t_\ell(q) &=& 0 \\
t_\ell(n) &=& +\infty \\
\end{eqnarray*}
We have taken the (natural) logarithm to stretch the reals over the
the positive and negatives. $t_\ell$ sets up a 1:1 and onto relation
between the line-segment, or circular-arc $m,q,n$ and the entire
real line, in both
cases, the end points are not included (called $\pm \infty$ as limiting
cases).
Since the ruler is defined in terms of the cross ratio, it is invariant
under Moebius transformations, in particular Moebius transformations
that have additional properties. For example those in the
hyperbolic group, which preserve the unit circle, and map the unit disk
to itself. Thus we can now rightly call the MTs of the form
\begin{eqnarray*}
f(z) &=& e^{i\theta}\frac{z - \alpha}{\bar{\alpha}z -1} \\
\end{eqnarray*}
the \textit{ isometries} in the Poincare model of non-Euclidean geometry.
These then, are the correct interpretation of the primitive notion of
\textit{ congruence} first formalized by Euclid.
\subsubsection{Comment}
Tony Winkler correctly pointed out that this section was abbreviated and
so left the reader wondering what the point was to introduce the "axioms"
for distance without further discussion. Missing is the verification that
the functions we call hyperbolic distance does, in fact, satisfy these
axioms. The first, second and fourth property are easily deduced directly
from the definition and the properties of cross-rations and logarithms.
The Triangle Inequality is more difficult to verify. Although it is one
of the exercises in Hvidsten, it will be elaborated here in a future
edition of these notes.
\subsection{How about the other two models?}
It is clear that part of the above approach, the definition of a rulers
in terms of logarithms of cross ratios, will work in the other two models.
\subsubsection{Beltrami-Klein model}
Here the Lines are chords of the unit disk.
But here, the interpretaton of "congruences" in terms of a group of
transformations is more difficult and not treated in this course.
\subsubsection{Upper Half Plane mdoel}
Here the Lines are vertical rays in the UHP, and circular arcs perpendicular
to the x-axis. Thus the Lines are again circlines. And the exact
approach applies. It is not particularly difficult to compute the canonical
form of the MTs which preserves this geometry. It turns out that we
can use the same definitions for this model as well.
However, more is true. There is a Moebius transformation which takes
the Poincare disk model into the UHP models, namely the MT which
takes $-i, 1, i$ to $0,1,\infty}. We shall discuss this issue further
in a later lesson.
\section{Calculation of Hyperbolic Distance}
We saw why \[ d_H(z_0, z_1) = | log CR(z_0,\omega_0, z_1, \omega_1)| \]
is the right choice for the distance function. We have changed the
notation once again, to make it more mnemonic. Note that the subscripts
match, so you can remember the order of the points on their circline,
namely $\omega_0, z_0, z_1, \omega_1 $.
Unfortunately, for the purpose of building
the \textit{ Geometry Explorer}, this is computationally expensive.
It requires finding the omega-points (on the unit circle)
of the Line through the two points. So Hvidsten uses a simpler formula for
computing the hyperbolic distance. In Exercise 8.2.13, Hvidsten tells
you to compute a formula which depends only on the two given points,
and does not require you to compute the omega-points on the unit
circle. The
lemma for this is Proposition 8.14, for which we give the following proof:
\subsection{ Distance from the origin}
Hyperbolic geometry has no preferred points, "every point is equal!"
But in a particular model, "some points are more equal than others."
In the Poincare disk model, the origin is a very special point (though
a perfectly ordinary Point!)
Similarly for diameters, especially the one on the real axis. Since
hyperbolic distance is based on cross ratios, and cross ratios are
invariant under Moebius transformations,
we can measure distances between Points by moving their Lines into a
special position using a hyperbolic isometry. So, one way to measure
the hyperbolic distance $d_H(z_0,z_1)$ would be to first find an element
in the group which takes $z_0 \mapsto 0$ and $z_1 \mapsto r \in \mathbb{R}$,
and calculate $d_H(0,r)$. This is easier, because we know the end points
on the real diameter, namely $-1,+1$, i.e.
$d_H(0,r) = |log CR(0,-1,r,1)| $. Can you determine $r$?
\subsection{The Motion Invariance Principle (MIP)}
This idea is so important we will give it a fancy name for easier
reference. Here it is in words:
\textit{Any geometric property of a configuration of points
which is invariant (remains the same) under a hyperbolic isometry,
may be reliably investigated after the data has been moved into
a convenient position in the model.}
Note, for Euclidean geometry you have been following this principle
throughout all of your school career.
Afterall, when the teacher drew a particular figure
and then proved a property of the figure, why is this a proof for
every figure like it? She usually says something like, "without loss
of generality", or perhaps, "since we made no particular assumptions
about the points". Actually, it holds for all figures that are
congruent to the given one, by the Euclidean MIP.
In hyperbolic geometry, you have already met MIP in the discussion
of a Lambert quadrilateral $ABCD$ with right angles at $A,B,C$. If
we use a hyperbolic translation (discussed in the next section)
moving the figure so that $B \mapsto 0$ and then rotate so that
$C \mapsto c \in \mathbb{R}$, i.e. so that the new position of $C$ is
on the real axis, then $A$ will have moved to the imaginary axis.
Now the hyperblic perpendiculars at $A$ and $C$ are circular arcs
that "bend away from each other." If they do meet at $D$, it will be
at an acute angle there. Thus the angle at $D$ in the original figure
must be the same, hence also acute.
\subsection{Calculation from the definition}
Since $0, z$ lie on a diameter, it's omega points are easily computed.
Question 2.
Show does the line $\ell_{0,z}$ through $0,z$, crosses the unit circle at $\pm \frac{z}{|z|}$.
So $d_H(0,z) = log CR(0,-\frac{z}{|z|},z,\frac{z}{|z|})$ is easy to
compute from the definition.
\subsection{Using the MIP}
First, rotate the entire disk by $z \mapsto e^{-i\theta}z$, where
$\theta = \arg(z)$. This is an isometry, which takes $z$ to $r=|z|$. But
now $CR(0, -1, r, 1) = \frac{1-r}{1+r} <1$ , so the distance is
$d_H(0,r) = - \log\frac{1-r}{1+r}= \log\frac{1+r}{1-r}$ as claimed. Done.
Question 3.
What rule for logarithms were applied in showing that
$ - \log\frac{1-r}{1+r}= \log\frac{1+r}{1-r}$ ?
\subsection{General case}
The trick is to reduce the general case (Exercise 8.2.13) to the
particular case (Proposition 8.14). The hyperbolic translation
$ f(z) = \frac{z-z_0}{1-\bar{z_0}z} $ takes $z_0 \mapsto 0$. Where
must $f(z_1)$ be? Wherever it is, we can now measure its distance
to the origin and clear some fractions to get the formula
\begin{eqnarray*}
d_H(z_0,z_1) &=& \log( \frac{|1-\bar{z_0}z_1| + |z_1 - z_0|}
{|1-\bar{z_0}z_1| - |z_1 - z_0| }) \\
\end{eqnarray*}
Question 4.
Calculate the hyperbolic distance $d_H(\frac{1}{2},\frac{1}{2}i)$.