Last edited 15mar15
\begin{document} Jump to Part II \maketitle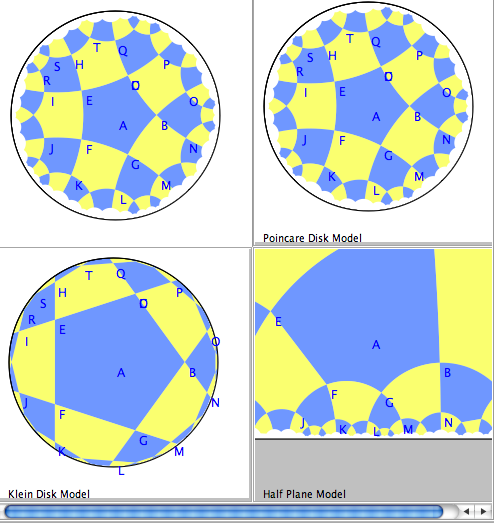 pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions using this week-day code as it is marked "due"
in the syllabus, not by the date you prepare the document.
pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions using this week-day code as it is marked "due"
in the syllabus, not by the date you prepare the document.
\begin{itemize} \item W1: Introduction to the course. A light-weight video transcript of this lecture may be helpful if you missed this lecture. Here is a more readable version of Welcome to 402, but it may take longer start up this mp4.
\item F1: Lesson A1: Greek Geometry from Thales to Pappus with associated Filecard due by noon, W2. Here is a 5min video transcript and a 15min, more detailed video transcript, Lesson A1, follows.
\item M2: Lesson A2: Exterior Angle Lab with an introduction to GeoGebra (GGB) with filecard due before class M2. (The Lab Report is due in 3 weeks.) Here is video for the Absolute Exterior Angle Theome (AXT) in the Euclidean plane. A older lesson on this subject uses the XAT with Geometry Explorer uses a different geometrical construction program.
\item W2: Homework for W2: Browse Advice for Completing this Course. Mark this link to consult throughout the course. Filecard A1 is also due by noon. \item W2 Lesson A3: Axiomatic Systems in Geometry
\item F2 Review of Logic and Mathematical Methods of Proof from MA347.
\item M3 Lesson E1 on Absolute Geometry with filecard.
\item W3 Lesson E2 on Euclid's Parallel Postulate with filecard.
\item F3 Problem Set Due from M4 on. Whatever you hand in on M4 during class time will be corrected and returned before the quiz on F4. Submit both on the Moodle and on a paper printout. Be sure your name and date and solutions submitted are on the first page. You may submit further work until M5, when the entire assignment is due. \item F3 GeoGebra Lab on absolute, Euclidean and hyperbolic exterior angle theorems . The foregoing link is to a video on the lesson. A second video demonstrates that hyperbolic parallels where AIA fails for all, or all but one, transveral.
\item M4 Lesson E3 on John Playfair's Axiom and its equivalent axioms with filecard.
\item W4 Lesson E4 on the Pythagorean Theorem as Euclid proved it. Has filecard.
\item F4 Test on material covered W1-F3. Lessons on M4 and W4 will be on the midterm.
\item M5 Analytic Geometry, Summary and Preview .
\item M5 and W5 Birkhoff's Axioms for Euclidean geometry, for which Cartesian Geometry is an algebraic model.
\item W5 Similarity and the simSAS Axiom .
\item F5 GeoGebra Lab on the hyperbolic model of non-Euclidean geometry. In preparation for this lab, please study these videos, and practice a bit with GeoGebra so we can finish the lab in one session.
Introduction to Inversive Geometry
The Hyperbolic Exterior Angle Theorem
AIA Fails in non-Euclidean Geometry
\item M6. We continue unfinished work from F5, the lab and the discussion of the returned tests. Submit the homework due on M6 as described in the F5 GeoGebra Lab
\item W6. No class.
\item M7. Complex Number Plane begun.
\item W7. Complex Number Plane completed. Filecard due by noon M8.
\item F7 Midterm (6mar15) on the entir semester up to material covered on M6, including how Geogebra is useful for studying both Euclidean and non-Euclidean Geomtry.
\item M8. Special lesson on Filecards and their role in the course and in your grade. Here is the folder M8texPad.zip of files we used today. Be sure you have a copy of texpad.zip to practice and compose your LaTeX filecard answers, as discussed today. For additional information concerning Filecards, see Advice.
\item W8. Moebius Transformations . Filecard due by R8 morning. See also Moebius links . Check for corrections in time for final submission of filecard questions F8.
\item F8. Lab on Moebius Transformations . Last Drop (13mar15).
\item M9. Crossratios and Tripod Theorems . Filecard Z3 Answers are due at noon F9.
\item W9. e Crossratios completed. Preview of the next part of the course.
\item F9. Open Q/A session. Attendance is optional.
\item M10. The Hyperbolic Group . Filecard H1 Answers are due at noon W10.
\item W10. Hyperbolic Distance . Filecard H2 Answers are due at noon M11.
\item F10. Lab on Hyperbolic Translations . With Filecard H3 Answers are due at noon W11.
\item M11. Lesson on Symmety Properties of MTs.
\item W11. Continued, and review on demand.
\item F11. Continued, and review on demand.
\item M12 Hourly Test on Lessons Z1,Z2,Z3,H1,H2,H3 (through F10). \item W12 UHP and Beltrami-Klein models of Non-Euclidean geometry. \item F12 Discussion of Hourly. Beltrami-Klein continued.
\item M13. Lesson on Gauss's Area Theorem (Part 1) \item W13. Lesson on Gauss's Area Theorem (Part 2) \item F13. Lab on Beltrami-Klein Constructions
\item M14. Miscellaneous Review Exercises
\begin{document} Jump to Part II \maketitle
Syllabus "Post-Euclidian Geometry"
MA402 Spring 2015
Instructions
This file is frequently updated. Check the date and reload your browser pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions using this week-day code as it is marked "due"
in the syllabus, not by the date you prepare the document.
pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions using this week-day code as it is marked "due"
in the syllabus, not by the date you prepare the document.
The following syllabus was for last year, Spring 2014. It is here for your information. Some scheduled dates and choice of lessons will differ in the syllabus for Spring 2015. Update your browser frequently. Below is the evolving syllabus for this spring course.
Part I of the Course
Geometry and the Axiomatic Method\begin{itemize} \item W1: Introduction to the course. A light-weight video transcript of this lecture may be helpful if you missed this lecture. Here is a more readable version of Welcome to 402, but it may take longer start up this mp4.
\item F1: Lesson A1: Greek Geometry from Thales to Pappus with associated Filecard due by noon, W2. Here is a 5min video transcript and a 15min, more detailed video transcript, Lesson A1, follows.
\item M2: Lesson A2: Exterior Angle Lab with an introduction to GeoGebra (GGB) with filecard due before class M2. (The Lab Report is due in 3 weeks.) Here is video for the Absolute Exterior Angle Theome (AXT) in the Euclidean plane. A older lesson on this subject uses the XAT with Geometry Explorer uses a different geometrical construction program.
\item W2: Homework for W2: Browse Advice for Completing this Course. Mark this link to consult throughout the course. Filecard A1 is also due by noon. \item W2 Lesson A3: Axiomatic Systems in Geometry
\item F2 Review of Logic and Mathematical Methods of Proof from MA347.
\item M3 Lesson E1 on Absolute Geometry with filecard.
\item W3 Lesson E2 on Euclid's Parallel Postulate with filecard.
\item F3 Problem Set Due from M4 on. Whatever you hand in on M4 during class time will be corrected and returned before the quiz on F4. Submit both on the Moodle and on a paper printout. Be sure your name and date and solutions submitted are on the first page. You may submit further work until M5, when the entire assignment is due. \item F3 GeoGebra Lab on absolute, Euclidean and hyperbolic exterior angle theorems . The foregoing link is to a video on the lesson. A second video demonstrates that hyperbolic parallels where AIA fails for all, or all but one, transveral.
\item M4 Lesson E3 on John Playfair's Axiom and its equivalent axioms with filecard.
\item W4 Lesson E4 on the Pythagorean Theorem as Euclid proved it. Has filecard.
\item F4 Test on material covered W1-F3. Lessons on M4 and W4 will be on the midterm.
\item M5 Analytic Geometry, Summary and Preview .
\item M5 and W5 Birkhoff's Axioms for Euclidean geometry, for which Cartesian Geometry is an algebraic model.
\item W5 Similarity and the simSAS Axiom .
\item F5 GeoGebra Lab on the hyperbolic model of non-Euclidean geometry. In preparation for this lab, please study these videos, and practice a bit with GeoGebra so we can finish the lab in one session.
Introduction to Inversive Geometry
The Hyperbolic Exterior Angle Theorem
AIA Fails in non-Euclidean Geometry
\item M6. We continue unfinished work from F5, the lab and the discussion of the returned tests. Submit the homework due on M6 as described in the F5 GeoGebra Lab
\item W6. No class.
Part II of the Course
\item F6. Introduction to Complex Numbers and GeoGebra Lab.\item M7. Complex Number Plane begun.
\item W7. Complex Number Plane completed. Filecard due by noon M8.
\item F7 Midterm (6mar15) on the entir semester up to material covered on M6, including how Geogebra is useful for studying both Euclidean and non-Euclidean Geomtry.
\item M8. Special lesson on Filecards and their role in the course and in your grade. Here is the folder M8texPad.zip of files we used today. Be sure you have a copy of texpad.zip to practice and compose your LaTeX filecard answers, as discussed today. For additional information concerning Filecards, see Advice.
\item W8. Moebius Transformations . Filecard due by R8 morning. See also Moebius links . Check for corrections in time for final submission of filecard questions F8.
\item F8. Lab on Moebius Transformations . Last Drop (13mar15).
\item M9. Crossratios and Tripod Theorems . Filecard Z3 Answers are due at noon F9.
\item W9. e Crossratios completed. Preview of the next part of the course.
\item F9. Open Q/A session. Attendance is optional.
\item M10. The Hyperbolic Group . Filecard H1 Answers are due at noon W10.
\item W10. Hyperbolic Distance . Filecard H2 Answers are due at noon M11.
\item F10. Lab on Hyperbolic Translations . With Filecard H3 Answers are due at noon W11.
\item M11. Lesson on Symmety Properties of MTs.
\item W11. Continued, and review on demand.
\item F11. Continued, and review on demand.
\item M12 Hourly Test on Lessons Z1,Z2,Z3,H1,H2,H3 (through F10). \item W12 UHP and Beltrami-Klein models of Non-Euclidean geometry. \item F12 Discussion of Hourly. Beltrami-Klein continued.
\item M13. Lesson on Gauss's Area Theorem (Part 1) \item W13. Lesson on Gauss's Area Theorem (Part 2) \item F13. Lab on Beltrami-Klein Constructions
\item M14. Miscellaneous Review Exercises
Last edited 15mar15
\begin{document} Jump to Part II \maketitleSyllabus "Post-Euclidian Geometry"
MA402 Spring 2015
Instructions
This file is frequently updated. Check the date and reload your browserpages each time you visit. Note the convention that "F1" means "Friday of Week 1". Label all course submissions using this week-day code as it is marked "due" in the syllabus, not by the date you prepare the document.
The following syllabus was for last year, Spring 2014. It is here for your information. Some scheduled dates and choice of lessons will differ in the syllabus for Spring 2015. Update your browser frequently. Below is the evolving syllabus for this spring course.
Part I of the Course
Geometry and the Axiomatic Method
\begin{itemize} \item W1: Introduction to the course. A light-weight video transcript of this lecture may be helpful if you missed this lecture. Here is a more readable version of Welcome to 402, but it may take longer start up this mp4.
\item F1: Lesson A1: Greek Geometry from Thales to Pappus with associated Filecard due by noon, W2. Here is a 5min video transcript and a 15min, more detailed video transcript, Lesson A1, follows.
\item M2: Lesson A2: Exterior Angle Lab with an introduction to GeoGebra (GGB) with filecard due before class M2. (The Lab Report is due in 3 weeks.) Here is video for the Absolute Exterior Angle Theome (AXT) in the Euclidean plane. A older lesson on this subject uses the XAT with Geometry Explorer uses a different geometrical construction program.
\item W2: Homework for W2: Browse Advice for Completing this Course. Mark this link to consult throughout the course. Filecard A1 is also due by noon. \item W2 Lesson A3: Axiomatic Systems in Geometry
\item F2 Review of Logic and Mathematical Methods of Proof from MA347.
\item M3 Lesson E1 on Absolute Geometry with filecard.
\item W3 Lesson E2 on Euclid's Parallel Postulate with filecard.
\item F3 Problem Set Due from M4 on. Whatever you hand in on M4 during class time will be corrected and returned before the quiz on F4. Submit both on the Moodle and on a paper printout. Be sure your name and date and solutions submitted are on the first page. You may submit further work until M5, when the entire assignment is due. \item F3 GeoGebra Lab on absolute, Euclidean and hyperbolic exterior angle theorems . The foregoing link is to a video on the lesson. A second video demonstrates that hyperbolic parallels where AIA fails for all, or all but one, transveral.
\item M4 Lesson E3 on John Playfair's Axiom and its equivalent axioms with filecard.
\item W4 Lesson E4 on the Pythagorean Theorem as Euclid proved it. Has filecard.
\item F4 Test on material covered W1-F3. Lessons on M4 and W4 will be on the midterm.
\item M5 Analytic Geometry, Summary and Preview .
\item M5 and W5 Birkhoff's Axioms for Euclidean geometry, for which Cartesian Geometry is an algebraic model.
\item W5 Similarity and the simSAS Axiom .
\item F5 GeoGebra Lab on the hyperbolic model of non-Euclidean geometry. In preparation for this lab, please study these videos, and practice a bit with GeoGebra so we can finish the lab in one session.
Introduction to Inversive Geometry
The Hyperbolic Exterior Angle Theorem
AIA Fails in non-Euclidean Geometry
\item M6. We continue unfinished work from F5, the lab and the discussion of the returned tests. Submit the homework due on M6 as described in the F5 GeoGebra Lab
\item W6. No class.Part II of the Course
\item F6. Introduction to Complex Numbers and GeoGebra Lab.
\item M7. Complex Number Plane begun.
\item W7. Complex Number Plane completed. Filecard due by noon M8.
\item F7 Midterm (6mar15) on the entir semester up to material covered on M6, including how Geogebra is useful for studying both Euclidean and non-Euclidean Geomtry.
\item M8. Special lesson on Filecards and their role in the course and in your grade. Here is the folder M8texPad.zip of files we used today. Be sure you have a copy of texpad.zip to practice and compose your LaTeX filecard answers, as discussed today. For additional information concerning Filecards, see Advice.
\item W8. Moebius Transformations . Filecard due by R8 morning. See also Moebius links . Check for corrections in time for final submission of filecard questions F8.
\item F8. Lab on Moebius Transformations . Last Drop (13mar15).
\item M9. Crossratios and Tripod Theorems . Filecard Z3 Answers are due at noon F9.
\item W9. e Crossratios completed. Preview of the next part of the course.
\item F9. Open Q/A session. Attendance is optional.
\item M10. The Hyperbolic Group . Filecard H1 Answers are due at noon W10.
\item W10. Hyperbolic Distance . Filecard H2 Answers are due at noon M11.
\item F10. Lab on Hyperbolic Translations . With Filecard H3 Answers are due at noon W11.
\item M11. Lesson on Symmety Properties of MTs.
\item W11. Continued, and review on demand.
\item F11. Continued, and review on demand.
\item M12 Hourly Test on Lessons Z1,Z2,Z3,H1,H2,H3 (through F10). \item W12 UHP and Beltrami-Klein models of Non-Euclidean geometry. \item F12 Discussion of Hourly. Beltrami-Klein continued.
\item M13. Lesson on Gauss's Area Theorem (Part 1) \item W13. Lesson on Gauss's Area Theorem (Part 2) \item F13. Lab on Beltrami-Klein Constructions
TEMPORARY END OF FILE
======================================================================== ======================================================================= =================================================================== =============================================================== =========================================================== \end{document}