Last updated 7may11.
\begin{document} \section{Introduction} Thanks to the ubiquity of Google and other search engines, an enormous
source of information is at your finger tips at almost all of the time.
Much of it is overwhelming, and some of it is wrong. But
mostly, the result of undigested googling leads to misplaced emphases
and mental indigestion.
So here you will find comments on the text and lessons,
which you can always expand more fully
by googling the web. Think of this material as study guides.
This lesson supplements Hvidsten 1.2 and should be completed in the
first week of the course.
When you have understood a section, write about it in your Journal (see
Advice).
\section{Origins of Greek Geometry}
Let start by setting up an easily remembered (if approximate) timeline.
This gives you the framework where the geometry of the Greeks fits
in human history. Geometry was discovered and developed elsewhere as
well. But not being a history course, we'll stick to Euclid's world
and patrimony here.
\begin{itemize}
\item[-900] Egypt, Mesopotamia, Persia, surveying and astronomy
\item[-600] Greece: Thales, Pythagoras
\item[-300] Euclid, Eudoxus
\item[-200] Archimedes, Apollonius
\item[+300] Pappus of Alexandria
\item[+800] Baghdad: algebra, preserving of Euclidean geometry
\item[+1000] Europe: universities
\item[+1600] Newton, Leibniz, calculus
\item[+1800] Gauss, Lobachevsky, Bolyai, non-Euclidean geometry
\item[+1850] Riemann, Poincare, Klein, modern geometry
\item[+1900] Hilbert, end of the Parallel Postulate Problem.
\end{itemize}
\section{Thales' Theorems}
It is said that Thales knew proofs of five important theorems. His works are
lost, so we don't really know whether his proofs were correct. The five
theorems can be easily remembered by mnemonic figures.
Thanks to the ubiquity of Google and other search engines, an enormous
source of information is at your finger tips at almost all of the time.
Much of it is overwhelming, and some of it is wrong. But
mostly, the result of undigested googling leads to misplaced emphases
and mental indigestion.
So here you will find comments on the text and lessons,
which you can always expand more fully
by googling the web. Think of this material as study guides.
This lesson supplements Hvidsten 1.2 and should be completed in the
first week of the course.
When you have understood a section, write about it in your Journal (see
Advice).
\section{Origins of Greek Geometry}
Let start by setting up an easily remembered (if approximate) timeline.
This gives you the framework where the geometry of the Greeks fits
in human history. Geometry was discovered and developed elsewhere as
well. But not being a history course, we'll stick to Euclid's world
and patrimony here.
\begin{itemize}
\item[-900] Egypt, Mesopotamia, Persia, surveying and astronomy
\item[-600] Greece: Thales, Pythagoras
\item[-300] Euclid, Eudoxus
\item[-200] Archimedes, Apollonius
\item[+300] Pappus of Alexandria
\item[+800] Baghdad: algebra, preserving of Euclidean geometry
\item[+1000] Europe: universities
\item[+1600] Newton, Leibniz, calculus
\item[+1800] Gauss, Lobachevsky, Bolyai, non-Euclidean geometry
\item[+1850] Riemann, Poincare, Klein, modern geometry
\item[+1900] Hilbert, end of the Parallel Postulate Problem.
\end{itemize}
\section{Thales' Theorems}
It is said that Thales knew proofs of five important theorems. His works are
lost, so we don't really know whether his proofs were correct. The five
theorems can be easily remembered by mnemonic figures.
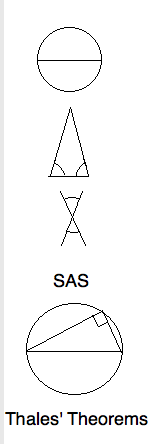 \begin{itemize}
\itemT1. That the diameter bisects the circle seems too obvious to prove.
Perhaps Thales meant something more profound by the word ``bisects".
\itemT2. A triangle is \textit{isosceles} if two of its sides are equal.
That this implies equal base angle isn't as obvious as 1. In fact, Euclid
felt obliged to prove this in a very complicated way.
\itemT3. Like the first two theorem, that vertical angles are equal is
another observation that can be deduced from symmetry. Not so the next two.
\itemT4. The Side-Angle-Side criterion for two triangles to be congruent
is a profound observation. Euclid's proof is incomplete. Indeed, Hilbert
takes this as an axiom, not because it is obvious, but because it is a
powerful place to start.
\itemT5. That all triangles inscribed in a semicircle are right triangles
is generally just called \textit{Thales' Theorem.}
\end{itemize}
\section{Pappus' Proof of Pons Asinorum}
Thales' second theorem generally known by its medieval name,
\textit{pons asinorum} (bridge of asses), because stupid, or
stubborn geometry students could not master its proof.
In the early days of computers, MIT scientists programmed one
to discover and prove simple geometrical theorems. Most of the
theorems it discovered were uninteresting, as were its
deduction from the axioms and previous theorems it had discovered.
But when the computer ``rediscovered" Pappus' argument using SAS
the artificial intelligence community was mightly pleased. The
proof in the classical two column format might look like this:
\begin{itemize}
\itemT1. That the diameter bisects the circle seems too obvious to prove.
Perhaps Thales meant something more profound by the word ``bisects".
\itemT2. A triangle is \textit{isosceles} if two of its sides are equal.
That this implies equal base angle isn't as obvious as 1. In fact, Euclid
felt obliged to prove this in a very complicated way.
\itemT3. Like the first two theorem, that vertical angles are equal is
another observation that can be deduced from symmetry. Not so the next two.
\itemT4. The Side-Angle-Side criterion for two triangles to be congruent
is a profound observation. Euclid's proof is incomplete. Indeed, Hilbert
takes this as an axiom, not because it is obvious, but because it is a
powerful place to start.
\itemT5. That all triangles inscribed in a semicircle are right triangles
is generally just called \textit{Thales' Theorem.}
\end{itemize}
\section{Pappus' Proof of Pons Asinorum}
Thales' second theorem generally known by its medieval name,
\textit{pons asinorum} (bridge of asses), because stupid, or
stubborn geometry students could not master its proof.
In the early days of computers, MIT scientists programmed one
to discover and prove simple geometrical theorems. Most of the
theorems it discovered were uninteresting, as were its
deduction from the axioms and previous theorems it had discovered.
But when the computer ``rediscovered" Pappus' argument using SAS
the artificial intelligence community was mightly pleased. The
proof in the classical two column format might look like this:
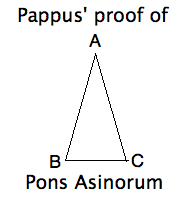 \begin{eqnarray*}
AB & \cong & AC & \mbox{given isosceles} \\
\angle BAC & \cong& \angle CAB & \mbox{same angle} \\
AC& \cong& AB & \mbox{given isosceles} \\
\therefore \triangle BAC & \cong& \triangle CAB & \mbox{by SAS} \\
\therefore \angle ABC& \cong& \angle ACB & \mbox{by congruence} \\
\end{eqnarray*}
\section{Hvidsten's Proof of Thales' Theorem}
In Sec. 1.2.2, the author invites the reader with a ``Try proving this theorem".
Such invitations are common in math books.
Coming this early in the text
suggests that somehow not being able to supply the proof, a
student is unprepared for the course.
We'll interpret this as an
invitation to the teacher to elaborate, and derive some extra
mileage. However, such ``internal exercises" should never be ignored.
They give the reader insight into the author's level of discourse.
Ignoring them leads to the common complaint by students that the
exposition is ``confusing". Whenever you are tempted to dismiss an
argument as simply confusing, you should reflect on, and formulate
just what you don't understand, and possibly why.
First, connect the vertex $D$ with the center $B$ of the
circle.
Compare the picture on the right with that in the text. Note that
the angles $\gamma, \beta$ are repeated by \textit{pons asinorum}
(both triangles are isosceles).
\begin{eqnarray*}
AB & \cong & AC & \mbox{given isosceles} \\
\angle BAC & \cong& \angle CAB & \mbox{same angle} \\
AC& \cong& AB & \mbox{given isosceles} \\
\therefore \triangle BAC & \cong& \triangle CAB & \mbox{by SAS} \\
\therefore \angle ABC& \cong& \angle ACB & \mbox{by congruence} \\
\end{eqnarray*}
\section{Hvidsten's Proof of Thales' Theorem}
In Sec. 1.2.2, the author invites the reader with a ``Try proving this theorem".
Such invitations are common in math books.
Coming this early in the text
suggests that somehow not being able to supply the proof, a
student is unprepared for the course.
We'll interpret this as an
invitation to the teacher to elaborate, and derive some extra
mileage. However, such ``internal exercises" should never be ignored.
They give the reader insight into the author's level of discourse.
Ignoring them leads to the common complaint by students that the
exposition is ``confusing". Whenever you are tempted to dismiss an
argument as simply confusing, you should reflect on, and formulate
just what you don't understand, and possibly why.
First, connect the vertex $D$ with the center $B$ of the
circle.
Compare the picture on the right with that in the text. Note that
the angles $\gamma, \beta$ are repeated by \textit{pons asinorum}
(both triangles are isosceles).
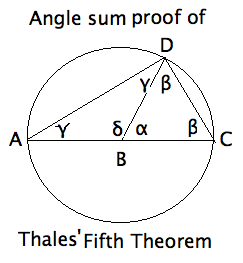 The author suggests using the ``prior" theorem that the angles
of a triangle add up to $pi$. Actually, this \textit{Angle Sum
Theorem} is equivalent to the \textit{Exterior Angle Theorem }
(or EXAT for short). It says that the exterior angle of
a triangle equals the sum of the opposite interior angles.
We shall see a great deal of this theorem. In our figure,
\begin{eqnarray*}
\angle \alpha &=& 2 \angle \gamma \\
\angle \delta &=& 2 \angle \beta \\
\therefore \angle \alpha + \angle \delta &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \pi &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \frac{\pi}{2} &=& \angle ADC \\
\therefore \triangle ADC & = & \mbox { a right triangle } \\
\end{eqnarray*}
\section{Exterior Angle Theorem}
There are two exterior angle theorems in
\textit{Euclid's Elements}. The first just says that the
exterior angle of a triangle is greater than either of the
The author suggests using the ``prior" theorem that the angles
of a triangle add up to $pi$. Actually, this \textit{Angle Sum
Theorem} is equivalent to the \textit{Exterior Angle Theorem }
(or EXAT for short). It says that the exterior angle of
a triangle equals the sum of the opposite interior angles.
We shall see a great deal of this theorem. In our figure,
\begin{eqnarray*}
\angle \alpha &=& 2 \angle \gamma \\
\angle \delta &=& 2 \angle \beta \\
\therefore \angle \alpha + \angle \delta &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \pi &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \frac{\pi}{2} &=& \angle ADC \\
\therefore \triangle ADC & = & \mbox { a right triangle } \\
\end{eqnarray*}
\section{Exterior Angle Theorem}
There are two exterior angle theorems in
\textit{Euclid's Elements}. The first just says that the
exterior angle of a triangle is greater than either of the
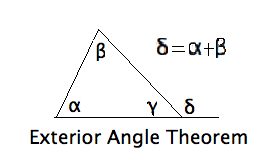 two opposite interior angles, and we'll study a particular proof of
this later in the course. The more precise form used
here is peculiarly Euclidean, and fails in other geometries.
You can now begin reading \textit{The Axiomatic Method}, which summarizes
what we are about to study.
\section{Archimedes' Angle Trisection}
Perhaps you have heard of the impossibility of trisecting an arbitrary angle
by ruler and compass. The ancients suspected it, but the theorem was not proved
until the 19th century, using modern algebraic methods. Cranks still circulate
``solutions", but their efforts contribute nothing to mathematics.
two opposite interior angles, and we'll study a particular proof of
this later in the course. The more precise form used
here is peculiarly Euclidean, and fails in other geometries.
You can now begin reading \textit{The Axiomatic Method}, which summarizes
what we are about to study.
\section{Archimedes' Angle Trisection}
Perhaps you have heard of the impossibility of trisecting an arbitrary angle
by ruler and compass. The ancients suspected it, but the theorem was not proved
until the 19th century, using modern algebraic methods. Cranks still circulate
``solutions", but their efforts contribute nothing to mathematics.
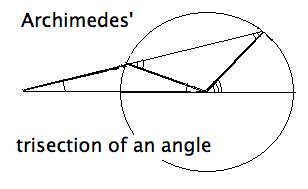 The Greeks did know that if additional tools were allowed, for example certain
curves, then trisections became possible. Recall that their rulers were considered
unmarked \textit{straight-edges}. Archimedes, the greatest mathematician and
physicist of the ancient world, showed that if you were allowed to make two
marks on a ruler, it is possible. And all it takes is the EXAT.
In the figure, the given angle is on the right. I have omitted letter labels to
wean you away from such geometric training wheels. Letter labels make it too easy just to check each
item stated. The real world comes without labels, and you should learn to
``read" a figure without them. So, draw a circle about the given angle, and
extend one side of the angle to an entire diameter, and then extend this
diameters as far to the left as needed. Euclids second postulate says that
you can do this. Modern geometry considers all lines to be infinite anyway.
Now mark a segment on a straight-edge equal to the radius of the circle.
Place the marked ruler in such a way that it passes through the end of
the other side of the angle, crosses the circle and lands on the extended
diamater exactly one radius distance further on. In the figure three segments
the length of a radius are marked more heavily. They form the sides of
two isosceles triangles. By \textit{Pons Asinorum} and EXAT applied
two times, the smallest angle is one-third the size of the original angle.
The angle marks help see the relationships.
\section{Symbolic Logic}
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
the sentence I used above:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``ifs" and
``thens". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{propositions} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". If we rewrite ``D = A => (B=>C)", you should now prove that
D and E are equivalent by the rules of the symbolic logic. Do it!
\section{Filecard}
Please fill out this
Filecard A1 on this lesson.
\section{LaTeX, HTML and Ascii Notation}
In this course we'll use a variety of mathematical notation, all of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
Here we list the notation needed to make this document typographically correct.
As of 9jan12, using augmented ltmml.js, the LaTeX term on the left prints like
the symbol on the right. But only Firefox browsers can interpret a web language called \it{MathML} correctly. For Internet Explorer through IE8, there is a
plugin on the web for this purpose which no longer works for IE9.
Other browsers, like Chrome and Safari, will not do this reliably. In LaTeX
(as in texWins) the code on the left also prints the symbol on the right,
and does the curly phi correctly. If you're curious as to why, you can
follows this silly debate among experts on the web. Consult the Advice
pages for more information.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}
The Greeks did know that if additional tools were allowed, for example certain
curves, then trisections became possible. Recall that their rulers were considered
unmarked \textit{straight-edges}. Archimedes, the greatest mathematician and
physicist of the ancient world, showed that if you were allowed to make two
marks on a ruler, it is possible. And all it takes is the EXAT.
In the figure, the given angle is on the right. I have omitted letter labels to
wean you away from such geometric training wheels. Letter labels make it too easy just to check each
item stated. The real world comes without labels, and you should learn to
``read" a figure without them. So, draw a circle about the given angle, and
extend one side of the angle to an entire diameter, and then extend this
diameters as far to the left as needed. Euclids second postulate says that
you can do this. Modern geometry considers all lines to be infinite anyway.
Now mark a segment on a straight-edge equal to the radius of the circle.
Place the marked ruler in such a way that it passes through the end of
the other side of the angle, crosses the circle and lands on the extended
diamater exactly one radius distance further on. In the figure three segments
the length of a radius are marked more heavily. They form the sides of
two isosceles triangles. By \textit{Pons Asinorum} and EXAT applied
two times, the smallest angle is one-third the size of the original angle.
The angle marks help see the relationships.
\section{Symbolic Logic}
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
the sentence I used above:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``ifs" and
``thens". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{propositions} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". If we rewrite ``D = A => (B=>C)", you should now prove that
D and E are equivalent by the rules of the symbolic logic. Do it!
\section{Filecard}
Please fill out this
Filecard A1 on this lesson.
\section{LaTeX, HTML and Ascii Notation}
In this course we'll use a variety of mathematical notation, all of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
Here we list the notation needed to make this document typographically correct.
As of 9jan12, using augmented ltmml.js, the LaTeX term on the left prints like
the symbol on the right. But only Firefox browsers can interpret a web language called \it{MathML} correctly. For Internet Explorer through IE8, there is a
plugin on the web for this purpose which no longer works for IE9.
Other browsers, like Chrome and Safari, will not do this reliably. In LaTeX
(as in texWins) the code on the left also prints the symbol on the right,
and does the curly phi correctly. If you're curious as to why, you can
follows this silly debate among experts on the web. Consult the Advice
pages for more information.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}
Greek Geometry: Thales to Pappus
\textit{ $\C$ 2010, Prof. George K. Francis, Mathematics Department, University of Illinois}\begin{document} \section{Introduction}
 Thanks to the ubiquity of Google and other search engines, an enormous
source of information is at your finger tips at almost all of the time.
Much of it is overwhelming, and some of it is wrong. But
mostly, the result of undigested googling leads to misplaced emphases
and mental indigestion.
So here you will find comments on the text and lessons,
which you can always expand more fully
by googling the web. Think of this material as study guides.
This lesson supplements Hvidsten 1.2 and should be completed in the
first week of the course.
When you have understood a section, write about it in your Journal (see
Advice).
\section{Origins of Greek Geometry}
Let start by setting up an easily remembered (if approximate) timeline.
This gives you the framework where the geometry of the Greeks fits
in human history. Geometry was discovered and developed elsewhere as
well. But not being a history course, we'll stick to Euclid's world
and patrimony here.
\begin{itemize}
\item[-900] Egypt, Mesopotamia, Persia, surveying and astronomy
\item[-600] Greece: Thales, Pythagoras
\item[-300] Euclid, Eudoxus
\item[-200] Archimedes, Apollonius
\item[+300] Pappus of Alexandria
\item[+800] Baghdad: algebra, preserving of Euclidean geometry
\item[+1000] Europe: universities
\item[+1600] Newton, Leibniz, calculus
\item[+1800] Gauss, Lobachevsky, Bolyai, non-Euclidean geometry
\item[+1850] Riemann, Poincare, Klein, modern geometry
\item[+1900] Hilbert, end of the Parallel Postulate Problem.
\end{itemize}
\section{Thales' Theorems}
It is said that Thales knew proofs of five important theorems. His works are
lost, so we don't really know whether his proofs were correct. The five
theorems can be easily remembered by mnemonic figures.
Thanks to the ubiquity of Google and other search engines, an enormous
source of information is at your finger tips at almost all of the time.
Much of it is overwhelming, and some of it is wrong. But
mostly, the result of undigested googling leads to misplaced emphases
and mental indigestion.
So here you will find comments on the text and lessons,
which you can always expand more fully
by googling the web. Think of this material as study guides.
This lesson supplements Hvidsten 1.2 and should be completed in the
first week of the course.
When you have understood a section, write about it in your Journal (see
Advice).
\section{Origins of Greek Geometry}
Let start by setting up an easily remembered (if approximate) timeline.
This gives you the framework where the geometry of the Greeks fits
in human history. Geometry was discovered and developed elsewhere as
well. But not being a history course, we'll stick to Euclid's world
and patrimony here.
\begin{itemize}
\item[-900] Egypt, Mesopotamia, Persia, surveying and astronomy
\item[-600] Greece: Thales, Pythagoras
\item[-300] Euclid, Eudoxus
\item[-200] Archimedes, Apollonius
\item[+300] Pappus of Alexandria
\item[+800] Baghdad: algebra, preserving of Euclidean geometry
\item[+1000] Europe: universities
\item[+1600] Newton, Leibniz, calculus
\item[+1800] Gauss, Lobachevsky, Bolyai, non-Euclidean geometry
\item[+1850] Riemann, Poincare, Klein, modern geometry
\item[+1900] Hilbert, end of the Parallel Postulate Problem.
\end{itemize}
\section{Thales' Theorems}
It is said that Thales knew proofs of five important theorems. His works are
lost, so we don't really know whether his proofs were correct. The five
theorems can be easily remembered by mnemonic figures.
 \begin{itemize}
\itemT1. That the diameter bisects the circle seems too obvious to prove.
Perhaps Thales meant something more profound by the word ``bisects".
\itemT2. A triangle is \textit{isosceles} if two of its sides are equal.
That this implies equal base angle isn't as obvious as 1. In fact, Euclid
felt obliged to prove this in a very complicated way.
\itemT3. Like the first two theorem, that vertical angles are equal is
another observation that can be deduced from symmetry. Not so the next two.
\itemT4. The Side-Angle-Side criterion for two triangles to be congruent
is a profound observation. Euclid's proof is incomplete. Indeed, Hilbert
takes this as an axiom, not because it is obvious, but because it is a
powerful place to start.
\itemT5. That all triangles inscribed in a semicircle are right triangles
is generally just called \textit{Thales' Theorem.}
\end{itemize}
\section{Pappus' Proof of Pons Asinorum}
Thales' second theorem generally known by its medieval name,
\textit{pons asinorum} (bridge of asses), because stupid, or
stubborn geometry students could not master its proof.
In the early days of computers, MIT scientists programmed one
to discover and prove simple geometrical theorems. Most of the
theorems it discovered were uninteresting, as were its
deduction from the axioms and previous theorems it had discovered.
But when the computer ``rediscovered" Pappus' argument using SAS
the artificial intelligence community was mightly pleased. The
proof in the classical two column format might look like this:
\begin{itemize}
\itemT1. That the diameter bisects the circle seems too obvious to prove.
Perhaps Thales meant something more profound by the word ``bisects".
\itemT2. A triangle is \textit{isosceles} if two of its sides are equal.
That this implies equal base angle isn't as obvious as 1. In fact, Euclid
felt obliged to prove this in a very complicated way.
\itemT3. Like the first two theorem, that vertical angles are equal is
another observation that can be deduced from symmetry. Not so the next two.
\itemT4. The Side-Angle-Side criterion for two triangles to be congruent
is a profound observation. Euclid's proof is incomplete. Indeed, Hilbert
takes this as an axiom, not because it is obvious, but because it is a
powerful place to start.
\itemT5. That all triangles inscribed in a semicircle are right triangles
is generally just called \textit{Thales' Theorem.}
\end{itemize}
\section{Pappus' Proof of Pons Asinorum}
Thales' second theorem generally known by its medieval name,
\textit{pons asinorum} (bridge of asses), because stupid, or
stubborn geometry students could not master its proof.
In the early days of computers, MIT scientists programmed one
to discover and prove simple geometrical theorems. Most of the
theorems it discovered were uninteresting, as were its
deduction from the axioms and previous theorems it had discovered.
But when the computer ``rediscovered" Pappus' argument using SAS
the artificial intelligence community was mightly pleased. The
proof in the classical two column format might look like this:
 \begin{eqnarray*}
AB & \cong & AC & \mbox{given isosceles} \\
\angle BAC & \cong& \angle CAB & \mbox{same angle} \\
AC& \cong& AB & \mbox{given isosceles} \\
\therefore \triangle BAC & \cong& \triangle CAB & \mbox{by SAS} \\
\therefore \angle ABC& \cong& \angle ACB & \mbox{by congruence} \\
\end{eqnarray*}
\section{Hvidsten's Proof of Thales' Theorem}
In Sec. 1.2.2, the author invites the reader with a ``Try proving this theorem".
Such invitations are common in math books.
Coming this early in the text
suggests that somehow not being able to supply the proof, a
student is unprepared for the course.
We'll interpret this as an
invitation to the teacher to elaborate, and derive some extra
mileage. However, such ``internal exercises" should never be ignored.
They give the reader insight into the author's level of discourse.
Ignoring them leads to the common complaint by students that the
exposition is ``confusing". Whenever you are tempted to dismiss an
argument as simply confusing, you should reflect on, and formulate
just what you don't understand, and possibly why.
First, connect the vertex $D$ with the center $B$ of the
circle.
Compare the picture on the right with that in the text. Note that
the angles $\gamma, \beta$ are repeated by \textit{pons asinorum}
(both triangles are isosceles).
\begin{eqnarray*}
AB & \cong & AC & \mbox{given isosceles} \\
\angle BAC & \cong& \angle CAB & \mbox{same angle} \\
AC& \cong& AB & \mbox{given isosceles} \\
\therefore \triangle BAC & \cong& \triangle CAB & \mbox{by SAS} \\
\therefore \angle ABC& \cong& \angle ACB & \mbox{by congruence} \\
\end{eqnarray*}
\section{Hvidsten's Proof of Thales' Theorem}
In Sec. 1.2.2, the author invites the reader with a ``Try proving this theorem".
Such invitations are common in math books.
Coming this early in the text
suggests that somehow not being able to supply the proof, a
student is unprepared for the course.
We'll interpret this as an
invitation to the teacher to elaborate, and derive some extra
mileage. However, such ``internal exercises" should never be ignored.
They give the reader insight into the author's level of discourse.
Ignoring them leads to the common complaint by students that the
exposition is ``confusing". Whenever you are tempted to dismiss an
argument as simply confusing, you should reflect on, and formulate
just what you don't understand, and possibly why.
First, connect the vertex $D$ with the center $B$ of the
circle.
Compare the picture on the right with that in the text. Note that
the angles $\gamma, \beta$ are repeated by \textit{pons asinorum}
(both triangles are isosceles).
 The author suggests using the ``prior" theorem that the angles
of a triangle add up to $pi$. Actually, this \textit{Angle Sum
Theorem} is equivalent to the \textit{Exterior Angle Theorem }
(or EXAT for short). It says that the exterior angle of
a triangle equals the sum of the opposite interior angles.
We shall see a great deal of this theorem. In our figure,
\begin{eqnarray*}
\angle \alpha &=& 2 \angle \gamma \\
\angle \delta &=& 2 \angle \beta \\
\therefore \angle \alpha + \angle \delta &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \pi &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \frac{\pi}{2} &=& \angle ADC \\
\therefore \triangle ADC & = & \mbox { a right triangle } \\
\end{eqnarray*}
\section{Exterior Angle Theorem}
There are two exterior angle theorems in
\textit{Euclid's Elements}. The first just says that the
exterior angle of a triangle is greater than either of the
The author suggests using the ``prior" theorem that the angles
of a triangle add up to $pi$. Actually, this \textit{Angle Sum
Theorem} is equivalent to the \textit{Exterior Angle Theorem }
(or EXAT for short). It says that the exterior angle of
a triangle equals the sum of the opposite interior angles.
We shall see a great deal of this theorem. In our figure,
\begin{eqnarray*}
\angle \alpha &=& 2 \angle \gamma \\
\angle \delta &=& 2 \angle \beta \\
\therefore \angle \alpha + \angle \delta &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \pi &=& 2 (\angle \gamma + \angle \beta) \\
\therefore \frac{\pi}{2} &=& \angle ADC \\
\therefore \triangle ADC & = & \mbox { a right triangle } \\
\end{eqnarray*}
\section{Exterior Angle Theorem}
There are two exterior angle theorems in
\textit{Euclid's Elements}. The first just says that the
exterior angle of a triangle is greater than either of the
 two opposite interior angles, and we'll study a particular proof of
this later in the course. The more precise form used
here is peculiarly Euclidean, and fails in other geometries.
You can now begin reading \textit{The Axiomatic Method}, which summarizes
what we are about to study.
\section{Archimedes' Angle Trisection}
Perhaps you have heard of the impossibility of trisecting an arbitrary angle
by ruler and compass. The ancients suspected it, but the theorem was not proved
until the 19th century, using modern algebraic methods. Cranks still circulate
``solutions", but their efforts contribute nothing to mathematics.
two opposite interior angles, and we'll study a particular proof of
this later in the course. The more precise form used
here is peculiarly Euclidean, and fails in other geometries.
You can now begin reading \textit{The Axiomatic Method}, which summarizes
what we are about to study.
\section{Archimedes' Angle Trisection}
Perhaps you have heard of the impossibility of trisecting an arbitrary angle
by ruler and compass. The ancients suspected it, but the theorem was not proved
until the 19th century, using modern algebraic methods. Cranks still circulate
``solutions", but their efforts contribute nothing to mathematics.
 The Greeks did know that if additional tools were allowed, for example certain
curves, then trisections became possible. Recall that their rulers were considered
unmarked \textit{straight-edges}. Archimedes, the greatest mathematician and
physicist of the ancient world, showed that if you were allowed to make two
marks on a ruler, it is possible. And all it takes is the EXAT.
In the figure, the given angle is on the right. I have omitted letter labels to
wean you away from such geometric training wheels. Letter labels make it too easy just to check each
item stated. The real world comes without labels, and you should learn to
``read" a figure without them. So, draw a circle about the given angle, and
extend one side of the angle to an entire diameter, and then extend this
diameters as far to the left as needed. Euclids second postulate says that
you can do this. Modern geometry considers all lines to be infinite anyway.
Now mark a segment on a straight-edge equal to the radius of the circle.
Place the marked ruler in such a way that it passes through the end of
the other side of the angle, crosses the circle and lands on the extended
diamater exactly one radius distance further on. In the figure three segments
the length of a radius are marked more heavily. They form the sides of
two isosceles triangles. By \textit{Pons Asinorum} and EXAT applied
two times, the smallest angle is one-third the size of the original angle.
The angle marks help see the relationships.
\section{Symbolic Logic}
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
the sentence I used above:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``ifs" and
``thens". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{propositions} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". If we rewrite ``D = A => (B=>C)", you should now prove that
D and E are equivalent by the rules of the symbolic logic. Do it!
\section{Filecard}
Please fill out this
Filecard A1 on this lesson.
\section{LaTeX, HTML and Ascii Notation}
In this course we'll use a variety of mathematical notation, all of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
Here we list the notation needed to make this document typographically correct.
As of 9jan12, using augmented ltmml.js, the LaTeX term on the left prints like
the symbol on the right. But only Firefox browsers can interpret a web language called \it{MathML} correctly. For Internet Explorer through IE8, there is a
plugin on the web for this purpose which no longer works for IE9.
Other browsers, like Chrome and Safari, will not do this reliably. In LaTeX
(as in texWins) the code on the left also prints the symbol on the right,
and does the curly phi correctly. If you're curious as to why, you can
follows this silly debate among experts on the web. Consult the Advice
pages for more information.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}
The Greeks did know that if additional tools were allowed, for example certain
curves, then trisections became possible. Recall that their rulers were considered
unmarked \textit{straight-edges}. Archimedes, the greatest mathematician and
physicist of the ancient world, showed that if you were allowed to make two
marks on a ruler, it is possible. And all it takes is the EXAT.
In the figure, the given angle is on the right. I have omitted letter labels to
wean you away from such geometric training wheels. Letter labels make it too easy just to check each
item stated. The real world comes without labels, and you should learn to
``read" a figure without them. So, draw a circle about the given angle, and
extend one side of the angle to an entire diameter, and then extend this
diameters as far to the left as needed. Euclids second postulate says that
you can do this. Modern geometry considers all lines to be infinite anyway.
Now mark a segment on a straight-edge equal to the radius of the circle.
Place the marked ruler in such a way that it passes through the end of
the other side of the angle, crosses the circle and lands on the extended
diamater exactly one radius distance further on. In the figure three segments
the length of a radius are marked more heavily. They form the sides of
two isosceles triangles. By \textit{Pons Asinorum} and EXAT applied
two times, the smallest angle is one-third the size of the original angle.
The angle marks help see the relationships.
\section{Symbolic Logic}
An important prerequisite for this course is the symbolic logic and proof theory
you learned in MA347, MA348 or an equivalent course elsewhere. Consider, for instance,
the sentence I used above:
``Coming this early in the text suggests that somehow not being able to supply
the proof, a student is unprepared for the course."
Just what does this mean? Try to reword it by a liberal use of ``ifs" and
``thens". Let's abbreviate three sentences by letters standing for
propositions.
\begin{itemize}
\item A = ``Pons Asinorum comes early in the course."
\item B = ``The student is unable to supply the proof."
\item C = ``The student is unprepared for the course."
\end{itemize}
Recall that a \textit{propositions} is a complete sentence (subject and predicate)
which can be determined to be either true of false. Bertrand Russell's example
``The king of France is bald" is an example of a sentence that is not a proposition.
Can you think of some other examples?
The original sentence can now be rephrased in one of two ways:
\begin{itemize}
\item D = ``Given A, if B then C "
\item E = ``If A and B, then C"
\end{itemize}
Recall from MA347, the ``if X then Y" form is called \textit{material implication}
and may be written as ``X => Y". Recall also that the truth table of => is identical to the
truth table of ``not X or Y". If we rewrite ``D = A => (B=>C)", you should now prove that
D and E are equivalent by the rules of the symbolic logic. Do it!
\section{Filecard}
Please fill out this
Filecard A1 on this lesson.
\section{LaTeX, HTML and Ascii Notation}
In this course we'll use a variety of mathematical notation, all of which presents
problems in writing from the keyboard. For example, in the last paragraph, we typed
=> for $\implies$, which resemble each other well enough. ``not X or Y" is a poor
substitute for $ \ \neg X \ \or \ Y $. Still, the keyboard notation remains readable.
Here we list the notation needed to make this document typographically correct.
As of 9jan12, using augmented ltmml.js, the LaTeX term on the left prints like
the symbol on the right. But only Firefox browsers can interpret a web language called \it{MathML} correctly. For Internet Explorer through IE8, there is a
plugin on the web for this purpose which no longer works for IE9.
Other browsers, like Chrome and Safari, will not do this reliably. In LaTeX
(as in texWins) the code on the left also prints the symbol on the right,
and does the curly phi correctly. If you're curious as to why, you can
follows this silly debate among experts on the web. Consult the Advice
pages for more information.
\begin{eqnarray*}
\mbox{\wedge} & \wedge \\
\mbox{\and} & \and \\
\mbox{\frac12} & \frac12 \\
\mbox{\ell} & \ell \\
\mbox{\pm} & \pm \\
\mbox{\times} & \times \\
\mbox{\cap} & \cap \\
\mbox{\cup} & \cup \\
\mbox{\vee} & \vee \\
\mbox{\or} & \or \\
\mbox{\and} & \and \\
\mbox{\exists} & \exists \\
\mbox{\forall} & \forall \\
\mbox{\equiv} & \equiv \\
\mbox{\setminus} & \setminus \\
\mbox{\sim} & \sim \\
\mbox{\cong} & \cong \\
\mbox{\neg} & \neg \\
\mbox{\in} & \in \\
\mbox{\notin} & \notin \\
\mbox{\subset} & \subset \\
\mbox{\Rightarrow} & \Rightarrow \\
\mbox{\rightarrow} & \rightarrow \\
\mbox{\copyright} & \copyright \\
\mbox{\sum} & \sum \\
\mbox{\int_0^1 } & \int_0^1 \frac{dt}{t} \\
\mbox{\perp} & \perp \\
\mbox{\S}\ =\ section & \S \\
\mbox{\P}\ =\ paragraph& \P \\
\mbox{\emptyset} & \emptyset \\
\mbox{\bot} & \bot \\
\mbox{\varphi} \ =still\ wrong & \varphi \\
\mbox{\mathbb{N}\} = \ natural\ numbers \ & \mathbb{N} \\
\mbox{\mathbb{Z}\} =\ integers \ & \mathbb{Z} \\
\mbox{\mathbb{Q}\} =\ rationals \ & \mathbb{Q} \\
\mbox{\mathbb{R}\} =\ reals \ & \mathbb{R} \\
\mbox{\mathbb{C}\} =\ complex\ numbers\ & \mathbb{C} \\
\end{eqnarray*}
\end{document}