7may11, 24may11, 31may13, 4jan13
\section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation. It thus serves the same purpose
as the first Project 1 of Hvidsten's text, and replaces it.
\subsection{Why we use GEX2.0}
This lesson will help you get started with Michael Hvidsten's
geometry construction package, GEX2.0. The reason we use GEX in MA402
instead of other, similar construction kits, is this. Prof. Hvidsten has
kindly augmented his already superior GEX1.0 which is bundled with his
textbook, to include additional features specifically suited to our course.
\subsection{Who should do this lab.}
This document is intended for all students in the course, but does not
assume that they had the opportunity for a real-time, hands-on and
supervised lab introducing GEX. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GEX as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without verification is bad
science. Thus GEX is useful for discovering geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of
GEX2.0 on your computer. You might also consult his
webpage for operating instructions. Have a pencil and pad of
paper handy when you work through this lab..
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
Our translation:
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Scholars do not really know what Euclid meant by his 4th postulate. Here
we substitute Euclid's Proposition 12 for Postulate E4.
Euclid's celebrated \textit{ Fifth Postulate}, E5, is also known
as \textit{ Euclid's Parallel Postulate}. It is a mouthful. We shall
spend the first third of the course understanding what he had in mind here.
It is the central theme of the course.
We have substituted John Playfair's (*1748) logically equivalent
formulation, E'5, for Euclid's. Later in the course we shall study
this equivalence, and other equivalences, in greater detail.
\textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{GEX Creation versus Construction Buttons}
Note that there are construction buttons on GEX for both E'4 and E'5. Once
you have chosen a line and a point (hold the Shift-Key to choose more than
one object), pressing "perpendicular" or "parallel" constructs that line.
Choosing two points permits you to construct a circle, E'3, or a line segment,
E'1. Do not confuse the construction buttons with advanced creation buttons for
circles, line segments, rays and full lines. The latter are very convenient
shortcuts for creating pairs of points and the constructing the object.
Here is snapshot of the chrome in GEX. Explore each feature and make a note of
it in your Journal with a short review of what is behind each button..
\section{Construction in the Euclidean Plane}
\subsection{Recipe}
\begin{itemize}
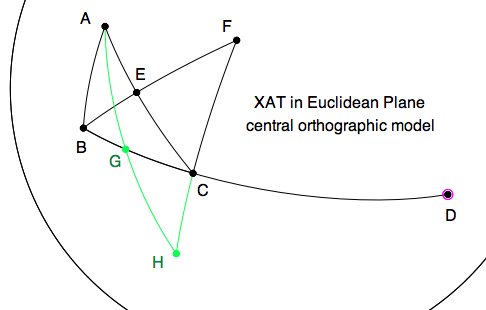
\item X1. Open GEX2.0 $\rightarrow$ EuclModel $\rightarrow$ CentralOrthoModel.
\item X2. Create a $\triangle{ABC}$.
\item X3. Construct the ray extending segment $BC$ beyond $C$.
\item X4. Create a point $D$ on the ray beyond $C$.
\item X5. Bisect side $AC$ at $E$.
\item X6. Double the median $BE$ to $EF$
\item X7. Construct segment $FC$.
\item X8a. Measure and show that $\angle{FCA}=\angle{BAE}$.
\item X8b. Measure and show that $\angle{DCF}=\angle{DCF}$.
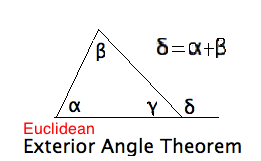
\item X8c. Conclude that \textbf{ in the Euclidean plane, the exterior angle
of a triangle is the sum of the opposite interior angles.}
\item X9. Switch to GEX2.0 $\rightarrow$ EuclModel $\rightarrow$ QuadModel.
\item X10. Record your observations on scratch paper, edit, and enter into
your Journal.
\end{itemize}
\subsection{Comments on the GEX construction}
Note that in the Create-Palette there are buttons to shortcut
some constructions. For example, to draw a triangle (X2),
you can use the rubber-band cursor tool (fourth button in the creation
palette) to draw a closed polygon of three edges.
Note that to draw a triangle, you really only need two tools, the
point creator, and the line-segment constructor. First
\textbf{create} 3 points.
Then choose 2 points and \textbf{construct} a side of the triangle.
Do this three times. Hold the shift-key to choose multiple
objects. Choose an empty spot to reject unwanted choices. In this way,
Hvidsten's buttons play the role of primitives and compound actions. The
latter can be reduced to a sequence of the former. Compare this to
Euclid's postulates and propositions, and the axioms and theorems
of an axiomatic system.
Note that we have used Euclid's first Postulate three time. Apply the
second Postulate by using the ray tool in the Create palette to extend
the base of the triangle (X3). Note how you can \textit{ snap} the
second point of the ray exactly onto $C$. So check that this was
successful, \textit{ wiggle } the figure by choosing (first Create tool)
one of the constructors, for example $C$, and moving it around. If the
ray remains an elongation of $BC$ then your construction was correct.
Similarly, for (X4) snap the point $D$ to the ray. For (X5) you
choose a segment to bisect, and apply the bisection tool. In Euclid's
Elements, it is a theorem that you can do this, not a postulate.
\section{Vocabulary and Review}
\begin{itemize}
\item \textit{Wiggle:} Choose one of the initially \textit{ created}
objects and move them around to see that the rest of the construction
hold together.
\item \textit{ Produce a segment} Choose endpoints of a segment,
mark this vector, choose the segment, translate what's chosen.
\end{itemize}
Here is a more detailed discussion of what you have, or are
about to actually do. Do not worry about how verbose this lesson is
and its redundancy. As you learn how to work with GEX the lesson
will become shorter, terser, and leave a lot more to you.
\begin{enumerate}
\item Be sure you have a working copy of
GEX2.0 on your computer. You might also consult his
webpage for operating instructions. Have a pencil and pad of
paper handy.
\item Take a another look at Euclid's five postulates (Appendix A of
text, or Google them). You might enter them into your Journal for
future reference.
\item. Euclid's formulation shows that he considered his first 3 postulates
to be constructions. Therefore, we want to see how to construct them in the
various models of Euclidean and non-Euclidean geometry available on GEX.
\item Postulate 4 has been a mystery for 2300 years. So we'll ignore
Euclid's formulation for now. But Postulate 5, the Parallel Postulate, is
central to geometry and this course. Euclid's formulation of it is very
strange, and for a good reason. For now we use an equivalent formulation
due to John Playfair (1795). We will also substitute a theorem for E4,
namely, that for a line and a point off the line, there is a unique
perpendicular from the point to the line. Now all five Postulates assert
that a certain construction can be performed.
\item The idea of these experiments is to see HOW these five axioms hold
in the three models of Euclidean geometry in GEX2.0, and whether or not
they hold in the two non-Euclidean geometries.
\item You should familiarize yourself with GEX 2.0, for instance by
working with the appendix in the textbook (which is for GEX 1.0) and the
relevant new parts in the documentation available for GEX 2.0. At this
point we ONLY need the following features:
\item Create Buttons: Euclid specifies that there are points and lines,
and a point can either be on the line or not. So you can Create points.
After every creation step you should immediately pick the Picker a.k.a.
Chooser or the
Arrow button, or you'll continue to create new stuff you'll want to
erase.
\item Given two points (pick two points, holding the shift key down for
the second choice), you can Construct exactly those items that light up
in the Construct menu. For Euclid, the line meant a line segment. Note
that when you have chosen (picked) two points (no more nor less. Shake off
anything accidentally sticking to your picker by picking a blank place.)
the circle construction is also lit up. So you know that E3 is true.
\item Shortcut Creations: Hvidsten provides 4 shortcuts in the Creation
menu. Each of them ends up with a construction based on two points the:
circle, segment, ray, and a full line. The two points mark the beginning
and end position of your tool. Note that a creating point snaps to a another
object if you get it near enough. That is usually a good thing. If it
isn't, undo your action in the Edit menu.
\item Euclidean Models: The EuclModel pulldown menu lets you choose one of
3 models to work in. You can see all three models with the QuadModel
choice. But note, you can continue working ONLY in the chosen one in top
left panel. While experimenting, it is faster to just pick a new canvas
than to try and correct the one you're working in. Don't bother saving
for now. This is scratch paper.
\item Near the end of the course we will discuss how GEX 2.0 does this
work. For now you need to understand that in addition to your usual
idea of the Euclidan plane, as interpreted on a sheet of paper since
your earliest schooling, we have two BOUNDED models, which consist of
the points inside, but NOT on the boundary of a disk. We show the
boundary for reference, but in this interpretation, all the Points are
inside the disk.
\item When discussing models of geometrical axiom systems, it is
\texbf{essential} to distinguish between the names of objects in our common
idea of a the plane (the points, lines, parallels, perpendiculars, circles
you've used since you were wee children) and those geometrical figures
that interpret the primitives of our axiom systems. We will capitalize
words referring to the latter. It might be nicer to use color, and even
musical jingles to alert you to this use of the same English words to
mean two different things, or even use a foreign language. But all that
is impractical. You have good brains and soon will have no difficulty
keeping this straight.
\end{enumerate}
\section{Some final advice}
Do not admit to being \textit{confused} by this lesson . It's OK
to not quite understand all of it in one sitting. Use a knife and fork, and
maybe keep some left-overs in the fridge for later. Take your time. But
do not allow yourself to be confused. Befuddlement is for the ignorant
or the lazy. In fact, we'll spend the entire semester really understanding
these concepts. Right now we're learning by using, like the mother
tongue babies learn by experience.
\section{Lab Report}
Your report on this lab should be a 2-4 page write up in .pdf format (15pc).
There should be to be at least two properly captioned figures (15pc).
Be sure that all mathematical formulas and letters are in LaTeX format
(dollar signs!). There should be at least two mathematical formulas (15pc).
Geometrical accuracy and expository quality counts for half the grade.
\begin{itemize}
\item Compose your lab report as a draft first.
\item Draw hand sketches of what you plan to illustrate.
\item Practice the LaTeX formulas you'll use in texPad first.
\item Complete your figures in GEX2.0. Save your .gex files on your computer where you can find it easily.
\item Make screen print of the figures. Edit them Paint/iPaint or some other picture editor if needed. Then upload your figures into texWins.
\item Compose your report on texWins. Save a copy of your workspace on your
computer. Be sure to change its generic name "mywspace.tex" to something that shows it belongs to you. Do NOT use spaces in the name!
\item Download the .pdf, change its generic name "texdoc.pdf" to something more
recognizable and upload it into the Moodle.
\end{itemize}
The following is a sequel to this lab. At a later
date specified in the syllabus you should resume this experiment here.
Lab on the Exterior Angle Theorem (XAT) with Geometry Explorer (GEX2.0)
Part I: In the Euclidean Plane
\begin{document} \maketitle
\section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation. It thus serves the same purpose
as the first Project 1 of Hvidsten's text, and replaces it.
\subsection{Why we use GEX2.0}
This lesson will help you get started with Michael Hvidsten's
geometry construction package, GEX2.0. The reason we use GEX in MA402
instead of other, similar construction kits, is this. Prof. Hvidsten has
kindly augmented his already superior GEX1.0 which is bundled with his
textbook, to include additional features specifically suited to our course.
\subsection{Who should do this lab.}
This document is intended for all students in the course, but does not
assume that they had the opportunity for a real-time, hands-on and
supervised lab introducing GEX. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GEX as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without verification is bad
science. Thus GEX is useful for discovering geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of
GEX2.0 on your computer. You might also consult his
webpage for operating instructions. Have a pencil and pad of
paper handy when you work through this lab..
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
Our translation:
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Scholars do not really know what Euclid meant by his 4th postulate. Here
we substitute Euclid's Proposition 12 for Postulate E4.
Euclid's celebrated \textit{ Fifth Postulate}, E5, is also known
as \textit{ Euclid's Parallel Postulate}. It is a mouthful. We shall
spend the first third of the course understanding what he had in mind here.
It is the central theme of the course.
We have substituted John Playfair's (*1748) logically equivalent
formulation, E'5, for Euclid's. Later in the course we shall study
this equivalence, and other equivalences, in greater detail.
\textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{GEX Creation versus Construction Buttons}
Note that there are construction buttons on GEX for both E'4 and E'5. Once
you have chosen a line and a point (hold the Shift-Key to choose more than
one object), pressing "perpendicular" or "parallel" constructs that line.
Choosing two points permits you to construct a circle, E'3, or a line segment,
E'1. Do not confuse the construction buttons with advanced creation buttons for
circles, line segments, rays and full lines. The latter are very convenient
shortcuts for creating pairs of points and the constructing the object.
Here is snapshot of the chrome in GEX. Explore each feature and make a note of
it in your Journal with a short review of what is behind each button..
\section{Construction in the Euclidean Plane}
\subsection{Recipe}
\begin{itemize}
\item X1. Open GEX2.0 $\rightarrow$ EuclModel $\rightarrow$ CentralOrthoModel.
\item X2. Create a $\triangle{ABC}$.
\item X3. Construct the ray extending segment $BC$ beyond $C$.
\item X4. Create a point $D$ on the ray beyond $C$.
\item X5. Bisect side $AC$ at $E$.
\item X6. Double the median $BE$ to $EF$
\item X7. Construct segment $FC$.
\item X8a. Measure and show that $\angle{FCA}=\angle{BAE}$.
\item X8b. Measure and show that $\angle{DCF}=\angle{DCF}$.
\item X8c. Conclude that \textbf{ in the Euclidean plane, the exterior angle
of a triangle is the sum of the opposite interior angles.}
\item X9. Switch to GEX2.0 $\rightarrow$ EuclModel $\rightarrow$ QuadModel.
\item X10. Record your observations on scratch paper, edit, and enter into
your Journal.
\end{itemize}
\subsection{Comments on the GEX construction}
Note that in the Create-Palette there are buttons to shortcut
some constructions. For example, to draw a triangle (X2),
you can use the rubber-band cursor tool (fourth button in the creation
palette) to draw a closed polygon of three edges.
Note that to draw a triangle, you really only need two tools, the
point creator, and the line-segment constructor. First
\textbf{create} 3 points.
Then choose 2 points and \textbf{construct} a side of the triangle.
Do this three times. Hold the shift-key to choose multiple
objects. Choose an empty spot to reject unwanted choices. In this way,
Hvidsten's buttons play the role of primitives and compound actions. The
latter can be reduced to a sequence of the former. Compare this to
Euclid's postulates and propositions, and the axioms and theorems
of an axiomatic system.
Note that we have used Euclid's first Postulate three time. Apply the
second Postulate by using the ray tool in the Create palette to extend
the base of the triangle (X3). Note how you can \textit{ snap} the
second point of the ray exactly onto $C$. So check that this was
successful, \textit{ wiggle } the figure by choosing (first Create tool)
one of the constructors, for example $C$, and moving it around. If the
ray remains an elongation of $BC$ then your construction was correct.
Similarly, for (X4) snap the point $D$ to the ray. For (X5) you
choose a segment to bisect, and apply the bisection tool. In Euclid's
Elements, it is a theorem that you can do this, not a postulate.
Question 1.
Look in the back of Hvidsten, or google Euclid's first book, and find
the Proposition saying that segments can be bisected.
To double the median (X6) with a ruler and compass would be quite easy.
You apply the ruler to produce the median, the compass to measure
off the distance, and mark off the new point.
Question 2.
Simulate this ruler-and-compass costruction in GEX by using the
Ray-creator, and the Circle-constructor. To extend a segment create the
ray through the endpoints of the segment. Then use a circle of the right
center and radius to mark off the new point. For this you use the
Intersection-constructor. Write here that you have completed the construction.
We shall use a different, initially less intuitive construction, but one
that has many dividends later in the the course. Do this
\begin{itemize}
\item V1. Choose the points $B$ and $E$ in that order. Click on \textit{ Mark}
in the \textit{ Transform} palette. Choose \textit{ Vector}, in
\textit{rectangular} coordinates. Henceforth, this construction shall be
referred to simply as \texit{mark vector}$\vec{BE}$.
\item V2. Once a transformation has been \textit{marked}, it can be applied to
any parts of the existing figure. Here, choose the median $BE$ and the
midpoint $E$ and \textit{ translate it} (1st button in Transform palette).
\end{itemize}
Henceforth we shall refer to the foregoing construction as \textit{producing the segment} to one-side of itself or the other.
To measure an angle, for example $\angle{ FCE}$, choose the points
\textit{ in this order} because that is the positive (counterclockwise)
orientation for a positive angle. Then pull down the $Measure$ tab in
the GEX chrome.
\subsection{Vector Notation}
We have used the conventional notation $BE$ for a \textit{directed
line segment} with initial poit $B$ and final point $E$. In the
prerequisite calculus course you learned that the set of all such
segments parallel to the given segment comprises the \textit{vector}
$\vec{BE}$. And here you have observed how a vector determines a
transformation called a \textit{translation.} The line through
two point $B$ and $E$ for example, is sometimes written as $\ell_{BE}$.
Here the order is not important, $\ell_{BE}=\ell_{EB}$.
But both
notations, the over-arrow and the curly-ell with a subscript is
inconvenient to write in a text document not specifically designed for it,
as is LaTeX. Besides it takes an effort to write this on paper, and can't
be written into an email. So we will abandon both notations. The line
determined by two points will be writte $(EB)$. And the vector determined
by the two points is written $B-E$, the difference of two points. Note the reversal of
the order required by vector algebra. The segment in a figure can continue
to be written just $BE$, as it has been for two millennia.
Here is a little comic-strip on what
we have been talking about here.
\subsection{Geometrical Commentary}
GEX2.0 allows us to break the lifelong habit of seeing the Euclidean plane
in only one way, the way you were taught since grade school. C-Students in
this course frequently answer the question, "What is non-Euclidean geometry?"
something like this:
"In non-Euclidean there are points and straight lines, except that they
are not straight but curved."
Using some 3-D geometries we shall study later, we can have a model of
the Euclidean plane in which the straight lines are also curved. And
we shall see models of the non-Euclidean plane in which the straight
lines look straight to our Euclidean eyes.
Now, Euclid would not have accepted the above argument simulated by
GEX because the Greeks had no numerical sense of measuring angles.
They could compare angles, but not by associating numbers to them.
Even we should not trust a mere machine to have measured the angles
to the very last decimal place. That is why geometry is a deductive science.
This is a very good thing, because as we shall see in the second
exercise, things are different in non-Euclidean Geometry.
\section{Vocabulary and Review}
\begin{itemize}
\item \textit{Wiggle:} Choose one of the initially \textit{ created}
objects and move them around to see that the rest of the construction
hold together.
\item \textit{ Produce a segment} Choose endpoints of a segment,
mark this vector, choose the segment, translate what's chosen.
\end{itemize}
Here is a more detailed discussion of what you have, or are
about to actually do. Do not worry about how verbose this lesson is
and its redundancy. As you learn how to work with GEX the lesson
will become shorter, terser, and leave a lot more to you.
\begin{enumerate}
\item Be sure you have a working copy of
GEX2.0 on your computer. You might also consult his
webpage for operating instructions. Have a pencil and pad of
paper handy.
\item Take a another look at Euclid's five postulates (Appendix A of
text, or Google them). You might enter them into your Journal for
future reference.
\item. Euclid's formulation shows that he considered his first 3 postulates
to be constructions. Therefore, we want to see how to construct them in the
various models of Euclidean and non-Euclidean geometry available on GEX.
\item Postulate 4 has been a mystery for 2300 years. So we'll ignore
Euclid's formulation for now. But Postulate 5, the Parallel Postulate, is
central to geometry and this course. Euclid's formulation of it is very
strange, and for a good reason. For now we use an equivalent formulation
due to John Playfair (1795). We will also substitute a theorem for E4,
namely, that for a line and a point off the line, there is a unique
perpendicular from the point to the line. Now all five Postulates assert
that a certain construction can be performed.
\item The idea of these experiments is to see HOW these five axioms hold
in the three models of Euclidean geometry in GEX2.0, and whether or not
they hold in the two non-Euclidean geometries.
\item You should familiarize yourself with GEX 2.0, for instance by
working with the appendix in the textbook (which is for GEX 1.0) and the
relevant new parts in the documentation available for GEX 2.0. At this
point we ONLY need the following features:
\item Create Buttons: Euclid specifies that there are points and lines,
and a point can either be on the line or not. So you can Create points.
After every creation step you should immediately pick the Picker a.k.a.
Chooser or the
Arrow button, or you'll continue to create new stuff you'll want to
erase.
\item Given two points (pick two points, holding the shift key down for
the second choice), you can Construct exactly those items that light up
in the Construct menu. For Euclid, the line meant a line segment. Note
that when you have chosen (picked) two points (no more nor less. Shake off
anything accidentally sticking to your picker by picking a blank place.)
the circle construction is also lit up. So you know that E3 is true.
\item Shortcut Creations: Hvidsten provides 4 shortcuts in the Creation
menu. Each of them ends up with a construction based on two points the:
circle, segment, ray, and a full line. The two points mark the beginning
and end position of your tool. Note that a creating point snaps to a another
object if you get it near enough. That is usually a good thing. If it
isn't, undo your action in the Edit menu.
\item Euclidean Models: The EuclModel pulldown menu lets you choose one of
3 models to work in. You can see all three models with the QuadModel
choice. But note, you can continue working ONLY in the chosen one in top
left panel. While experimenting, it is faster to just pick a new canvas
than to try and correct the one you're working in. Don't bother saving
for now. This is scratch paper.
\item Near the end of the course we will discuss how GEX 2.0 does this
work. For now you need to understand that in addition to your usual
idea of the Euclidan plane, as interpreted on a sheet of paper since
your earliest schooling, we have two BOUNDED models, which consist of
the points inside, but NOT on the boundary of a disk. We show the
boundary for reference, but in this interpretation, all the Points are
inside the disk.
\item When discussing models of geometrical axiom systems, it is
\texbf{essential} to distinguish between the names of objects in our common
idea of a the plane (the points, lines, parallels, perpendiculars, circles
you've used since you were wee children) and those geometrical figures
that interpret the primitives of our axiom systems. We will capitalize
words referring to the latter. It might be nicer to use color, and even
musical jingles to alert you to this use of the same English words to
mean two different things, or even use a foreign language. But all that
is impractical. You have good brains and soon will have no difficulty
keeping this straight.
\end{enumerate}
\section{Some final advice}
Do not admit to being \textit{confused} by this lesson . It's OK
to not quite understand all of it in one sitting. Use a knife and fork, and
maybe keep some left-overs in the fridge for later. Take your time. But
do not allow yourself to be confused. Befuddlement is for the ignorant
or the lazy. In fact, we'll spend the entire semester really understanding
these concepts. Right now we're learning by using, like the mother
tongue babies learn by experience.
\section{Lab Report}
Your report on this lab should be a 2-4 page write up in .pdf format (15pc).
There should be to be at least two properly captioned figures (15pc).
Be sure that all mathematical formulas and letters are in LaTeX format
(dollar signs!). There should be at least two mathematical formulas (15pc).
Geometrical accuracy and expository quality counts for half the grade.
\begin{itemize}
\item Compose your lab report as a draft first.
\item Draw hand sketches of what you plan to illustrate.
\item Practice the LaTeX formulas you'll use in texPad first.
\item Complete your figures in GEX2.0. Save your .gex files on your computer where you can find it easily.
\item Make screen print of the figures. Edit them Paint/iPaint or some other picture editor if needed. Then upload your figures into texWins.
\item Compose your report on texWins. Save a copy of your workspace on your
computer. Be sure to change its generic name "mywspace.tex" to something that shows it belongs to you. Do NOT use spaces in the name!
\item Download the .pdf, change its generic name "texdoc.pdf" to something more
recognizable and upload it into the Moodle.
\end{itemize}
The following is a sequel to this lab. At a later
date specified in the syllabus you should resume this experiment here.