25jan15
 \section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation using a computer based geometric
contruction package, GeoGebra (GGB). The associated video also tells you how to
download GGB and use enough of its features for present purposes. You are
encouraged to explore GGB further using its extensive online help, both
tutorials and videos. We will review those features needed at the time.
This document is intended for all students in the course, but does not
assume that you had the opportunity for a real-time, hands-on and
supervised lab introducing GGB. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab. It is due at a much later time than the Filecard
questions embedding in this lesson.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GGB as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without theoretical
verification is bad science. Thus GGB is useful for discovering
geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of GGB on your own computer.
Always have a pencil and pad of paper handy when you work through
this lab.
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
A modern translation often used in high schools is this.
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Our version, E'4 is actually a Proposition 12 Euclid's Elements, but his
proof of it would not be valid by today's standards. Note how different
Euclid's E5 is from our E'5 by John Playfair (*1748). We will devote an
entire chapter of our course to the equivalence of these two, and many
more formulations of the same concept. We refer to E5
as \textit{Euclid's Fifths Postulate} and E'5 as \textit{Playfair's Axiom}.
\section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation using a computer based geometric
contruction package, GeoGebra (GGB). The associated video also tells you how to
download GGB and use enough of its features for present purposes. You are
encouraged to explore GGB further using its extensive online help, both
tutorials and videos. We will review those features needed at the time.
This document is intended for all students in the course, but does not
assume that you had the opportunity for a real-time, hands-on and
supervised lab introducing GGB. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab. It is due at a much later time than the Filecard
questions embedding in this lesson.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GGB as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without theoretical
verification is bad science. Thus GGB is useful for discovering
geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of GGB on your own computer.
Always have a pencil and pad of paper handy when you work through
this lab.
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
A modern translation often used in high schools is this.
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Our version, E'4 is actually a Proposition 12 Euclid's Elements, but his
proof of it would not be valid by today's standards. Note how different
Euclid's E5 is from our E'5 by John Playfair (*1748). We will devote an
entire chapter of our course to the equivalence of these two, and many
more formulations of the same concept. We refer to E5
as \textit{Euclid's Fifths Postulate} and E'5 as \textit{Playfair's Axiom}.
 \textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{Creation Tools versus Construction Tools }
Note that GGB has many tools for constructing geometrical figures. All
but a few depend on your choice of points in the plane. Although Markus
Hohenwarter, the author of GGB, does not distinguish as carefully as we
could wish between these, we shall do for the purposes of our course.
\textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{Creation Tools versus Construction Tools }
Note that GGB has many tools for constructing geometrical figures. All
but a few depend on your choice of points in the plane. Although Markus
Hohenwarter, the author of GGB, does not distinguish as carefully as we
could wish between these, we shall do for the purposes of our course.
 Here is the list of pull-down menus in the top chrome of GGB. Below that are the Tool Buttons
in the chrome of the drawing window. We leave the pulldown menus in the former to your investigation.
Here we just show you the tools under the buttons.
The Fat Arrow tool is
for grabbing and pointing to objects in your evolving construction. When you're finished
with a construction, immediately choose the Fat Arrow, or the next click will produce an
unwanted object which you will have to erase (Chrome>Edit>Undo, or CTL-Z).
All constructions begin with points in the plane. To place points use the Point Tool. Use
the Fat Arrow to move them to a different place, if you like. But there are more instances
when points are created, and these are served by the other Point Tools in the pull-down
menu.
Here is the list of pull-down menus in the top chrome of GGB. Below that are the Tool Buttons
in the chrome of the drawing window. We leave the pulldown menus in the former to your investigation.
Here we just show you the tools under the buttons.
The Fat Arrow tool is
for grabbing and pointing to objects in your evolving construction. When you're finished
with a construction, immediately choose the Fat Arrow, or the next click will produce an
unwanted object which you will have to erase (Chrome>Edit>Undo, or CTL-Z).
All constructions begin with points in the plane. To place points use the Point Tool. Use
the Fat Arrow to move them to a different place, if you like. But there are more instances
when points are created, and these are served by the other Point Tools in the pull-down
menu.
 For a start we only need two of these: the Intersect and the Midpoint tools. It didn't even
occur to Euclid that there might not be a point where two curves appear to cross. So, it is
appropriate that we have a special button for this. Similarly, Euclid constructed the
midpoint of a line-segment in his Elements. Perhaps you remember how to do it with a
ruler and compass. But we'll accept these as given construction tools.
To find the midpoint of the segment first choose the Midpoint tool, then the two points.
Similarly, for the intersection of two curves, first choose the Intersect tool, then
the two curves. We will not mention this sequence again, so remember it. First decide
what it is you wan to construct. Then identify the givens needed to do it. The button
will remind you of this yoga.
For a start we only need two of these: the Intersect and the Midpoint tools. It didn't even
occur to Euclid that there might not be a point where two curves appear to cross. So, it is
appropriate that we have a special button for this. Similarly, Euclid constructed the
midpoint of a line-segment in his Elements. Perhaps you remember how to do it with a
ruler and compass. But we'll accept these as given construction tools.
To find the midpoint of the segment first choose the Midpoint tool, then the two points.
Similarly, for the intersection of two curves, first choose the Intersect tool, then
the two curves. We will not mention this sequence again, so remember it. First decide
what it is you wan to construct. Then identify the givens needed to do it. The button
will remind you of this yoga.
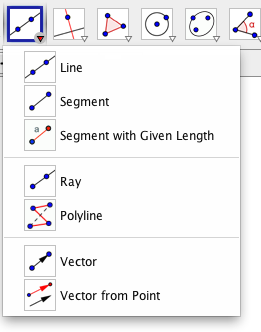 Similarely, the Line Tool embodies Euclid's first postulate. Two points determine a line.
Remember, for Euclid this meant what we now call a "line segment". Don't forget, however,
that every line is infinite in both directions, even if we don't always draw them that
way. Again, there are only two further line tools we want, the segment, and the ray.
For the ray you must name the points in the "tail to tip" order, which your are used to
from the vector calculus.
Similarely, the Line Tool embodies Euclid's first postulate. Two points determine a line.
Remember, for Euclid this meant what we now call a "line segment". Don't forget, however,
that every line is infinite in both directions, even if we don't always draw them that
way. Again, there are only two further line tools we want, the segment, and the ray.
For the ray you must name the points in the "tail to tip" order, which your are used to
from the vector calculus.
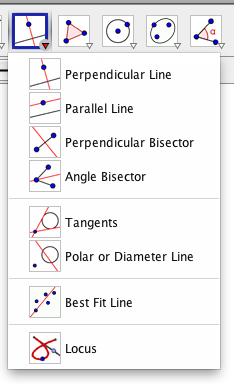 We won't need the tools that depend on a point and a line, such as the perpendicular, the
parallel, and perpendicular bisector. But these three will come in handy in the future.
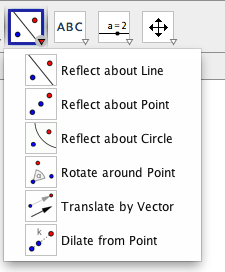
Finally, the most important tools in geometry are those that implement transformations
as they apply to objects in a construction. For this lesson we will only need the
Translation tool. Unfortunately, to be consistent Hohenwarter requires you to first
choose what you want to translate, and the then the vector that defines the translation.
We won't need the tools that depend on a point and a line, such as the perpendicular, the
parallel, and perpendicular bisector. But these three will come in handy in the future.
Finally, the most important tools in geometry are those that implement transformations
as they apply to objects in a construction. For this lesson we will only need the
Translation tool. Unfortunately, to be consistent Hohenwarter requires you to first
choose what you want to translate, and the then the vector that defines the translation.
 That takes a little getting used to.
But what about the compass in the ruler-and-compass constructions of Euclid? We'll need the
Circle Tool that depends on the center (first) and then a radius (second) given by a point
on the circle. That's pretty easy. But you may shudder to remember how many steps it took
to construct a circle through any three non-collinear points. GGB has a button for that too.
\section{Construction in the Euclidean Plane}
That takes a little getting used to.
But what about the compass in the ruler-and-compass constructions of Euclid? We'll need the
Circle Tool that depends on the center (first) and then a radius (second) given by a point
on the circle. That's pretty easy. But you may shudder to remember how many steps it took
to construct a circle through any three non-collinear points. GGB has a button for that too.
\section{Construction in the Euclidean Plane}
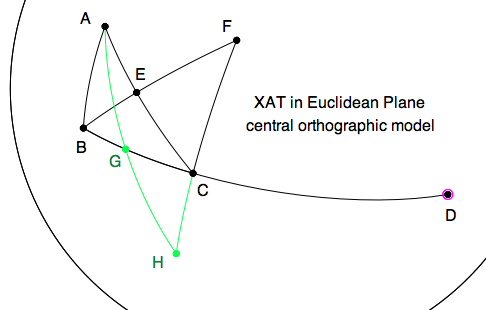
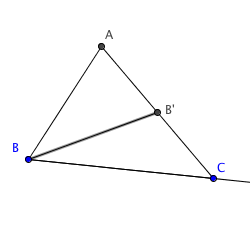 We are now ready to use these tools to construct a figure illustrating the Exterior
Angle Theorem.
First construct the median of a given triangle (the line joining a vertex like $B$ to
the midpoint of the opposite side $B'$. The Midpoint Button and the Segment Button
suffice, after you have chosen the three vertices of $\triangle ABC$. Note we also
used the Ray Button to create the Exterior Angle at C, $ext \angle C$.
We are now ready to use these tools to construct a figure illustrating the Exterior
Angle Theorem.
First construct the median of a given triangle (the line joining a vertex like $B$ to
the midpoint of the opposite side $B'$. The Midpoint Button and the Segment Button
suffice, after you have chosen the three vertices of $\triangle ABC$. Note we also
used the Ray Button to create the Exterior Angle at C, $ext \angle C$.
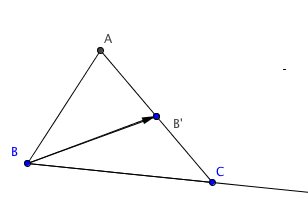
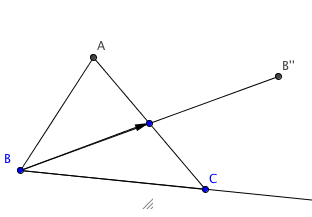 Here we will translate the median along itself in order to double it outside the
triangle. After choosing the median $BB'$ and choose it again as the translation vectore
we get to $B''$. This figure can be constructed with ruler and compass too.
Finally, connecting $B''$ to $C$ finishes the figure.
Here we will translate the median along itself in order to double it outside the
triangle. After choosing the median $BB'$ and choose it again as the translation vectore
we get to $B''$. This figure can be constructed with ruler and compass too.
Finally, connecting $B''$ to $C$ finishes the figure.
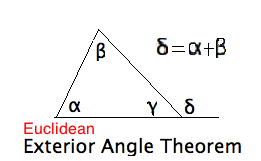
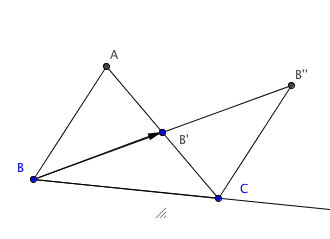 Recall that $\angle BAC \cong \angle CB'' B'$ follows by SAS to prove that
$\triangle BAC \cong \triangle CB'' B'$. This is the \txtbf{Absolute Exterior Angle Theorem} AXAT.
Of course, since we drew it in the Euclidean plane, we can also read off the
Euclidean Exterior Angle Theorem (EXAT) but we'll come to that in much later lessons.
\end{document}
Recall that $\angle BAC \cong \angle CB'' B'$ follows by SAS to prove that
$\triangle BAC \cong \triangle CB'' B'$. This is the \txtbf{Absolute Exterior Angle Theorem} AXAT.
Of course, since we drew it in the Euclidean plane, we can also read off the
Euclidean Exterior Angle Theorem (EXAT) but we'll come to that in much later lessons.
\end{document}
Lab on the Exterior Angle Theorem (XAT) with Geogebra (GGB)
Part I: In the Euclidean Plane
\begin{document} \maketitle \section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation using a computer based geometric
contruction package, GeoGebra (GGB). The associated video also tells you how to
download GGB and use enough of its features for present purposes. You are
encouraged to explore GGB further using its extensive online help, both
tutorials and videos. We will review those features needed at the time.
This document is intended for all students in the course, but does not
assume that you had the opportunity for a real-time, hands-on and
supervised lab introducing GGB. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab. It is due at a much later time than the Filecard
questions embedding in this lesson.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GGB as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without theoretical
verification is bad science. Thus GGB is useful for discovering
geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of GGB on your own computer.
Always have a pencil and pad of paper handy when you work through
this lab.
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
A modern translation often used in high schools is this.
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Our version, E'4 is actually a Proposition 12 Euclid's Elements, but his
proof of it would not be valid by today's standards. Note how different
Euclid's E5 is from our E'5 by John Playfair (*1748). We will devote an
entire chapter of our course to the equivalence of these two, and many
more formulations of the same concept. We refer to E5
as \textit{Euclid's Fifths Postulate} and E'5 as \textit{Playfair's Axiom}.
\section{Introduction}
This lesson explores the differences between Euclidean and non-Euclidean
geometry by means of experimentation using a computer based geometric
contruction package, GeoGebra (GGB). The associated video also tells you how to
download GGB and use enough of its features for present purposes. You are
encouraged to explore GGB further using its extensive online help, both
tutorials and videos. We will review those features needed at the time.
This document is intended for all students in the course, but does not
assume that you had the opportunity for a real-time, hands-on and
supervised lab introducing GGB. The Lab Report section below addresses
the problem of providing feedback to your instructor that you have
completed this lab. It is due at a much later time than the Filecard
questions embedding in this lesson.
The style of this and subsequent labs is best compared to a recipe in
a cookbook. First a list of "ingredients" followed by elaboration which
may or may not be useful.
\subsection{Geometrical significance.}
As Hvidsten points out, contemporary college students need an experiential
referent for axiomatic geometry. This is the more true the fewer students
have had a rigorous treatment of Euclid's Postulates and their
consequences in high school. We may think of the GGB as a simulation of
of an axiomatic system. There are \textit{ primitives}, sometimes also
called \textit{ undefined terms}, such as \textit{ points, lines}
and the relation of \textit{incidence}. There are elementary
\textit{ constructions} accessed by button presses. These may be
treated as \textit{ axioms} and subsequent constructions you make are
the \textit{ theorems}.
But you must never forget that experiment without theoretical
verification is bad science. Thus GGB is useful for discovering
geometrical facts, and
testing geometrical conjectures. The proof, however, proceeds in a
more mathematical manner.
\section{Experiment A: Euclid's Postulates}
In the first experiment we examine Eulid's five Postulates, rephrase
a few, and examine their validity in several models of the
Euclidean and non-Euclidean plane.
Be sure you have a working copy of GGB on your own computer.
Always have a pencil and pad of paper handy when you work through
this lab.
\subsection{The Postulates}
Here are Euclid's postulates. See also the Appendix A of Hvidsten, and
David Joyce's webpage on
Euclid's Elements.
\begin{itemize}
\item E1: To draw a straight line from any point to any point.
\item E2: To produce a finite straight line continuously in a straight line.
\item E3: To describe a circle with any center and distance.
\item E4: That all right angles are equal to one another.
\item E5: That, if a straight line falling on two straight lines makes the
interior angles on the same side less than two right angles, the
two straight lines, if produced indefinitely, meet on the
side side on which are the angles less than two right angles.
\end{itemize}
A modern translation often used in high schools is this.
\begin{itemize}
\item E'1: Two points determine a (unique) line (segment) between them.
\item E'2: This segment lies on an infinite line.
\item E'3: Draw a circle with given a radius (center and point on circle).
\item E'4: (Perpendiculars) From any point to any line drop the perpendicular.
\item E'5: (Playfair's Postulate). Given a line and a point not on the
line there is a unique line through the point parallel to
the given line. (Lines with no common points are called parallel.)
\end{itemize}
\subsection{Comment on our version of Euclid's Postulates}
Our version, E'4 is actually a Proposition 12 Euclid's Elements, but his
proof of it would not be valid by today's standards. Note how different
Euclid's E5 is from our E'5 by John Playfair (*1748). We will devote an
entire chapter of our course to the equivalence of these two, and many
more formulations of the same concept. We refer to E5
as \textit{Euclid's Fifths Postulate} and E'5 as \textit{Playfair's Axiom}.
 \textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{Creation Tools versus Construction Tools }
Note that GGB has many tools for constructing geometrical figures. All
but a few depend on your choice of points in the plane. Although Markus
Hohenwarter, the author of GGB, does not distinguish as carefully as we
could wish between these, we shall do for the purposes of our course.
\textbf{Vocabulary Exercise: } Euclid uses a number of technical terms in his postlulates,
like \textit{draw, produce continuously, describe, equal, falling}. You
should think about what they meant to his contemporary Greeks 2300 years ago.
Compare this to what they mean in the Geometry Explorer application.
Write an essay on this subject into your Journal.
\subsection{Creation Tools versus Construction Tools }
Note that GGB has many tools for constructing geometrical figures. All
but a few depend on your choice of points in the plane. Although Markus
Hohenwarter, the author of GGB, does not distinguish as carefully as we
could wish between these, we shall do for the purposes of our course.
 Here is the list of pull-down menus in the top chrome of GGB. Below that are the Tool Buttons
in the chrome of the drawing window. We leave the pulldown menus in the former to your investigation.
Here we just show you the tools under the buttons.
The Fat Arrow tool is
for grabbing and pointing to objects in your evolving construction. When you're finished
with a construction, immediately choose the Fat Arrow, or the next click will produce an
unwanted object which you will have to erase (Chrome>Edit>Undo, or CTL-Z).
All constructions begin with points in the plane. To place points use the Point Tool. Use
the Fat Arrow to move them to a different place, if you like. But there are more instances
when points are created, and these are served by the other Point Tools in the pull-down
menu.
Here is the list of pull-down menus in the top chrome of GGB. Below that are the Tool Buttons
in the chrome of the drawing window. We leave the pulldown menus in the former to your investigation.
Here we just show you the tools under the buttons.
The Fat Arrow tool is
for grabbing and pointing to objects in your evolving construction. When you're finished
with a construction, immediately choose the Fat Arrow, or the next click will produce an
unwanted object which you will have to erase (Chrome>Edit>Undo, or CTL-Z).
All constructions begin with points in the plane. To place points use the Point Tool. Use
the Fat Arrow to move them to a different place, if you like. But there are more instances
when points are created, and these are served by the other Point Tools in the pull-down
menu.
 For a start we only need two of these: the Intersect and the Midpoint tools. It didn't even
occur to Euclid that there might not be a point where two curves appear to cross. So, it is
appropriate that we have a special button for this. Similarly, Euclid constructed the
midpoint of a line-segment in his Elements. Perhaps you remember how to do it with a
ruler and compass. But we'll accept these as given construction tools.
To find the midpoint of the segment first choose the Midpoint tool, then the two points.
Similarly, for the intersection of two curves, first choose the Intersect tool, then
the two curves. We will not mention this sequence again, so remember it. First decide
what it is you wan to construct. Then identify the givens needed to do it. The button
will remind you of this yoga.
For a start we only need two of these: the Intersect and the Midpoint tools. It didn't even
occur to Euclid that there might not be a point where two curves appear to cross. So, it is
appropriate that we have a special button for this. Similarly, Euclid constructed the
midpoint of a line-segment in his Elements. Perhaps you remember how to do it with a
ruler and compass. But we'll accept these as given construction tools.
To find the midpoint of the segment first choose the Midpoint tool, then the two points.
Similarly, for the intersection of two curves, first choose the Intersect tool, then
the two curves. We will not mention this sequence again, so remember it. First decide
what it is you wan to construct. Then identify the givens needed to do it. The button
will remind you of this yoga.
 Similarely, the Line Tool embodies Euclid's first postulate. Two points determine a line.
Remember, for Euclid this meant what we now call a "line segment". Don't forget, however,
that every line is infinite in both directions, even if we don't always draw them that
way. Again, there are only two further line tools we want, the segment, and the ray.
For the ray you must name the points in the "tail to tip" order, which your are used to
from the vector calculus.
Similarely, the Line Tool embodies Euclid's first postulate. Two points determine a line.
Remember, for Euclid this meant what we now call a "line segment". Don't forget, however,
that every line is infinite in both directions, even if we don't always draw them that
way. Again, there are only two further line tools we want, the segment, and the ray.
For the ray you must name the points in the "tail to tip" order, which your are used to
from the vector calculus.
 We won't need the tools that depend on a point and a line, such as the perpendicular, the
parallel, and perpendicular bisector. But these three will come in handy in the future.
Finally, the most important tools in geometry are those that implement transformations
as they apply to objects in a construction. For this lesson we will only need the
Translation tool. Unfortunately, to be consistent Hohenwarter requires you to first
choose what you want to translate, and the then the vector that defines the translation.
We won't need the tools that depend on a point and a line, such as the perpendicular, the
parallel, and perpendicular bisector. But these three will come in handy in the future.
Finally, the most important tools in geometry are those that implement transformations
as they apply to objects in a construction. For this lesson we will only need the
Translation tool. Unfortunately, to be consistent Hohenwarter requires you to first
choose what you want to translate, and the then the vector that defines the translation.
 That takes a little getting used to.
But what about the compass in the ruler-and-compass constructions of Euclid? We'll need the
Circle Tool that depends on the center (first) and then a radius (second) given by a point
on the circle. That's pretty easy. But you may shudder to remember how many steps it took
to construct a circle through any three non-collinear points. GGB has a button for that too.
\section{Construction in the Euclidean Plane}
That takes a little getting used to.
But what about the compass in the ruler-and-compass constructions of Euclid? We'll need the
Circle Tool that depends on the center (first) and then a radius (second) given by a point
on the circle. That's pretty easy. But you may shudder to remember how many steps it took
to construct a circle through any three non-collinear points. GGB has a button for that too.
\section{Construction in the Euclidean Plane}
 We are now ready to use these tools to construct a figure illustrating the Exterior
Angle Theorem.
First construct the median of a given triangle (the line joining a vertex like $B$ to
the midpoint of the opposite side $B'$. The Midpoint Button and the Segment Button
suffice, after you have chosen the three vertices of $\triangle ABC$. Note we also
used the Ray Button to create the Exterior Angle at C, $ext \angle C$.
We are now ready to use these tools to construct a figure illustrating the Exterior
Angle Theorem.
First construct the median of a given triangle (the line joining a vertex like $B$ to
the midpoint of the opposite side $B'$. The Midpoint Button and the Segment Button
suffice, after you have chosen the three vertices of $\triangle ABC$. Note we also
used the Ray Button to create the Exterior Angle at C, $ext \angle C$.

 Here we will translate the median along itself in order to double it outside the
triangle. After choosing the median $BB'$ and choose it again as the translation vectore
we get to $B''$. This figure can be constructed with ruler and compass too.
Finally, connecting $B''$ to $C$ finishes the figure.
Here we will translate the median along itself in order to double it outside the
triangle. After choosing the median $BB'$ and choose it again as the translation vectore
we get to $B''$. This figure can be constructed with ruler and compass too.
Finally, connecting $B''$ to $C$ finishes the figure.
 Recall that $\angle BAC \cong \angle CB'' B'$ follows by SAS to prove that
$\triangle BAC \cong \triangle CB'' B'$. This is the \txtbf{Absolute Exterior Angle Theorem} AXAT.
Of course, since we drew it in the Euclidean plane, we can also read off the
Euclidean Exterior Angle Theorem (EXAT) but we'll come to that in much later lessons.
\end{document}
Recall that $\angle BAC \cong \angle CB'' B'$ follows by SAS to prove that
$\triangle BAC \cong \triangle CB'' B'$. This is the \txtbf{Absolute Exterior Angle Theorem} AXAT.
Of course, since we drew it in the Euclidean plane, we can also read off the
Euclidean Exterior Angle Theorem (EXAT) but we'll come to that in much later lessons.
\end{document}