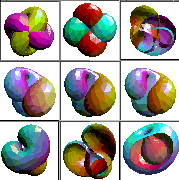Supercomputing'95 Information Architecture
GII Testbed for I-WAY Applications,
Entry #8
LATERNA matheMAGICA

Project Director:
George Francis,
Mathematics Department,
University of Illinois.
Faculty Collaborators:
Ken Brakke, Mathematics Department, Susquehanna University.
Rob Kusner, Mathematics Department, University of Massachusetts.
Dennis Roseman, Mathematics Department, University of Iowa.
John M Sullivan, Mathematics Department, University of Minnesota.
Student Collaborators:
Ulrike Axen,Computer Science Department, UIUC.
Alex Bourd,Mathematics Department, UIUC.
Glenn Chappell, Mathematics Department, UIUC.
Chris Hartman, Mathematics Department, UIUC.
Paul McCreary, Mathematics Department, UIUC.
Jason Rubenstein,
Electrical Engineering Department, UIUC.
Will Scullin, Computer Science Department, UIUC.
Why we're doing this.
With powerful parallel computers networked to virtual environments,
we can explore previously inaccessible problems in geometry, especially
where a complex object evolves so as to optimize its shape. For instance,
an unknotted loop of string, no matter how tangled, can be
persuaded to move (automatically and without breaking) into a round circle.
In 4-dimensions, a surface (like a topological sphere) may
be knotted. When it is merely tangled we evolve it to its familiar
round shape to show it was unknotted. We guide surfaces towards
optimality by minimizing mathematical abstractions of physical energies
like the Coulomb potential or the bending energy of bilipid membranes.
Mathematical surfaces in 3-dimensions (like shadows from 4-dimensions)
generally self-intersect, but the Willmore bending energy can still be
used to optimize their shape. A sphere can be turned inside out, keeping
the surface smooth, but allowing complex self-intersections; we demonstrate
this by presenting for the first time a geometrically optimal and
computationally automatic eversion of the sphere.
What we're showing you.
We present a play in four acts in the CAVE. Several unknots, evolving on
separate computers, untangle in a few seconds. The morphing of a rumpled
sphere in 4-space to a round sphere is made visible to us by slicing it
with our 3-space as the knife, and projecting it to our 3-space as a canvas.
A symmetrically interpenetrating sphere in 3-space, Morin's half-way model,
evolves down both sides of a saddle in its bending energy potential field.
As the triple points and double curves disappear, the invagination of
a gastrula pops out, and we see that the ordinary spheres at the ends of
the deforming homotopy are inside-out from each other.
Here are some pictures.
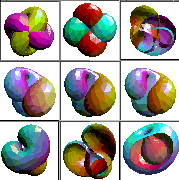

How we're doing it.
The principal tool for doing this is our powerShell, a tightly articulated
pair of model programs designed to be easily customized for any particular
application. One part of this pShell is a scalable, coarse-grained parallel
`calculator' distributed on shared-memory multi-processor computers, such
as a Power Challenge Cluster. The other is the `viewer' powering the CAVE
from an Onyx. Our calculator is Brakke's Surface Evolver, whose output is
translated to a format suitable for high-speed, broad-band transmission on
the Iway. The viewers are based on our highly successful illiShell
paradigm developed for the CAVEs at SIGGRAPH'94. Some of the software
used is available for downloading.
People who helped us.
Andrew Hanson, Computer Science Department, Indiana University.
Louis F. Kauffman, Mathematics Department, U. Illinois at Chicago.
Stuart Levy, The Geometry Center, University of Minnesota.
Tamara Munzner, Computer Science Department, Stanford University.
Mark Phillips, The Geometry Center, University of Minnesota.
Alan Verlo, The Electronic Visualization Lab, U. Illinois at Chicago.
The National Center for Supercomputing Applications
(NCSA),
UIUC.
The Electronic Visualization Laboratory
(EVL),
UIC.
The Center for Geometry, Analysis, Numerics and Graphics
(GANG),
UMass.
The Geometry Center, University of Minnesota.
NSF ASC-93-00042 at NCSA.
NSF DMS-94-04278 and DOE DE-FG02-86ER25015 at GANG.
Back to the grafiXlab.
Last edited 27jan96 gkf