- Home General Information
- Kepler's Laws The What, When, and Why of Planetary Motion
- The Project (Somewhat) Interactive Models of Each of the Laws
- Documents The Plan, Results, and Credit when Due

Kepler's Laws, Universal or Not?
By Jake Ribich
- - -Keplers Three Laws
While it may seem as though the heavens are an unorderly place, each and every planetary body actually follows the same set of patterns. These patterns were at one point only theory, but they now exist as universal laws. However, this project will focus exclusively on the planets within our solar system.The first law states that the orbit of a comet or planet is always conic in shape. Whether an ellipse, hyperbola, or parabola, each planetary motion can be modeled and predicted by the mathematics of each type of path. The second law exists as an extension of the first, but is dependent on the line segment connecting the planet to the sun. It states that this line segment sweeps over equal areas in equal periods of time. Finally, the third law only holds true for objects with closed, or elliptical, orbits. This final law relates the square of the orbital period to the cube of the semimajor axis of the orbit. Luckily for us, every planet within our solar system follows a closed orbit and we can therefore illustrate the third law with the same planetary bodies as will be used in the first two parts.
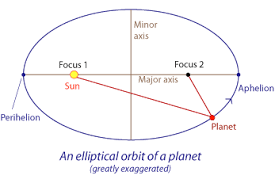
-The First Law
The orbit of every planet is an ellipse with the Sun at one of the two foci.
Kepler's first law does in fact hold true for every planetary body, but an elliptical orbit is actually a specific case. All orbits just have to be conic in some nature. This includes ellipses, hyperbolas, parabolas, and occasionally circles. In the case of our solar system, however, every orbit is an ellipse with the sun located at one of the foci. All this really means in that the planet will move faster when it is closer to the sun and slower when it is on the other side of its orbit.
 .
.
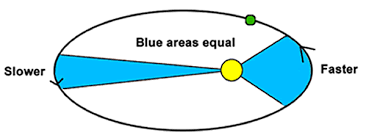
The Second Law
The line segment joining the sun to a planet sweeps out equal area in equal times.
This law describes the speed at which planets orbit the sun based on how far away from it they are at any given time. A planet moves fastest when it is closer to the sun and slowest when it is further. Even though the speeds of the planets are constantly changing, if a line was drawn from the center of the planet to the center of the sun, that line would sweep out the same area in the same amount of time no matter where it was. For example, if this line existed between the earth and the sun, then the area swept over by this line over the course of every thirty one day month would be the exact same.
 .
.
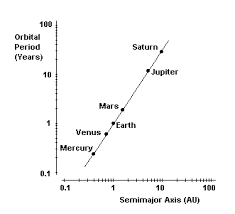
The Third Law
The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit.
The third law is a little different than the first two because it makes a comparison between the motions of multiple planets instead of just describing the motion of one planet. The comparison that is being made is that the ratio of the squares of the periods to the cubes of their average distances is the same for every planet. Amazingly, this ratio does not change no matter which planet you are looking at and can help to accurately describe the period and distance of a planets orbit around the sun.
 .
.
-
