Geometry

Historical Transmission

After the late 8th century, Euclid's The Elements were translated into Arabic through the House of Wisdom in Baghdad. There are many Arabic editions of and commentaries on The Elements, which shows the influence Euclid had on Islamic mathematics, and especially on Islamic geometry (Berggren 1986, 72). Muslim mathematicians also had a great respect for Archimedes' On the Sphere and Cylinder. In his preface, Archimedes mentions his discovery of the area of a segment of a parabola; since his treatise on this particular subject was not translated into Arabic, Thābit ibn Qurra and his grandson Ibrāhīm ibn Sinān searched (with great success) for a proof of Archimedes' result. Thābit ibn Qurra actually translated or revised translations of all of the Archimedean works existing in medieval Arabic, including the text The Heptagon in the Circle, which Arabic sources attribute to Archimedes but does not exist in Greek (Berggren 1986, 72).

Another important work in Islamic geometry was Apollonios of Perga's The Conics from about 200 BC. Though The Conics contained eight chapters or books, only four exist in Greek and only seven in Arabic. These three Greek scholars -- Euclid, Archimedes, and Apollonios -- formed the basis of Islamic mathematics. Muslim mathematicians and translators are responsible for the preservation and transmission of these texts through the medieval period.

Geometrical Developments

Abū Sahl Wayjan ibn Rustam al-Qūhī

Abū Sahl lived around 940-1000 CE. He was from Kūh, a mountainous area along the southern coast of the Caspian Sea in modern Iran. (Kūh is the Persian word for mountain.) Abū Sahl worked in the Baghdad and is considered one of the greatest Muslim geometers in the 10th century. Though Abū Sahl worked on many treatises on geometry and astrology, his explanation of the construction of a regular heptagon best shows his innovation as a geometer and his contribution to Islamic mathematics by providing solutions to "impossible" problems within known mathematical theories (Berggren 1986, 77).

Archimedes' construction of the regular heptagon was unexplained and unique in Greek mathematics, and so served more as a proof of the existence of a regular heptagon than a construction of it (Berggren 1986, 78). Abū Sahl analyzed the problem backwards, considering an already constructed heptagon and reasoning backwards. If his chain of reasoning can be reversed, then Abū Sahl has the proof of what is required starting from a given to the finished heptagon. His analysis was provided in a treatise dedicated to King `Adud al-Daula, the Buwayhid ruler of modern-day Iraq and Iran under the Abassid caliph Al-Muti. Abū Sahl's result showed that constructions which did not fit into any theories could be fitted into the theory of conic sections, a new development in geometrical thought. He first reduced the problem from a heptagon to a triangle, then from the triangle to the division of a line segment, and finally from the divided line segment to conic sections. Putting these steps back together, then, Abū Sahl proves (begining with conic sections) that a regular heptagon can be constructed and exists.

Ibrāhīm ibn Sinān ibn Thābit ibn Qurra

Ibrāhīm ibn Sinān (d. 946) is the grandson of Thābit ibn Qurra, the famous mathematician and translator of Archimedes. His treatment of the area of a segment of a parabola is the "simplest that has come down to us from the period prior to the Renaissance" (Berggren 1986, 87). He wrote that he invented the proof out of necessity, to save his family's scientific reputation after hearing accusations that his grandfather's method was "too long-winded" (Berggren 1986, 87). He also was concerned with methods and theories over particular problems, as seen in his treatise On the Method of Analysis and Synthesis in Geometrical Problems. His work On Drawing the Three Conic Sections is a discussion, with proofs, of how to draw the parabola and ellipse. He also gave three methods for drawing the hyperbola, which may be because of the interest in the hyperbola by instrument-makers.

Abū Nasr al-Farabi

One of the most impressive parts of Islamic culture has always been the elaborate geometrical artwork showcased in wood, tile, paintings, and mosaics. As geometers recognized this tradition, as well as the geometrical problems artists solved, they began to "justify the procedures and to see how far various methods could be pushed" (Berggren 1986, 89). The eighth book of Pappos of Alexandria's Mathematical Collection deals with instruments and machines of craft artisans, and includes an interesting section on geometrical constructions that can be created with only a straightedge and a compass with one fixed opening, sometimes referred to as a "rusty compass" (Berggren 1986, 89-90). This text, and especially the eighth book, was translated into Arabic and copied numerous times, pointing to its wide influence in the Islamic empire.

One text on geometrical constructions is one by Abū Nasr al-Farabi (870-950 CE). He taught philosophy in both Baghdad and Apello (in northern Syria), and was killed by highway robbers outside Damascus in 950 CE. He wrote a treatise called A Book of Spiritual Crafts and Natural Secrets in the Details of Geometrical Figures, which was later incorporated into Abu'l-Wafa's work On Those Parts of Geometry Needed by Craftsmen. Translations of two problems from this treatise are shown here, taken from the excerpts provided in (Berggren 1986, 90-2).

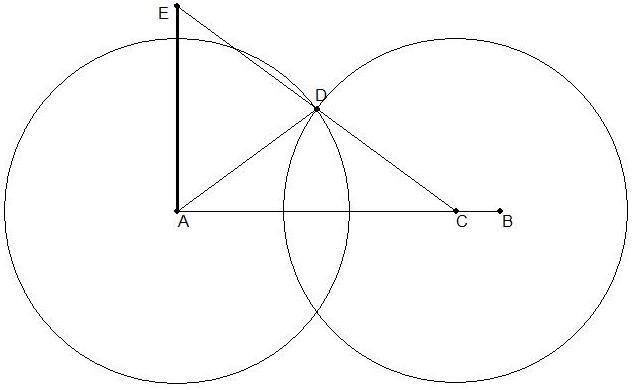
"To construct at the endpoint A of a segment AB a perpendicular to that segment, without prolonging the segment beyond A.

Procedure. On AB mark off with the compass segment AC, and, with the same opening, draw circles centered at A and C, which meet at D. Extend CD beyond D to E so that ED = DC. Then angle CAE is a right angle.

Proof. The circle that passes through E, A, C has D as a center since DC = DA = DE. Thus EC is a diameter of that circle and therefore angle EAC is an angle in a semicircle and hence is a right angle" (Berggren 1986, 92). (See the figure below.)

"To divide a line segment into any number of equal parts [-- for example, three equal parts].

Procedure. Let it be required to divide the line segment AB into the [three] equal parts AG = GD = DB. At both endpoints erect perpendiculars AE, BZ in different directions and on them measure off equal segments AH = HE = BT = TZ. Join H to Z and E to T by straight lines which cut AB at G, D respectively. Then AG = GD = DB.

Proof. Indeed, AHG and BTD are two right triangles with equal angles at G and D (and therefore at H and T). In addition HA = BT. Thus the triangles are congruent and so AG = BD. Also the parallelism of HG and ED implies that the two triangles AHG and AED are similar, and thus DG/GA = EH/HA. But, EH = HA and so DG = GA" (Berggren 1986, 92-3). This proof by similarity is obvious from the picture below. (See figure below.)

Please see the "Paper" section for further information on geometric contributions of Muslim mathematicians.