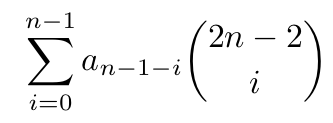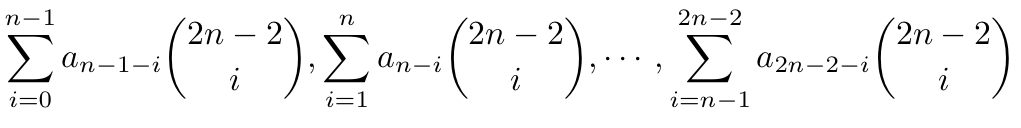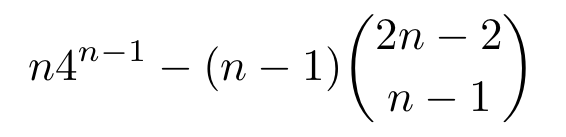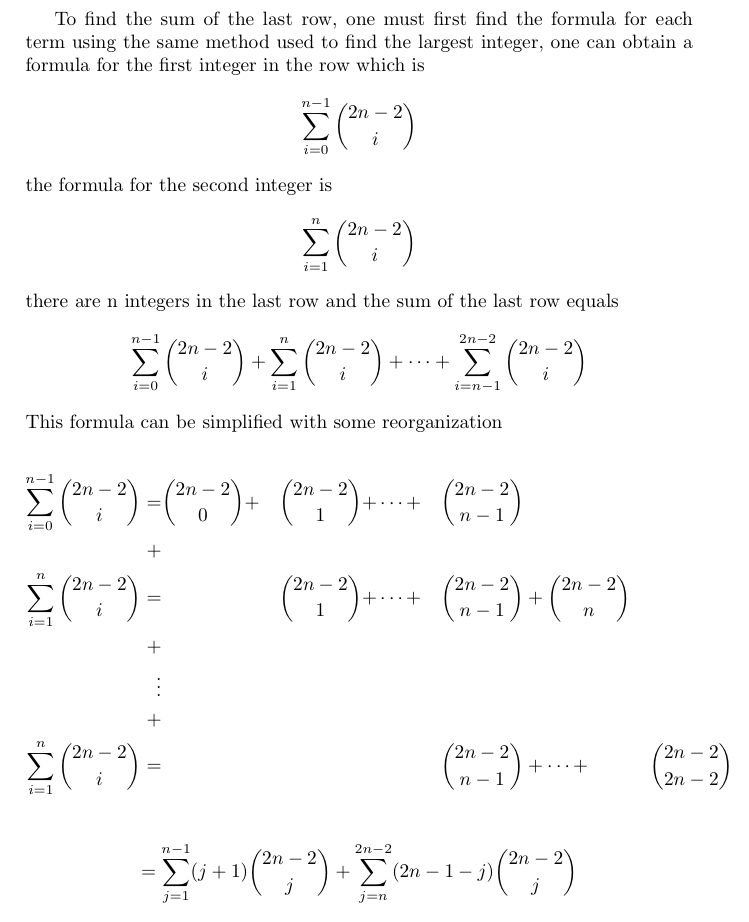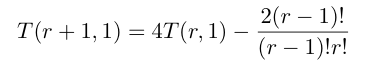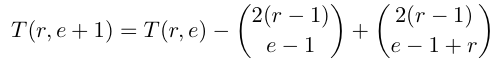Lisa Hickok

This is a website available at http://new.math.uiuc.edu/illimath/lhicko289/pres.html

This presentation is based on a paper I wrote. paper

Specials thanks to Professor Bruce Reznick, a Professor of Mathematics at the University of Illinois at Urbana-Champaign. He was my professor for Math 498, and he mentored me through this project.

All graphs were generated using Mathematica.

Here are the notebooks I used.

An Interesting Problem

hexvar.png

Given a hexagon with an arbitrary first row, What will be the value of the largest entry?

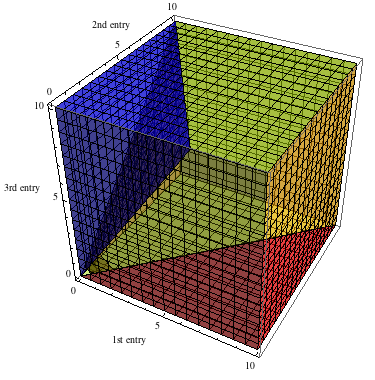
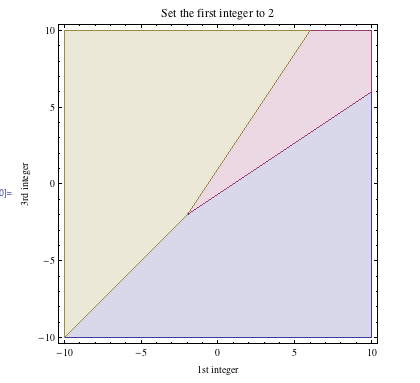
This is a graph I made to help solve the problem:

hexgraph1.png

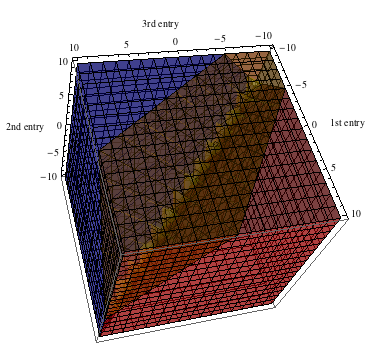
However the entries can also be negative

hexgraph2.png

The red region is where the 1st number in the last row is the largest.

The yellow region is where the 2nd number in the last row is the largest.

The blue region is where the 3rd number in the last row is the largest.

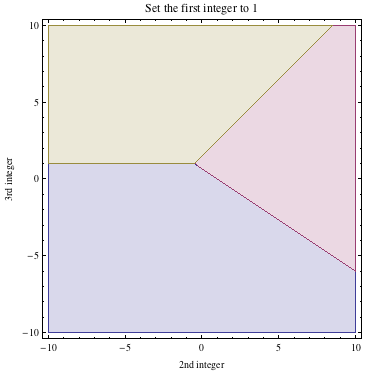
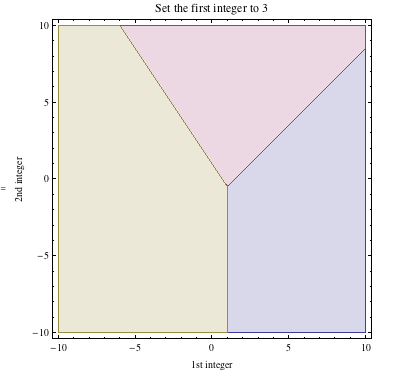
Here are some 2D graphs The purple region shows when the 1st integer of the last row is the largest. The red region shows when the 2nd integer of the last row is the largest. The yellow region shows when the 3nd integer of the last row is the largest.

hexgraph3.png hexgraph4.png hexgraph5.png

Here are some rules of thumb: If all the numbers in the first row are positive and the middle term is the largest, then the middle term in the last row is the largest. If the first or last number is the largest than the corresponding number in the last row is the largest if the difference between it and the center number is greater than 3/2 the other number.

General Case

The question really has two parts:

What is a hexagon and how is on constructed?

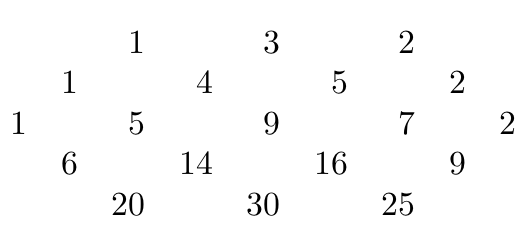
A hexagon is constructed similar to a Pascal's Triangle, however the first row can consists of multiple integers instead of one.

            1       1       1
         1      2       2       1
     \ 1    3       4       3       1/
   (1) \ 4      7       7       4  /  (1)
(1)   (5)\  11      14      11   / (5)   (1)

To construct a hexagon with side length n, either:

Specific Case

Before dealing with the general case, I focused on the case where the first row is made entirely of 1's

Examples

examples.png

The Largest Number

In this case the largest number will always be the entry in the center of the last row. This solves the problem of determining which entry in the last row is the largest but we need a formula for that entry.

To find the formula for that we will need the following theorem:

thm1.png

Using this theorem, we are able to find the formula for the largest number thm2.png

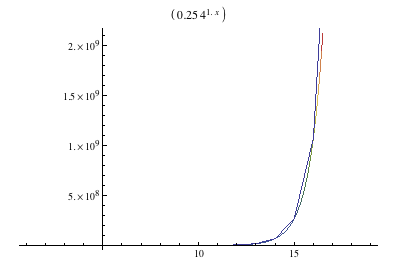
I found a formula but I was unable to find a recursion or a pattern for the sequence of the largest numbers. However, the numbers appear increase by a factor of four.

graph.png

The graph shows that the function of the largest numbers is approximated by the function `y =.25*4_^x`.

Back to the General Case

Let the first row be a_0, …, a_n Using what I learned from the case above I found the formula for the first number in the last row

form1.png

And then the last row is equal to:

form2.png

Second Question

I also wanted to a find a formula for the last row of a Hexagon.

If the first row consists on n 1's then the formula for the sum is

thm3.png

The following is the proof:

thm4.png thm5.png thm6.png

Another Triangle

From the hexagons I constructed another triangle tri.png

The rows of the triangle are the last rows of the hexagons. I have developed formulas so the triangle is self generating.

Entry = T(row number, entry number)

triform1.png

triform2.png

Future Work

tri3d.png hex3d.png

I did find a formula for the largest number in the 3D space `sum (2*n)! /(((i+j)!)*((j+k)!)*((k+i)!))` where `n=i+j+k`, `0<=i<=n` ,`0<=j<=n`, `0<=k<=n`