Read a few papers about the LBM, HPP, and FHP CA.
A list differences between Lattice Boltzmann Methods (LBM) and regular numerical methods are found in Chen and Dollen’s paper. The differences include:
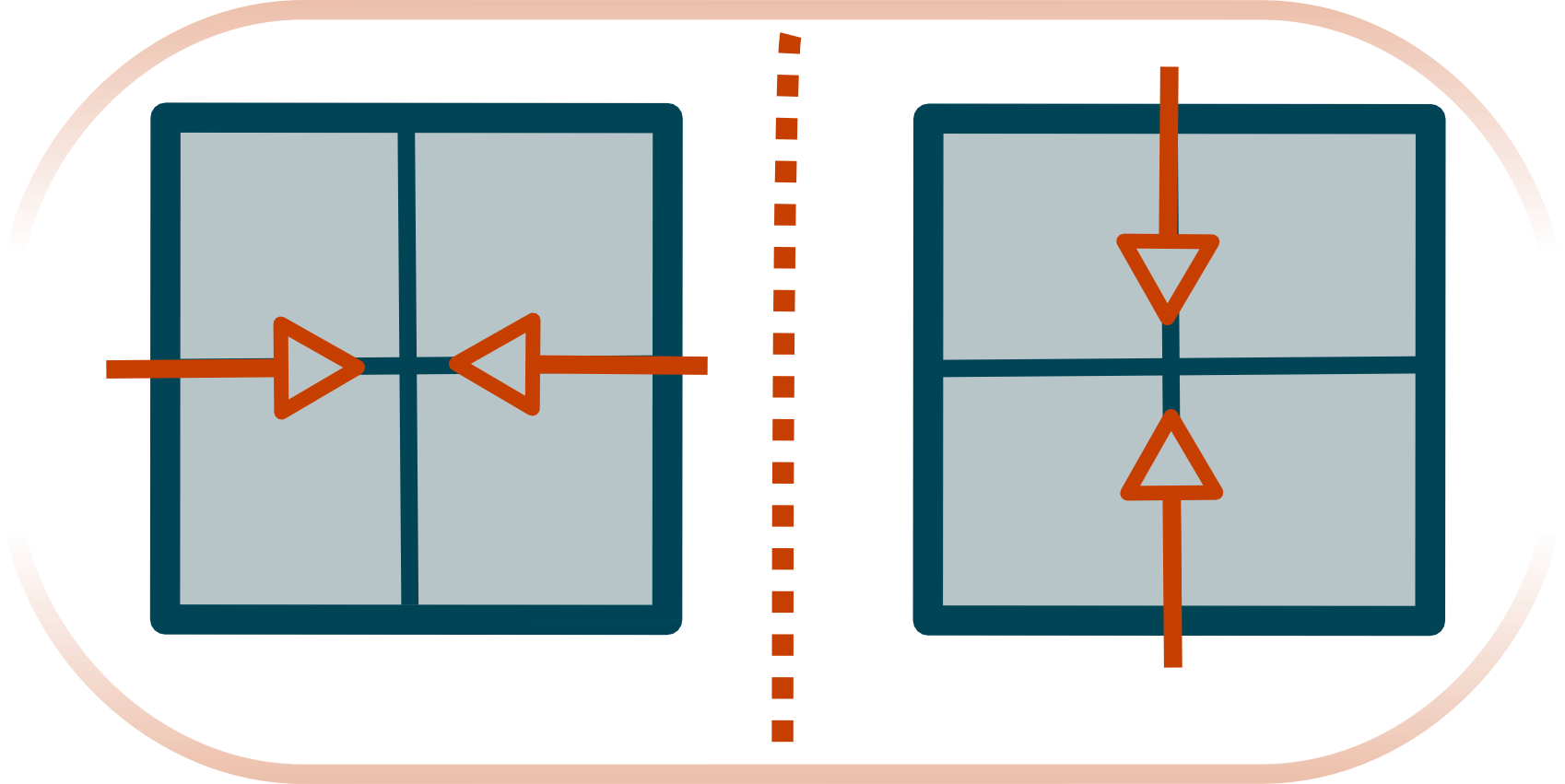
One of the first attempts to use CA to approximate NSE is called the HPP model after “Hardy-Pomeau-Pazzis”, the authors of a 1973 paper describing the model. The idea of the model is quite simple:
The image bellow summarizes the gist of the model

While such a model is simple and ideal for 1973 (when parallel computing was the fad), if we consider its limit, it does not approximate the NSE. This is partly because the inadequate rotational symmetry of the square lattice (having only $\pi/2$ symmetry).
The HPP model is still used to simulate sand mixed with water and other rigid liquids (need to find paper that mentioned this).
In 1986 it was realized that the only two dimensional lattice that remotely approximates the NSE was the hexagonal lattice. This model was realized by Frish-Hasslacher-Pomeau and a few months later independently by Wolfram (who references the 1986 article in CA fluids 1). The model was extended to 3 space by FHP in 1987.
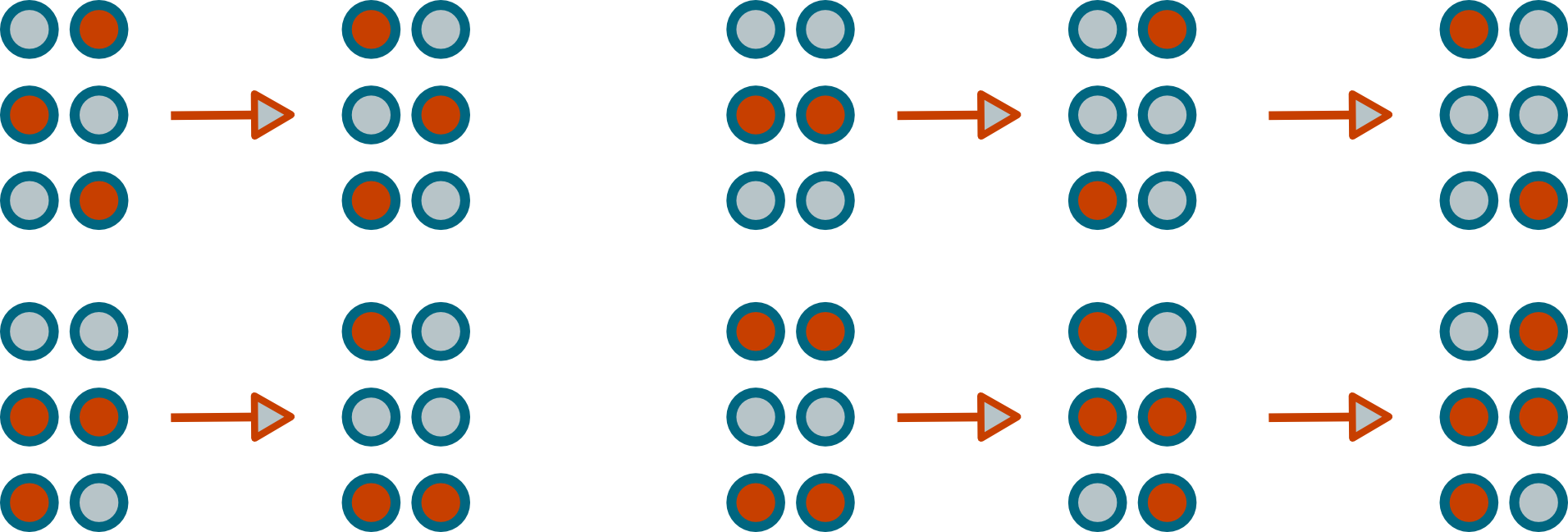
The FHP model is similar to the HPP model. Again, only one particle can be at any position on the grid. The update rules are a bit more complex, and described by the following figure (appears in "Lattice-gas cellular automata and lattice Boltzmann by Dieter (springer) and page 378 in NKS).
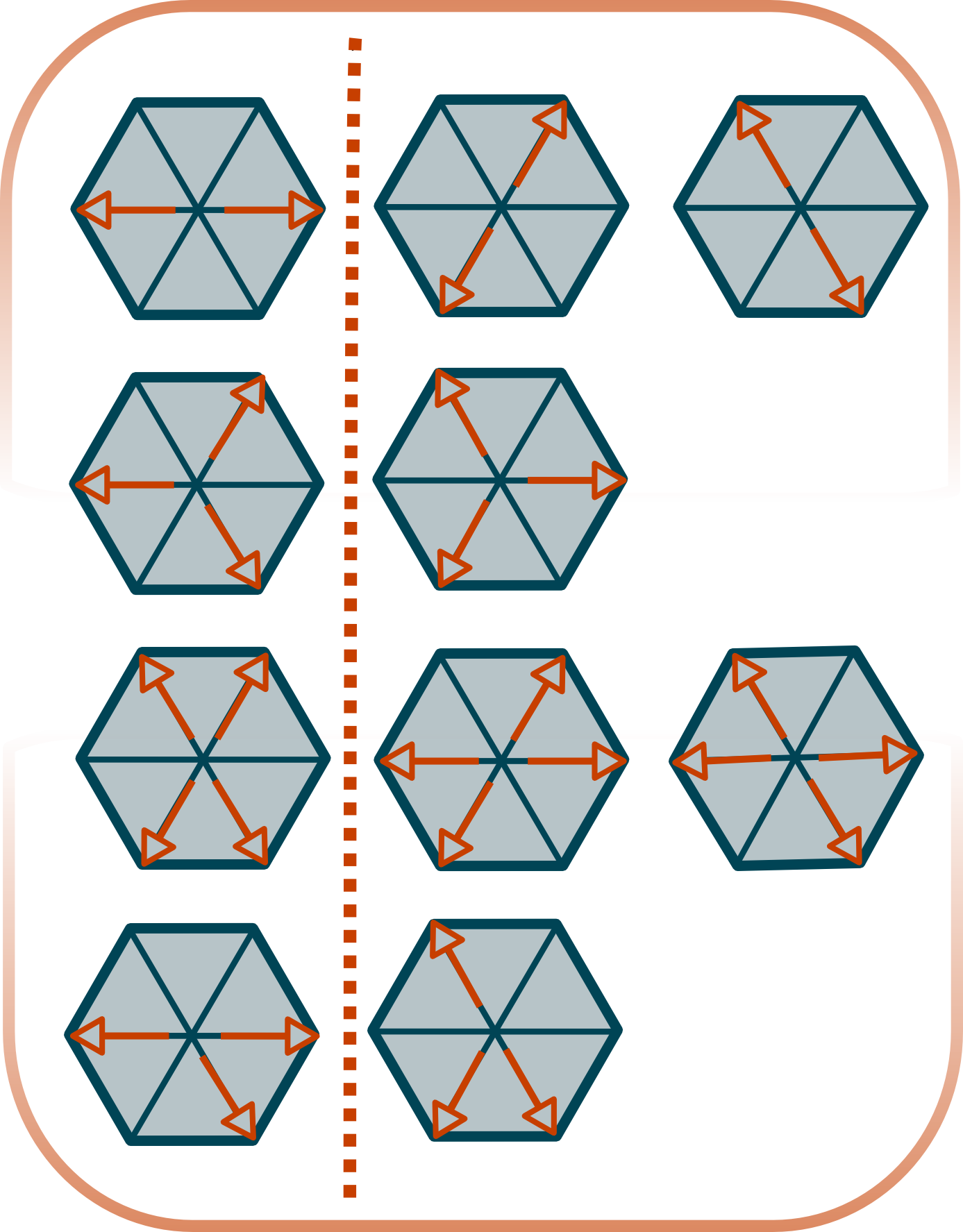
An output is selected randomly if multiple outputs can be realized.
My first attempt to implement the FHP CA did not go anywhere because I had no idea how to generate the hexagonal lattice. Most of the time was thus devoted figuring out the optimal way to generate and represent the lattice.
While the CA is simple, I wanted to look at how to optimize my grid code as early as possible, since it would be a bottle neck if the lattice is scarce.
The first question was how to represent that lattice as an array. A Naive was is to think of the two dimensional array in terms of $3 \times 3$ blocks. Each of these blocks represents a single lattice; shown bellow.
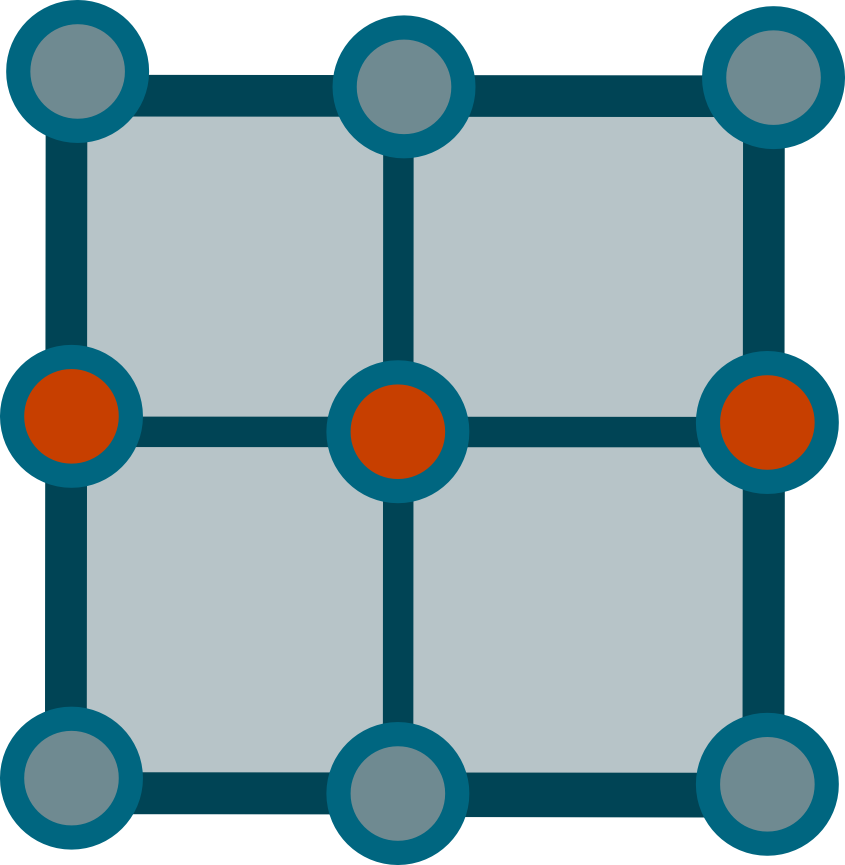
It should be easy, however, to see that such representation would waste 3 positions that the model does not care about. An alternative approach is to remove the middle row from the representation, and concentrate on the first and last row. We thus get the following representation
6 1
5 2
4 3
based on the following numbering scheme
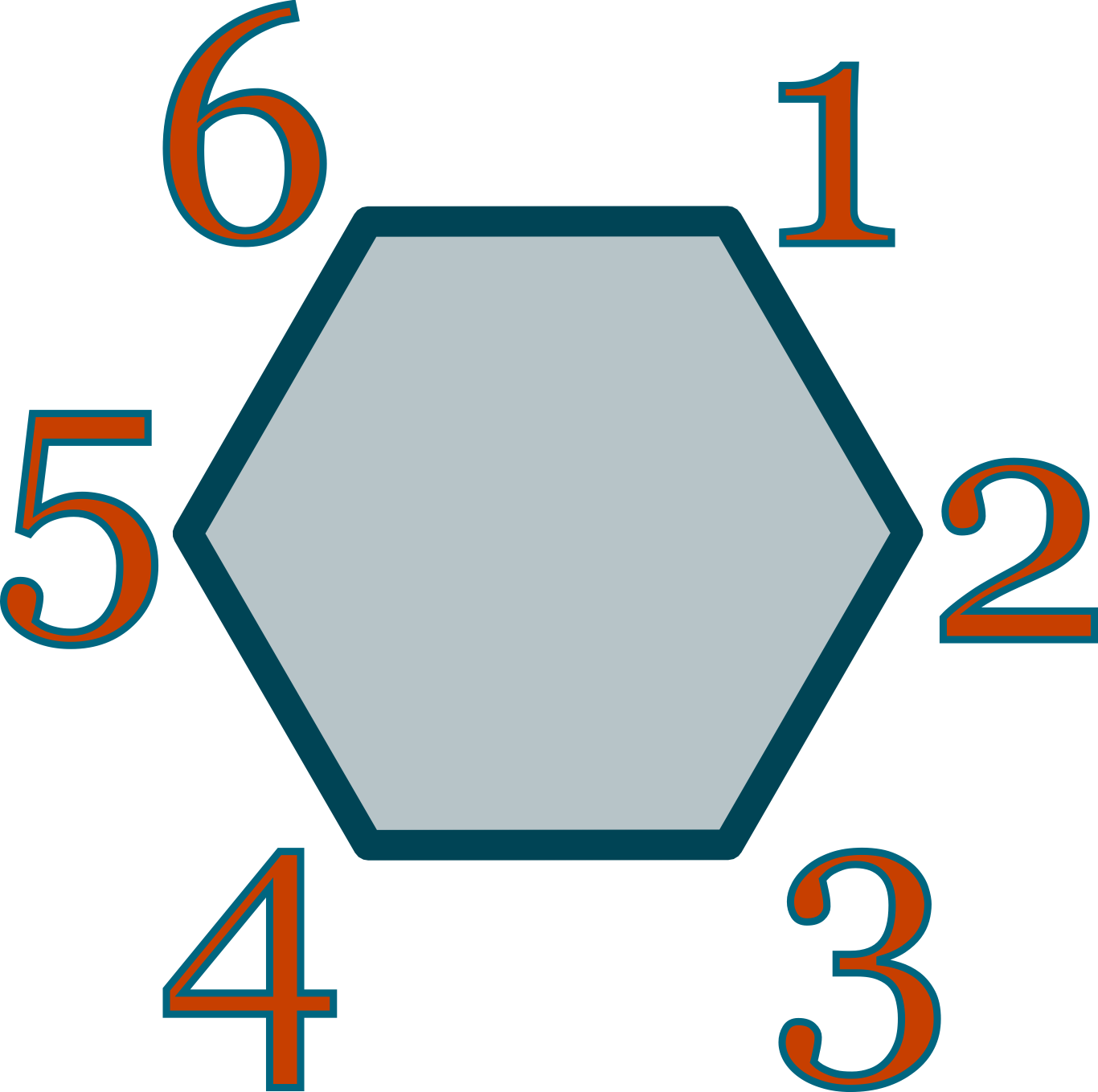
A $3 \times 2$ block. If we then rewrite our representation in of the FHP model using this representation we get
It should be noted that if we want $n^2$ lattices ($n$ rows with $n$ columns) then we do not need a $n*3 \times n*2$ array. This can is evident if we stack more lattices in this representation.
6 1
51 26
462 351
531 462
426 5131
35 42
4 3
Which represents the orange region found in the following pictorial representation
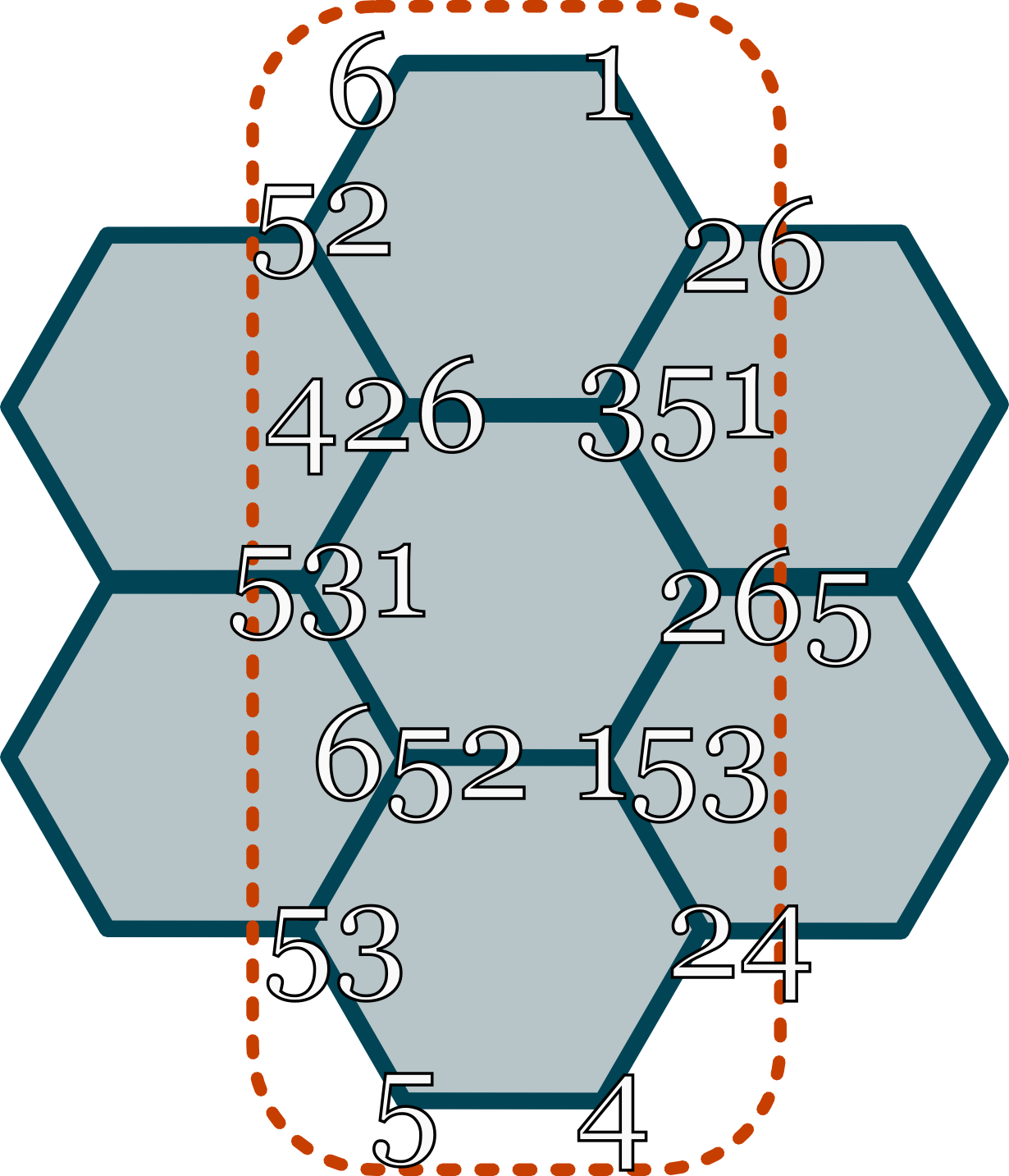
This $7 \times 2$ represents on three lattice rows with one lattice per row. We can generalize the size of the matrix to be
2*num_of_lattice_rows + 1 x num_of_lattice_columns + 1
Note: Originally I was representing this as a $2 \times 3$ matrix
6 1 2 5 4 3because of some complications writing this section, however, I chose to switch to a $3 \times 2$ coding scheme.
Revised the representation of the lattice. Started coding the FHP model.
After talking to Dr. Francis who explained some the history behind I was doing, I decided to go back and implement the simpler HPP model in Python, in the end, however, it did not work.
One question that I and Dr. Francis had was what exactly did Wolfram try on the Connection Machine. After a few hours of research, I found some interesting information. The following is a snippet of an email exchange between me and Dr. Francis on the topic.
This <
http://www.stephenwolfram.com/publications/articles/ca/88-cellular/1/text.html>
is about the only time wolfram mentions his work on the connection machine
in the 1980s. As to what type of method he used, one has to look elsewhere
from < http://www.longnow.org/views/essays/articles/ArtFeynman.php >
" Cellular automata started getting attention at Thinking Machines when
Stephen Wolfram, who was also spending time at the company, suggested that
we should use such automata not as a model of physics, but as a practical
method of simulating physical systems. Specifically, we could use one
processor to simulate each cell and rules that were chosen to model
something useful, like fluid dynamics. For two-dimensional problems there
was a neat solution to the anisotropy problem since [Frisch, Hasslacher,
Pomeau] had shown that a hexagonal lattice with a simple set of rules
produced isotropic behavior at the macro scale. Wolfram used this method on
the Connection Machine to produce a beautiful movie of a turbulent fluid
flow in two dimensions. Watching the movie got all of us, especially
Feynman, excited about physical simulation. We all started planning
additions to the hardware, such as support of floating point arithmetic that
would make it possible for us to perform and display a variety of
simulations in real time."
The above quote comes partly from a book called "Feynman and Computation,"
and that is the only reference to CA and fluids (or wolfram) in that book. A
more (auto)bibliographical account can be found in NKS <
http://www.wolframscience.com/nksonline/page-880b-text >
"I had always thought that cellular automata could be a way to get at
foundational questions in thermodynamics and hydrodynamics. And in mid-1985,
partly in an attempt to find uses for the Connection Machine, I devised a
practical scheme for doing fluid mechanics with cellular automata (see page
378 <http://www.wolframscience.com/nksonline/page-378-text>). Then over the
course of that winter and the following spring I analyzed the scheme and
worked out its correspondence to the traditional continuum approach.
By 1986, however, I felt that I had answered at least the first round of
obvious questions about cellular automata, and it increasingly seemed that
it would not be easier to go further with the computational tools available.
In June 1986 I organized one last conference on cellular automata--then in
August 1986 essentially left the field to begin the development of *
Mathematica*."
He thus used the FHP model that I am trying to get to work right now. Also,
the 4D fluid simulation is called FHCP <
http://arxiv.org/abs/chao-dyn/9508001v1 >
It should also be mentioned that Wolfram patented not only the hexagonal
method for solving fluid dynamics, but the entire lattice gas method as a
whole. See patent number 4809202 <
http://www.google.com/patents?id=FF4WAAAAEBAJ&dq=U.S.+Patent+Number+4,809,202>
I realized that my interpretation of the model was incorrect the entire time. After I gave a presentation, received some helpful tips, and learned more, I decided to start from scratch. After a few hours, I was able to correctly implement the HPP model. The implementation, along with the algorithm, is detailed in HPP document posted on the website.
Looked at how Jared Schaber, and wrote notes. Talked to Jonathan Manton who described how to implement the FHP model (I wish I had that talk before, since I figured out much of what he said the day before). Jonathan also explained the concepts behind CUDA, compiler optimization, and a slew of other things. He also gave me tips on how to optimize my program, while stressing that clarity is the most important objective at the beginning.
In Cellular Automata Super Computers for Fluid Dynamics Modeling (by Margolus) the author writes the following about implementing CA in conventional architecture (not CAM):
two dimensional planes are processed serially (with a substantial amount of pipelining); a third dimension is achieved by staking planes and operating on them in parallel.
The question is: how can this be achieved without running into race conditions.