Measure a Box Exercise

In this exercise we shall simulate the determination of the perspective frame from a given box in perspective. This can be done either "by hand", that is, with a transparent right triangle ruler (a gnomon) on paper, or in KSEG. We shall distinguish between these two methods only when there is a significant difference.

Recall that we abbreviate by $ (AB) $ the infinite line $ \ell_{AB} $ through the two points. Sometimes we need to distinguish between the segment or edge $ e_{AB} $ between the points, the ray $ \r_{AB} $ from $ A $ through $ B $, and the translation $ \tau_D $ determined by the displacement vector $ D = B-A $. When ambiguity threatens, we’ll use email notation, written in the order that KSEG prefers:

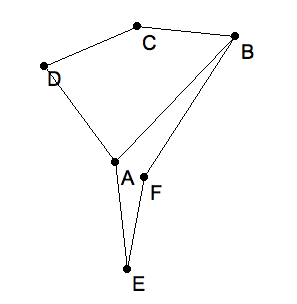
Given six points that form a convex quadrilateral $ ABCD $ and a second quadrilateral $ BAFE $. Please do not move the first five points except small distances to avoid undesirable coinidences.

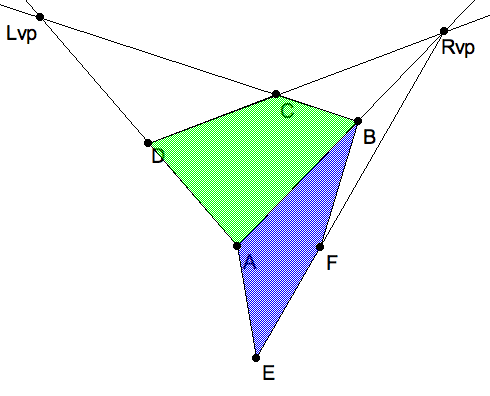
As we saw in the very first drawing exercise in perspective, the convex quadrilateral $ ABCD $ may be regarded as a a square in perspective from some point in space. Here we proceed only from the assumption that $ ABCD $ represents a planar rectangle drawn in perspective. In that case we can determine the left and right vanishing points $ Lvp, Rvp $ for the parallel sides of the rectangle, and the line $ h=(LR) $ which is the horizon for the plane the rectangle lies in.

We further assume the vertical near edge $ AE $ of the box, is given, but that vertex $ F $ is "in the wrong place." To test that you understand the role of vanishing points, move $ F $ to its correct place. Here is a hint. Since all three edges $ DC, AB, EF $ are parallel in reality, $ F $ must be on $ ERvp $. It is therefore wise to delete the initial choice of $ F $ and choose an $ F $ on $ ER $.

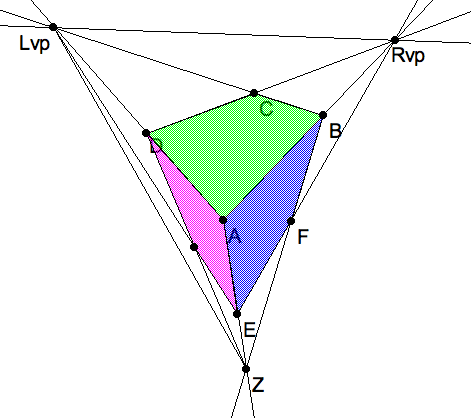
This choice determines the third vanishing point $ Z $ where both parallel lines $ AE $ and $ BF $ vanish. Now complete the box in perpective by making sure the remaining two visible edges (and 3 addition hidden edge, if you need a transparent figure) vanish at the correct vanishing points. In an a priori perspective box, this will already be the case.

We shall assume that the three vanishing points $ R,L,Z $ are all in the picture plane. Then the $ \triangle RLZ $ determines the rest of the construction as follows. Recall that the 3 altitudes of $ \triangle RLZ $, which meet at the orthocenter, extend past their bases to the corners of the 3 Thales triangles.

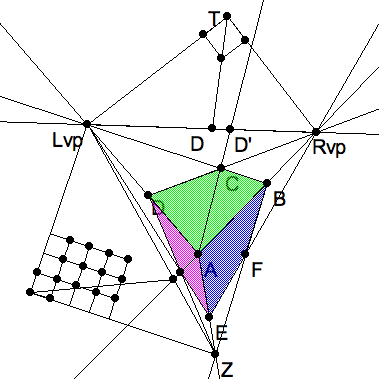
To find the corners of a Thales triangle, say $ \triangle RLT $ on the horizon, with in a hand drawing, first use your gnomon to drop a perpendicular from $ Z $ to $ h $. Extend this altitude above the horizon. Now slide you gnomon with its right angle on the extended altitude until its sides pass through the 2 vanishing points simultaneously. With KSEG it is useful to just apply the thales3pts.sec construction. You may have to reduce the size of the little square by pushing a free point on it towards $ T $. We shall call this little square the Thales tile to avoid confusing it with any other squares in the perspective picture. Recall that the Thales figure is in the Euclidean plane and the rules of Euclidean geometry apply.

Shooting the diagonal $ AC $ of the top face of the perspective box to the horizon, $ D' = (AC)(RL) $, will generally not be at the diagonal point unless the top face happened to be square in reality. A way to measure the proportions of the top face is to reconstruct the orthographic rectangle in the Thales corner whose diagonal is $ TD'$.

For this purpose, it is convenient to extend the Thales tile in the Thales corner to a square grid. By hand you’ll need a compass to measure off edge lengths and consgtuct right angles. But you can use a strip of paper to copy lenghts, and your gnomon to approximate right angles. With KSEG choose one edge of tile as a translation vector, and chose the angle (vertex and adjacent edges) of the tile opposite $ T $ to translate a number of times. Then do the same in the opposite direction.

Since the Thales triangle and its tiled grid lies in the Euclidean plane, you could also measure lengths in some units, and take their ratio. But that is less artistic.

Do this for one of the side faces, called elevations, to obtain a second ratio. Now use our high school algebra skills, figure out the proportion $ a:b:c $ of the three dimensions of the box. For example, if one face measures out to have porportion $ a:b $ and the other has proportion $ b':c' $ with $ b, b' $ corresponding to the common edge, then $ c = \frac{b}{b'} c' $.

If the initial box is in 2 point perspective, so that $ Z $ is ideal, then it is still possible to measure the height. Although there is no orthocenter to the ideal triangle, the eye center is on the horizon. The Thales tile for a vertical face of the box sits in the Thales corner on the horizon. Use it to tile a square grid as before to estimate the proportions, or measure in some convenient metric units.