Exercise on Perspective Squares
28jun10\begin{document} \maketitle
 \secton{Introduction}
It is surprising that every convex quadrilateral $ABCD$ in a
painter's canvas is a square in perspective from at least one
position of the painter's eye relative to the canvas. The problem
to be solved here is to locate such viewpoints.
\subsection{Using KSEG}
Renaissance painters, who invented perspective, obviously didn't
have a computer drawing program. They use rule and compass. So
the following recipe is equally valid for ruler and compass as it
is in KSEG. But for this assignment, you submit one .seg file with
the solution.
\section{Exercise}
Choose four initial points in the plane representing the painter's
canvas. Be sure they form a convex quadrilateral. Let the vertices
be $ABCD$ in counterclockwise order.
Next, construct the horizon line $ h = ((AB)(CD))((BC)(DA)) $.
You may need to wiggle the given points so that the two
vanishing points $(AB)(CD)$ and $(BC)(DA)$ are in the visible part
of your canvas. If you rotate the quadrilateral, you can get
$h$ to be really horizontal, and these two vanishing points to be
the $LVP$ and the $RVP$ as in the notes.
This much alone establishes your quadrilateral to be a rectangle
in perspective from every viewpoint. Why is that?
You need to understand the theory of lesson P3 to follow the
next construction.
On the horizon, construct a semicircle with diameter the segment
between the left and right vanishing points of the rectangle in
perspective. One of the two diagonals of the quadrilateral,
when extended, crosses the horizon at the diagonal vanishing point,
$DVP$. In the semicircle it is necessary to construct a Thales
triangle so that the bisector of the right angle crosses the
horizon at the $DVP$. But how to do that?
One solution is trial and error. Construct any Thales triangle,
bisect the right angle at $T$, and wiggle $T$ along the semicircle until
the construction is correct. This will lead to a correct picture,
but not to a correct solution. Why not?
With ruler and compass, once you have drawn something, you can't
change it. With KSEG you can. We call this the "wiggle test".
Your construction must persist under changing the initial conditions.
So I will now give you the construction that works. In a subsequent
lesson (P6) you'll find out why.
\subsection{Hint on locating the Thales triangle}
Instead of a semicircle, draw the entire circle. Drop a radius
perpendicular to the diameter to the point at the very bottom of the
circle. Call it $S$ for "south pole". Next, draw $(SD)$ through $S$
and the diagonal vanishing point. Where $(SD)$ crosses the upper
semicircle, $T$, is where to put the right angle of the Thales triangle.
Verify this experimentally by showing that $(SD)$ really does bisect
the right angle at $T$.
Finally, by our theory, the eye-points in the canvas lies along the
altitude of the Thales' triangle you have constructed, but still
inside the circle with diameter from the left to the right vanishing point.
\section{Extra Credit Exercise on finding the focal distance.}
What remains to be determined is just how far the painter's eye must
be away from the canvas. This is the focal distance. For this you
need to understand the Horizon-Zenith construction.
\subsection{Hint}
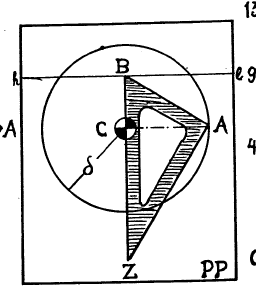
Look at the figure above. It is a detail from a figure in the lesson.
In it you see the horizon line, the eyepoint, called $C$ here. You
do not see the Thales triangle itself. But the point $B$ is the base
of the altitude of your Thales' triangle. And the distance from $B$
to $A$ in the picture is the length of the altitude. Therefore,
the focal distance is represented by the segment from $A$ to $C$.
To understand why this must be true requires some serious spatial
imagination, and I do not require you to supply it on this first
exercise. A labelled .seg file what holds together under wiggling
is suffcient.
\end{document}
\secton{Introduction}
It is surprising that every convex quadrilateral $ABCD$ in a
painter's canvas is a square in perspective from at least one
position of the painter's eye relative to the canvas. The problem
to be solved here is to locate such viewpoints.
\subsection{Using KSEG}
Renaissance painters, who invented perspective, obviously didn't
have a computer drawing program. They use rule and compass. So
the following recipe is equally valid for ruler and compass as it
is in KSEG. But for this assignment, you submit one .seg file with
the solution.
\section{Exercise}
Choose four initial points in the plane representing the painter's
canvas. Be sure they form a convex quadrilateral. Let the vertices
be $ABCD$ in counterclockwise order.
Next, construct the horizon line $ h = ((AB)(CD))((BC)(DA)) $.
You may need to wiggle the given points so that the two
vanishing points $(AB)(CD)$ and $(BC)(DA)$ are in the visible part
of your canvas. If you rotate the quadrilateral, you can get
$h$ to be really horizontal, and these two vanishing points to be
the $LVP$ and the $RVP$ as in the notes.
This much alone establishes your quadrilateral to be a rectangle
in perspective from every viewpoint. Why is that?
You need to understand the theory of lesson P3 to follow the
next construction.
On the horizon, construct a semicircle with diameter the segment
between the left and right vanishing points of the rectangle in
perspective. One of the two diagonals of the quadrilateral,
when extended, crosses the horizon at the diagonal vanishing point,
$DVP$. In the semicircle it is necessary to construct a Thales
triangle so that the bisector of the right angle crosses the
horizon at the $DVP$. But how to do that?
One solution is trial and error. Construct any Thales triangle,
bisect the right angle at $T$, and wiggle $T$ along the semicircle until
the construction is correct. This will lead to a correct picture,
but not to a correct solution. Why not?
With ruler and compass, once you have drawn something, you can't
change it. With KSEG you can. We call this the "wiggle test".
Your construction must persist under changing the initial conditions.
So I will now give you the construction that works. In a subsequent
lesson (P6) you'll find out why.
\subsection{Hint on locating the Thales triangle}
Instead of a semicircle, draw the entire circle. Drop a radius
perpendicular to the diameter to the point at the very bottom of the
circle. Call it $S$ for "south pole". Next, draw $(SD)$ through $S$
and the diagonal vanishing point. Where $(SD)$ crosses the upper
semicircle, $T$, is where to put the right angle of the Thales triangle.
Verify this experimentally by showing that $(SD)$ really does bisect
the right angle at $T$.
Finally, by our theory, the eye-points in the canvas lies along the
altitude of the Thales' triangle you have constructed, but still
inside the circle with diameter from the left to the right vanishing point.
\section{Extra Credit Exercise on finding the focal distance.}
What remains to be determined is just how far the painter's eye must
be away from the canvas. This is the focal distance. For this you
need to understand the Horizon-Zenith construction.
\subsection{Hint}
Look at the figure above. It is a detail from a figure in the lesson.
In it you see the horizon line, the eyepoint, called $C$ here. You
do not see the Thales triangle itself. But the point $B$ is the base
of the altitude of your Thales' triangle. And the distance from $B$
to $A$ in the picture is the length of the altitude. Therefore,
the focal distance is represented by the segment from $A$ to $C$.
To understand why this must be true requires some serious spatial
imagination, and I do not require you to supply it on this first
exercise. A labelled .seg file what holds together under wiggling
is suffcient.
\end{document}