Exercise on Completing a Cube, given an Edge.
28jun10\begin{document} \maketitle
 \section{Introduction}
This exercise is nothing more than actually carrying out the recipe for
drawing a cube in perspective, given one edge (and a 3-pt perspective
frame), as in Lessons P4. The figures in this lesson are correct but not
very useful for physical experimentation, as described in Lesson P5 on
building a peeping house. They were drawn compactly, with the vertical
vanishing point much too close to the horizon. This was done so that
all construction could be fitted on one page. This exercise
calls for a construction in KSEG which can be wiggled into one position
for easy construction, as in the lesson, and again into a more realistic
position, suitable for building a peeping house.
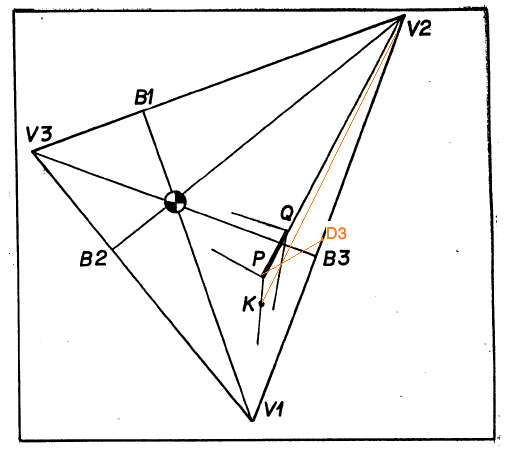
The figure at the right shows the construction lines in orange
that the lesson text describes, but which are not drawn into to original
figure.
\section{Exercise}
Based on an arbitrary triangle $V_1 V_2 V_3$ whose vertices become the
three vanishing points, complete the Thales triangles on all three sides
and determine the three diagonal vanishing points. This is your
perspective frame.
(You might save this much of the construction as a separate file in order
to use it later.)
Now choose an arbitrary point $P$, and second arbitrary point $Q$ on
the construction line $PV_2$. Now construct a cube based on this edge
as described in the lesson.
\section{Discussion}
Since you will need to understand this construction for the take home
examination for this section
of the course you should repeat this construction
for an initial edge \textbf{not} lying inside the perspective triangle.
You can drag your pont $P$ outside the triangle, but certain constructions
will not be drawn by KSEG. You'll have to redo those in order to draw all
visible sides of the cube.
\end{document}
\section{Introduction}
This exercise is nothing more than actually carrying out the recipe for
drawing a cube in perspective, given one edge (and a 3-pt perspective
frame), as in Lessons P4. The figures in this lesson are correct but not
very useful for physical experimentation, as described in Lesson P5 on
building a peeping house. They were drawn compactly, with the vertical
vanishing point much too close to the horizon. This was done so that
all construction could be fitted on one page. This exercise
calls for a construction in KSEG which can be wiggled into one position
for easy construction, as in the lesson, and again into a more realistic
position, suitable for building a peeping house.
The figure at the right shows the construction lines in orange
that the lesson text describes, but which are not drawn into to original
figure.
\section{Exercise}
Based on an arbitrary triangle $V_1 V_2 V_3$ whose vertices become the
three vanishing points, complete the Thales triangles on all three sides
and determine the three diagonal vanishing points. This is your
perspective frame.
(You might save this much of the construction as a separate file in order
to use it later.)
Now choose an arbitrary point $P$, and second arbitrary point $Q$ on
the construction line $PV_2$. Now construct a cube based on this edge
as described in the lesson.
\section{Discussion}
Since you will need to understand this construction for the take home
examination for this section
of the course you should repeat this construction
for an initial edge \textbf{not} lying inside the perspective triangle.
You can drag your pont $P$ outside the triangle, but certain constructions
will not be drawn by KSEG. You'll have to redo those in order to draw all
visible sides of the cube.
\end{document}