Exercise on Drawing a Checkerboard Floor
4jul10\begin{document} \maketitle
 \section{Introduction}
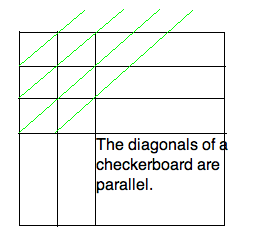
The simple observation that the diagonals of a checkerboard are
parallel leads to an efficient construction of a checkeboard in
perspective. It is done by sequential use of the edge and diagonal
vanishing points.
The above is an example of applying a genral principle which is elaborated
in Lesson P8 motivating the method of drawing a circle and measuring
a box. The principle is to infer a perspective construction of a figure
by observing geometric facts of the figure in reality. For a plane figure,
one studyies a drawing of the figure in a plane, as if seen from (far)
above the plane. This is called an \textit{orthographic projection}, or
more colloquially, an orthographic view.
\subsection{Not Using KSEG}
For this exercise you do not need KSEG at all, you could do it
with ruler alone. It can also be done efficiently in Paint/iPaint
because only straight lines need to be drawn through points.
\section{Exercise}
Propagate a given convex quadrilateral into a 5x5 checkerboard
design of your choice.
\subsection{Hint:} Start with an arbitrary convex quadrilateral and
construct the horizon with its vanishing points as in the previous
exercise. Now imagine laying a tiled floor by constructing an adjacent
square by drawing its diagonal first!
\subsection{Discussion:}
You may wonder about the purpose of such an easy exercise. It
constitutes one of the three different methods for laying out a
square (or rectangular) grid in perspective discussed in the lessons.
Which to apply in a praticular drawing depends on convenience, but also
on how accurate the drawing needs to be.
For the record, the three methods are these:
\begin{itemize}
\item Using the diagonal vanishing points of construction lines. \\
\item Using local \textit{division} and \textit{multiplication}
multiplications based on proportions. \\
\item Using the perspective frame. \\
\end{itemize}
The first is illustrated by this exercise. The second is best understood
by an example. It is used with a vengeance in Lesson P9 on constructing
perspective circles.The third is explained in detail and used in Lesson
P7 on measuring the proportions of a box given in perspective.
\section{Example}
\section{Introduction}
The simple observation that the diagonals of a checkerboard are
parallel leads to an efficient construction of a checkeboard in
perspective. It is done by sequential use of the edge and diagonal
vanishing points.
The above is an example of applying a genral principle which is elaborated
in Lesson P8 motivating the method of drawing a circle and measuring
a box. The principle is to infer a perspective construction of a figure
by observing geometric facts of the figure in reality. For a plane figure,
one studyies a drawing of the figure in a plane, as if seen from (far)
above the plane. This is called an \textit{orthographic projection}, or
more colloquially, an orthographic view.
\subsection{Not Using KSEG}
For this exercise you do not need KSEG at all, you could do it
with ruler alone. It can also be done efficiently in Paint/iPaint
because only straight lines need to be drawn through points.
\section{Exercise}
Propagate a given convex quadrilateral into a 5x5 checkerboard
design of your choice.
\subsection{Hint:} Start with an arbitrary convex quadrilateral and
construct the horizon with its vanishing points as in the previous
exercise. Now imagine laying a tiled floor by constructing an adjacent
square by drawing its diagonal first!
\subsection{Discussion:}
You may wonder about the purpose of such an easy exercise. It
constitutes one of the three different methods for laying out a
square (or rectangular) grid in perspective discussed in the lessons.
Which to apply in a praticular drawing depends on convenience, but also
on how accurate the drawing needs to be.
For the record, the three methods are these:
\begin{itemize}
\item Using the diagonal vanishing points of construction lines. \\
\item Using local \textit{division} and \textit{multiplication}
multiplications based on proportions. \\
\item Using the perspective frame. \\
\end{itemize}
The first is illustrated by this exercise. The second is best understood
by an example. It is used with a vengeance in Lesson P9 on constructing
perspective circles.The third is explained in detail and used in Lesson
P7 on measuring the proportions of a box given in perspective.
\section{Example}
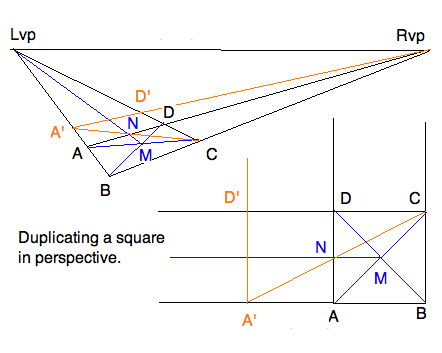 Given convex quadrilateral $ABCD$. We construct the right and left vanishing
points. We want the midpoint of the side \textit{AD}. For this, we first
find the center of the square in perspective. Note that in the orthographic
view the diagonals cross at the center $M$. Therefore the diagonals in
perspective locate the center in perspective (blue lines). In the orthographic
view, the line through the center and parallel to the sides crosses at the
desired $N$. In perspective, locate $N=(MLvp)(AD)$ (still blue.) Finally,
in the orthographic view, the (orange) line $(CN)$ crosses the
line $(AB)$ forming a right triangle in the ratio of 1:2. Therefore the
base seqment $A'A$ duplicatex $AB$, and erecting a parallel to $(AD)$ completes
the duplicated cube $A'ADD'$. The same construction in perspective achieves
the same end, in perspective.
\end{document}
Given convex quadrilateral $ABCD$. We construct the right and left vanishing
points. We want the midpoint of the side \textit{AD}. For this, we first
find the center of the square in perspective. Note that in the orthographic
view the diagonals cross at the center $M$. Therefore the diagonals in
perspective locate the center in perspective (blue lines). In the orthographic
view, the line through the center and parallel to the sides crosses at the
desired $N$. In perspective, locate $N=(MLvp)(AD)$ (still blue.) Finally,
in the orthographic view, the (orange) line $(CN)$ crosses the
line $(AB)$ forming a right triangle in the ratio of 1:2. Therefore the
base seqment $A'A$ duplicatex $AB$, and erecting a parallel to $(AD)$ completes
the duplicated cube $A'ADD'$. The same construction in perspective achieves
the same end, in perspective.
\end{document}