Although we have studied translations by exploiting their conveniently
simple defining formula, it is instructive to understand translations
as if they were "rotations" about an ideal point by an ideal angle.
This will emphasize the similarity of translations to rotations when
it comes to recalibration and conjugacy. Given a translation vector
$ D $ the direction perpendicular to $ D $ is an
ideal point $ D_\infty $ for this ideal rotation.
Recall that a translation, $ \tau_D $ has no fixed
points in the plane. Since a translation preserves perpendiculars and parallels,
$ D_\infty $ is the sole fixed point of this ideal rotation.
It does leave its ideal point fixed. For the concept of an ideal angle,
we shall simply use the displacement vector $ D $ itself.
We shall now mimic the wording and proofs of the previous lesson.
Note the factor of 2, and the direction of the displacement.
Also note that a line $ m $ passes through $ Q_\infty $
means that ` m _|_ D `.
Moreover, this "definition" is really a theorem we need to verify, since we have
already defined translations in terms of displacement vectors.
For instance, given the translation $ \tau_D $ and
any desired mirror `m _|_ D`, i.e. $ m = (MQ_\infty) $ and
$ (Mm) $.
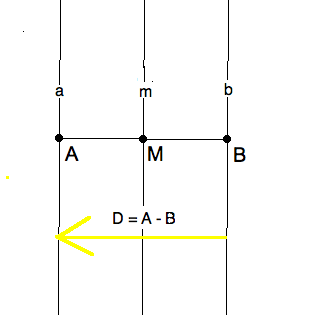
We can make $ m $ be the perpendicular bisector of a displacement
$ D = A - B $ in two ways.
-
Pick a point $ (Mm) $, a point $ B $ on the perpendicular
to $ m $ at $ M $ so that $ M - B = \frac{1}{2}(A-B) $
and reflect $ b $ in $ m $ to get $ a $.
-
Define $ a = \tau_{D//2}(m) $ and
$ \tau_{-D//2}(m) = b $. Note the half-vector and its sign.
|
Twas brillig and the slithy toves did gyre and gimble in the wabe. |
Question 1.
Why is $ \tau \ne \sigma_m $ even though both take $ b $
to $ a $ ?
Apply both isometries to the point $ M $ on $ m $. The
RHS leaves the point fixed. If the LHS would also fix $ M $ then
the translation would have a real fixed point. Indeed, you can
see in the figure that $ M^\rho $ is on the other side of $ a $.
Proof. From the answer to question 1 we know that
$ \alpha := \sigma_m \tau $ is not the identity. So property
R2 applies since $ \alpha $ has two fixed points; in fact, every
point on $ b $ first is translated to $ a $ and then
reflected back to $ b $. So
$ \sigma_m \tau = \sigma_b \implies \tau = \sigma_m \sigma_b $.
A similar argument for $ \omega = \tau \sigma_m $ settles the
"after mirror" cases. (Do it!)
An immediate application of this theorem and the conjugacy theorem for
reflections (CTR) is the following extension of CTR to translations.
Question 2.
Why don’t we just conclude that
$ \alpha \tau_D\alpha^{-1} = \tau_{D^\alpha}$, as we did in
$ \alpha \sigma_\ell \alpha^{-1} = \sigma_{\ell^\alpha}$?
This would be an error made in the text and we correct it here. An isometry
preserves displacements, not displacement from the origin. Unless, that
is, if the isometry fixes the origin, i.e. if it is an osometry.
Since we need
only one counterexample, recall that translations commute. So if
$ \alpha $ happens to be a translation, the LHS remains
$ \tau_D $. Then the equations would erroneously say that
$ D = D^\alpha $, which is not necessarily true.
Proof. Let $ m = perbis(A,B) $ and $ M = (m\ell_{AB}) $.
As we have already seen, $ \tau_D = \sigma_m \sigma_b $, where
$ a || m || b $ and $ (Aa), (Bb) $.
Then
$ \alpha \sigma_m \sigma_b \alpha^{-1}
= \alpha \sigma_m \iota \sigma_b \alpha^{-1}
= \alpha \sigma_m \alpha^{-1} \alpha \sigma_b \alpha^{-1}
= \sigma_{m^\alpha} \sigma_{k^\alpha} $
where we applied CTR in the last equation. Note that the mirrors
moved by $ \alpha $ remain parallel since isometries preserve angles.
In other words, $ m || b \implies m^\alpha || b^\alpha $ .
Thus we now know that the conjugate $ \tau^\alpha $ is another translation.
But why is it the expected one?
Since a translation is entirely determined by
the fate of any single point, we need only check what happens to the point
$ B^\alpha $. Under $ \sigma_{b^\alpha} $ it remains fixed on the
before mirror. Under the reflection in $ m $ it moves to $ A^\alpha $
on $ a^\alpha $. Hence $ \tau^alpha = \tau_{A^\alpha - B^\alpha $ and
we are done.
Question 3.
Knowing where an isometry moves 3 non-collinear points determines it.
How few points do you need to check for a reflection, rotation,
or translation?
The first assertion was an exercise applying the Barycenter theorem. For a
reflection you just need on point $ X $ that isn’t a fixed point, because
the $ perbis(A,A^\sigma) $ must be the mirrors. For a translation, any
point $ X $ will do, since $ \tau = \tau_{X^\tau - X} $. Rotations
need two $ P,Q $ . If one, $ Q $,
happens to be the fixed point, just measure the angle $ \angle PQP^\rho $.
We leave to you to discover the rotation from $ P,Q $ when neither is
fixed.
