1. Motivation

In the previous lesson we found that the most charming isometries were the composition (product) of three reflections in mirrors that are neither concurrent nor mutually parallel. In this lesson we shall analyze what such an isometry must be, and whether there is a ‘canonical’ of characterizing such an isometry.

As we shall see, such an isometry, $ \gamma = \sigma_r\sigma_q\sigma_p $, with $ \triangle pqr $ , is called a glide-reflections (glider for short) because it has a unique displacement vector $ D $ parallel to a unique mirror $ m $ so that $ \gamma = \tau_D \sigma_m = \sigma_m \tau_D $.

2. Anatomy of a glider

Let $ \gamma = \sigma_r\sigma_q\sigma_p $, with the three mirrors neither concurrent nor mutually parallel. Note that we are not requiring all three intersections $ (rq), (qp), (pr) $ to be finite. Two of the three mirrors could be parallel, as long as the third mirror crosses one of them. (Exercise: if two intersections were ideal, then one mirror would be the ideal line, which we excluded before.) We shall proceed with the assumption that $ B = (qp) $ is a finite crossing. We leave the other two cases for an exercise.

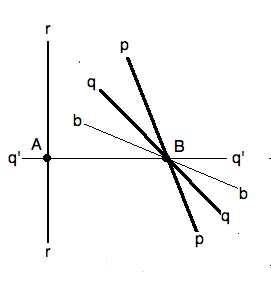
glider1.png

Given three mirrors $ p,q,r $, with the first two intersecting at $ (pq)= B $.

Rotate $ p,q $ to $ b,q' $ so that ` q' _|_ r`.

2.1. Step 1

If $ q _|_ r $ then relabel $ q = q', b = p $ and go to the next step. Otherwise, drop the perpendicular $ q' $ from $ B $ to mirror $ r $. Now recalibrate the rotation $ \rho_B := \sigma_q \sigma_p $ using $ q' $ as the preferred mirror through $ B $ and using a "before" mirror $ b $ so that $ \rho_B = \sigma_{q'} \sigma_b $.

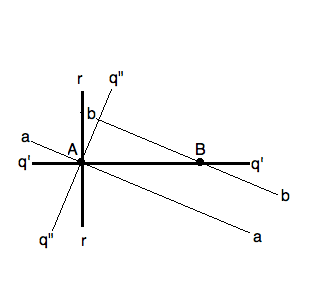
glider2.png

Rotate $ q',r $ about $ (q'r)=A $ to $ q'', a $ until $ q''_|_b $

2.2. Step 2

We now have $ \gamma = \sigma_r \sigma_{q'} \sigma_b $ where ` r _|_ q' `.

If $ q' _|_ b $ the relabel $ q' = q", r = a $ and go to the next step. Otherwise, drop the perpendicular $ q" $ from $ A = (rq') $ to $ b $. Now recalibrate the rotations $ \rho_A := \sigma_r \sigma_q' $ using $ q" $ as the preferred mirror through $ A $ and using an "after" mirror $ a $ so that $ \rho_A = \sigma_{a} \sigma_q" $.

Note that the recalibration preserves the angles: ` r_|_q'` hence ` a _|_ q" `. In fact, the rotation $ \rho_A $ is through $ 180^o $, and so it is the central reflection $ \sigma_A $ as well.

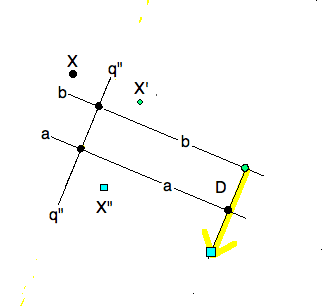
glider3.png

A isometry with three mirrors $ \triangle pqr $ recalibrated to be the

composition of three pairwise perpendicular mirrors $ a, q''m $ and $ m, b $

refactored as $ X' = \sigma_m $ and $ X''= \tau_D $ .

2.3. Step 3

Either by chance, one or two recalibrations we have recalibrated $ \gamma = \sigma_a \sigma_m \sigma_b $, where we have relabelled $ q" = m $. Moreover, looking back, we now also have the $ a || b $ and both are perpendicular to $ m $ .

glider4.png

Following the transformation of a point $ X $ by a glide-reflection,

(black dot to small square) reveals the symmetries of the most charming isometries.

2.4. Conclusion

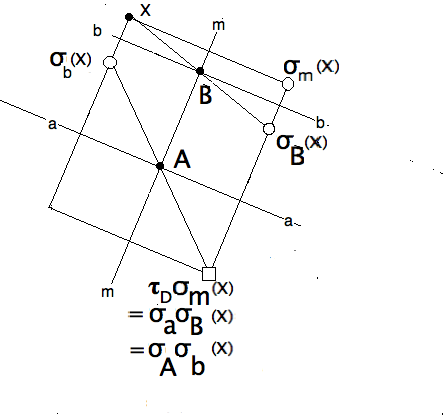
We can therefore write the glider $ \gamma = \sigma_A \sigma_b = \sigma_a \sigma_A $ as a reflection followed or preceded by a central reflection.

Moreover, a pair of reflections in perpendicular mirrors commute. (Exercise: use the conjugacy theorem). So swapping $ a,m $

$ \gamma = \sigma_m \sigma_a \sigma_b = \sigma_m \tau_D $

or swapping $ m,b $

$ \gamma = \sigma_a \sigma_b \sigma_m = \tau_D \sigma_m .$

It is from this the glider got its name, like a dance-step instruction: Take a step (translation) and change feet (reflection).

3. Classification Theorem

To show just how far we have come, we summarize the classification of isometries into four mutually exclusive sets (five actually).

Theorem.

If $ \omega $ is a bijective point transformation of the plane which preserves distances, $ (\forall P\ne Q)(|P^\omega - Q^\omega| = |P - Q| $ then $ omega $ is either the identity, or it is exactly one of a reflection, rotation, translation or glide-reflection.

Comment.

  • The identity is a group of one element.

  • The entire set of translations is a commutative group, if you consider $ \iota $ the trivial translation.

  • The set of all rotations with a common center form a commutative group as well, with $\iota $ the trivial rotation about every center.

  • Combining the rotations and translations into one set, it is also a group. Since these isometries all have charm 2, they are the sense preserving isometry group of the plane.

  • For each reflection, it together with $ \iota $ make a pretty small group. On the other hand, the reflections are the building blocks of all isometries.

  • The reflections and glide reflections have an odd charm, hence reverse orientation.