Logic Lesson on texPad
30jan11\begin{document} \maketitle \section{Introduction} In this (unfinished) lesson on material implication, as explained using texPad, we piggy-back two important issues in this course. \subsection{Implication is non-associative} It makes a difference where you put the parenthese when you have two implications in a row. Sometimes, there are as many as five. If you understand this lesson, you can work out the more complicated case.

 \subsection{Using texPad}
For many reasons, and even more tomorrow, we must find substitutes for the
traditional slate and chalk (or, whiteboard and marker) expository tool
in mathemetatics. The overriding principle to apply in judging such a
substitute is whether or not the technology makes its use no more cumbersome
and whether it is ubiquitous. Our version of this is texPad (see Advice/
for more details.)
\subsection{The argument}
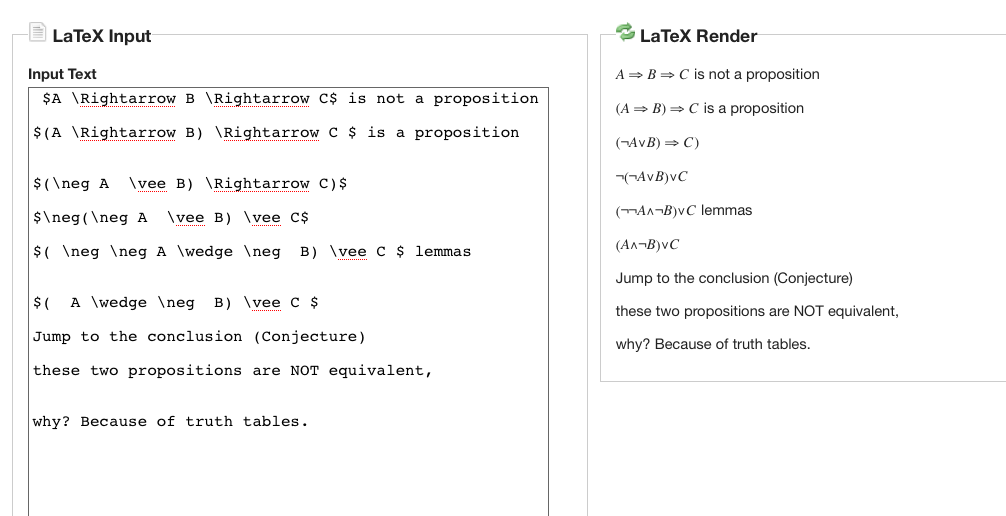
In the first panel we showed that if $A,B,C$ are propositions then
the compound proposition $D = (A\implies (B \implies C))$ is equivalent
to $E = (A \and B) \implies C $. This reformulation makes it easy to
understand, use, and even prove by contradiction. One of the intermediary
steps was
\begin{eqnarray*}
A \implies (B \implies C) & \sim & \bar{A} \or \bar{B} \or C \\
\therefore \neg (A \implies (B \implies C)) & \sim & A \and B \and \bar{C} \\
\end{eqnarray*}
Thus, to prove the first one true, the very least you need to do is show that
either $A$ is false, $B$ is false, or $C$ is true.
In the second panel, we simplify $(A \implies B) \implies C $ as much as
we can to get $(A \and \bar{B})\or C$. This does tell us that, for this
double implication to be true, either $C$ must already be known to be true,
or both $A$ must be true and $B$ must be false.
Since we end up with a disjunction of $C$ with a conjunction
$A \and \bar{B}$ we can go a little further.
The $\and$ and $\or$ operators are each distributive
across the other. (See the textbook or google it.) That means we can
rewrite
\begin{eqnarray*}
(A \and \bar{B})\or C&\sim & (A\or C) \and (\bar{B} \or C) \\
& \sim & (A\or C) \and (B \implies C) \\
& \sim & (\bar{A} \implies C) \and (B \implies C) \\
\end{eqnarray*}
for what that's worth. Perhaps a lawyer could use this equivalence to really
complicate a legal document.
\section{Conclusion}
It's easy to forget what the purpose of this lesson was, namely to show
that the two double implications are not the same. What makes material
implication so special is that there is only one 0 in it's truth table.
That is, only $(1 \implies 0)$ is false. All 3 other cases are true.
This suggests a quick test
\begin{eqnarray*}
A \implies (B \implies C)& \mbox{ versus } & (A \implies B) \implies C\\
0 \implies (0 \implies 0)& \mbox{ versus } & (0 \implies 0) \implies 0\\
0 \implies 1 & \mbox{ versus } & 1 \implies 0\\
1 & \mbox{ versus } & 0 \\
\end{eqnarray*}
which shows that they are not equivalent.
\subsection{Using texPad}
For many reasons, and even more tomorrow, we must find substitutes for the
traditional slate and chalk (or, whiteboard and marker) expository tool
in mathemetatics. The overriding principle to apply in judging such a
substitute is whether or not the technology makes its use no more cumbersome
and whether it is ubiquitous. Our version of this is texPad (see Advice/
for more details.)
\subsection{The argument}
In the first panel we showed that if $A,B,C$ are propositions then
the compound proposition $D = (A\implies (B \implies C))$ is equivalent
to $E = (A \and B) \implies C $. This reformulation makes it easy to
understand, use, and even prove by contradiction. One of the intermediary
steps was
\begin{eqnarray*}
A \implies (B \implies C) & \sim & \bar{A} \or \bar{B} \or C \\
\therefore \neg (A \implies (B \implies C)) & \sim & A \and B \and \bar{C} \\
\end{eqnarray*}
Thus, to prove the first one true, the very least you need to do is show that
either $A$ is false, $B$ is false, or $C$ is true.
In the second panel, we simplify $(A \implies B) \implies C $ as much as
we can to get $(A \and \bar{B})\or C$. This does tell us that, for this
double implication to be true, either $C$ must already be known to be true,
or both $A$ must be true and $B$ must be false.
Since we end up with a disjunction of $C$ with a conjunction
$A \and \bar{B}$ we can go a little further.
The $\and$ and $\or$ operators are each distributive
across the other. (See the textbook or google it.) That means we can
rewrite
\begin{eqnarray*}
(A \and \bar{B})\or C&\sim & (A\or C) \and (\bar{B} \or C) \\
& \sim & (A\or C) \and (B \implies C) \\
& \sim & (\bar{A} \implies C) \and (B \implies C) \\
\end{eqnarray*}
for what that's worth. Perhaps a lawyer could use this equivalence to really
complicate a legal document.
\section{Conclusion}
It's easy to forget what the purpose of this lesson was, namely to show
that the two double implications are not the same. What makes material
implication so special is that there is only one 0 in it's truth table.
That is, only $(1 \implies 0)$ is false. All 3 other cases are true.
This suggests a quick test
\begin{eqnarray*}
A \implies (B \implies C)& \mbox{ versus } & (A \implies B) \implies C\\
0 \implies (0 \implies 0)& \mbox{ versus } & (0 \implies 0) \implies 0\\
0 \implies 1 & \mbox{ versus } & 1 \implies 0\\
1 & \mbox{ versus } & 0 \\
\end{eqnarray*}
which shows that they are not equivalent.
Question1: Is this the only one of the 8 cases where they differ?
\end{document}