The Fifth Lesson on Analysis
The Bolzano-Weierstrass Theorem
last updated 1jul13 previously 10apr11, corrected 11apr11 with Hannah's help, typos removed 10apr12\begin{document} \maketitle
\section{Introduction}
We will make this the capstone theorem for the current edition of the course.
As a named theorem, it joins Euclid's Algorithm, The Pythagorean Theorem,
The Schroeder-Bernstein Theorem, Cantor's Cardinality Theorem, Weierstrass's
Diagonal Process, and Fermat's Little Theorem, as one of the classic theorems
every mathematics student should know how to prove sometime in their career.
\textbf{Theorem: In every bounded, infinite set of real numbers there
is a convergent infinite subsequence.}
\textbf{Example 1.}
Let $S = \{\frac{1}{n}\}$.
Clearly, $S$ is infinite and bounded by $0$ below
and $2$ above. Thus $S\subset (0,2)$. The sequence itself converges
to $0,$ which is not itself in $S$.
\textbf{Example 2. } Let $ S = \{(-1)^n + \frac{1}{n}\}$. Here there are
two convergent subsequences, the even-indexed members converge to $1$
and the odd ones converge to $-1.$ Neither is in $S$.
We proceed towards a proof by building up to it slowly,
and ultimately showing how to actually find the $limsup(S)$
and a subsequence converging to it.
\section{Subsequences}
Because of its prominent place here, we need to make the concept of a
\textit{ subsequence} of a \textit{ sequence} more precise. For this we,
temporarily, go back to the formal definition of a sequence as a
function
\textbf{Definition:} A \textbf{subsequence} of a sequence
$f: \mathbb{N}\rightarrow \mathbb{R}$ is the restriction of $f$ to
an infinite subset of $\mathbb{N}$..
Note that an infinite subset $S \in \mathbb{N}$ has the same cardinality
as the whole numbers, i.e. there is a bijection
$\sigma : \mathbb{N} \rightarrow S$. We use $\sigma$ because the bijection
depends on the subset $S$. Thus, our subsequence is itself a
sequence once we write it this way:
\[ f|S \mbox{ is the sequence } f\circ \sigma : \mathbb{N}\rightarrow \mathbb{R}\]
Question 1.
For a given infinite subset $S$ of whole numbers, use
the concept of a minium to find a \textit{ monotonic }
bijections $\sigma : \mathbb{N}\rightarrow S $. By monotonic we
mean that $i\lt j \Rightarrow \sigma(i) \lt \sigma(j) $.
There is no consistency on how to write a subsequence of a sequence $x_n$.
One ways is to write $x_{n_i} = f \circ \sigma(i) = f(n_i) $. Or we put
a prime on the letter so that $x'_n = f \circ \sigma (n)$.
Our textbook, while it discussed the notion carefully on p. 277 ,
avoids introducing yet another notation for this concept.
\section{Ingredients for the Soup}
\subsection {Binary Search}
This is a technique for finding real numbers that have a particular propery.
It is not unlike finite induction in some respects. Once you understand
the concept, and have written it into your Journal, add a paragraphs or two
on how it is similar to, and how it is different from finite induction.
Another concept you already know, decimal expansions, is related to binary
search. In fact, decimals are the outcome of what we might call a \textit{
decimal search.} Or, if you're comfortable with binimals, then a binary
search is exactly the calculation that generates a binimal with a given
property. Of course, none of these analogs actually defines a binary search.
And neither will we define it abstractly until after we have given some
examples.
\subsection{Limit points, the Liminf, the Limsup.}
Whenever a set (bounded or not) contains an infinute subesequence that
converges, we count the limit of the sequence among the \textit{ limit points}
of the set. In the two examples above, the first has only one limit point.
The second has two. Sets can have infinitely many limit points. And any one
of them may or may not be members of the set. If a set contains all of its
limit points, if it has any, we call is a \textit{ closed set }.
Question 2.
Show every point of the set $S = \mathbb{Q} \cap (0,1) $
( of rational numbers between $0$ and $1$ exclusive)
is a limit point of $S$.
Hint:For any rational $0 \lt r \lt 1$ consider the sequence $r_n = r +\frac{1}{n}$.
Obviously, $r_n\rightarrow r$, but not very $r_n$ needs to be in $S$. Use the
definition of limit to construct a subsequence \textbf{ which is} in $S$.
As an aside, reacall that we rejected the terms \textit{ infimum, supremum},
preferring the Anglo-Saxon \textit{ glb, lub}. And, we also felt cheated
having to use such a complicated concept, when a set had a minimal or
maximal element. Since we're really interested only in infinite sets in
analysis, it will be comforting to know that not only do bounded infinite
sets have limit points, but there always is a first one on the left,
and a last one on the right.
These are also called \textbf{ the } \textit{ limit inferior} and
\textit{ limit superior}. This terminology is easily confused with
\textit{ infimum, supremum}. In other words, if $limS$ denotes the set of
limit points and it is not empty, then $liminf(S)$ = min $limS$, and
$limsup(S)$ = max $limS$.
Recall that, for a subset $S\subset \mathbb{R}$ we just defined
$limsup(S) = max(limS)$ where $limS$ is the set of limits of
infinite subsequences in $S$, all provided each term makes sense.
By Bolzano's theorem we now know that every infinite bounded set
posseses limit points, i.e. $limS$ is not empty. It is not hard to
see that if $S \subset [a,b]$ then so is $limS$ because no elements
of $S$ can get outside this closed interval, let alone an infinite
and convergent subsequence. Thus $s=lub(limS)$ exists.
Suppose, for the moment we do not believe that $s = max(limS)$.
We can use Cantor's diagonal argument to show that it must be so
as follows. Recall, as an easy lemma to prove if you wish, that
a least upper bound of a set which is not also a maximum of the
set must have an infinite subsequence which converges to that
lub. So suppose we have such a sequence
\[s_n \in limS \mbox{ with } s_n \rightarrow s=lub(limS).\]
Then we have sequences of points $ \sigma_j^i \in S $
\begin{eqnarray*}
\sigma_1^1, \sigma_2^1, \sigma_3^1, & ... & \rightarrow s_1 \\
\sigma_1^2, \sigma_2^2,\sigma_3^2, & ... & \rightarrow s_2 \\
\sigma_1^3, \sigma_2^3, \sigma_3^3, & ... & \rightarrow s_3 \\
... & ... & ... \\
\end{eqnarray*}
It is not difficult to see that the diagonal sequence
\[ \sigma_1^1, \sigma_2^2, \sigma_3^3, ... \rightarrow s. \]
Hence $s \in limS $ and there is its maximum as well.
Everything we have just said about limsup hold for liminf and
the glb. The importance of Bolzano's Theorem will impress you
once you are told, and later shown that all the intermediate
value theorem you learned in the calculus depend on it for
their proof. And much more.
\subsection{Finding the limsup of a bounded infinite set}
The binary search we now conduct locates the limsup. In your journal you should
write the analogous binary search of the liminf. If you can do this, you have
understood the above discussion.
\subsubsection{The initial step}
For an infinite set $S \subset (a,b)$ we put the subscript $0$ on each of
the three letters.
\[ \mbox{ Step 0: } S_0 \subset (a_0,b_0) \mbox{ is infinite.} \]
Now let $m_0 = (a_0+b_0)/2$, the midpoint.
Recall that $S$ has infinitely many members. But maybe only finitely
many of them reside in $S\cap (m_0,b_0)$. If so, then there still
are infinitely many S's in $S_1 := S\cap (a_0,m_0)$. In this case, we
choose $a_1 = a_0$ and $b_1 = m_1$ and we can go to the next step
below.
But what if not? Namely, what if $S\cap (m_0,b_0)$ still has
infinitely many points in it? Then, we happily chose it for our $S_1$.
Set $a_1 = m_0$ and $b_1 = b_1$. And choose $S_1=S\cap (a_1,b_1)$.
Now, either way, we have the repeat of the hypothesis,
\[ \mbox{ Step 1: } S_1 \subset (a_1,b_1) \mbox{ is infinite.} \]
\subsubsection{The recursion}
There is nothing to stop us from repeating the argument above with
subscript $1$ replacing $0$, and then $2$ for $1$, and so forth.
\subsection{Collecting our wits}
Here's what we have done. We have a sequence of infinite subsets
\[ ... S_n \subset S_{n-1} \subset ... \subset S_2 \subset S_1 \subset S \]
bounded by intervals $(a_n,b_n)$ with $ 0< b_n -a_n < 2^{-n} $. We can
say that $S_n$ has \textit{ diameter } $ < 1/2^n$.
\subsubsection{Using infinity to good effect}
\begin{itemize}
\item We pick the first S-element $s_1 \in S_1$, \\
\item and an S-element $s_2 \in S_2$ different from $s_1$, \\
\item and an S-element $s_3 \in S_3$ different from $s_1, s_2$, \\
\item and an S-element $s_4 \in S_4$ different from $s_1, s_2, s_3$, \\
\item etc and so forth, by induction!
\end{itemize}
\subsection{Are we done yet?}
Yes, almost. If there is a limit $x = lim_{n\rightarrow \infty} s_n}$,
then we have found a subsequence of $S$ which converges. We would expect
this limit to be in all of the intervals of our binary search. Suppose
there is such a real number, $(\forall n)(a_n < x < b_n)$. We next
show that it fulfills the conditions of the limit of the $s_n$. Given
any $\epsilon > 0$, use that $\{2^{-n}\}$ is a null sequence.
Hence, for some $N$, $ 2^{-n} < 2^{-N} < \epsilon$ as soon as $n>N$.
Since both $x, s_n \in (a_n, b_n)$ we have that $|x-s_n|< 2^{-n} < \epsilon .$
Question 3.
Why must this $x$ so found be the limsup of $S$? Careful, this is
a difficult question. Think it through, writie it into your Journal, and
give a summary of your argument here.
\subsection{Moving right along}
But why should that sequence converge in the first place. Why should
there be a real number $x$ common to absolutely all of these nested,
shrinking open intervals we produced above? The answer is "because".
Namely, we need an axiom for the real number here.
\section{The Completeness Axiom}
As we saw several lessons previously, the existence of a lub for a
bounded set of numbers cannot be proved from the algebraic properties
of numbers. The rational numbers are not complete. For example,
$ S = \{ x \in \mathbb{Q}| x > 0 \mbox{ and } x^2 < 2 \} $ has no
lub in $\mathbb{Q}$ because for other reasons, we know that $\sqrt{2}$
is irrational.
In addition to the LUB-Principle, we have the notion of Toeplitz
sequences and their generalization, the Cauchy sequences. The
Continuity Axiom expressed in term of Toeplitz sequences implies,
for example, that inifinite decimals determine a real number. For
Cauchy sequences we merely claim that they we believe (that's what
we do with axioms) that they always converge to a unique real number.
\subsubsection{Using Cauchy Sequences}
Recall the definition that a sequence $\{x_n\}$ has Cauchy's property
if
\[ (\forall \epsilon > 0)(\exists N)(\forall n,m > N)( |x_n-x_m|<\epsilon)\]
Now in our binary search above we found a Cauchy sequence $s_n$. For,
$n,p, m:= n+p$ we have by the triangle inequality
\begin{eqnarray*}
|s_m-s_n| & = & |s_{n+p}- ... + s_{n+2}- s_{n+1} + s_{n+1}- s_{n}| \\
\mbox{ triangle inequality } & \le & |s_{n+p}-s_{n+p-1}|+ ... + |s_{n+2}- s_{n+1}| + |s_{n+1}- s_n| \\
\mbox{ binary search } & \lt & \frac{1}{2^{n+p-1}}+ \frac{1}{2^{n+p-2}}+ ... + \frac{1}{2^{n+1}}+ \frac{1}{2^n} \\
\mbox{ algebra } & = & (\frac{1}{2^{p-1}}+ \frac{1}{2^{p-2}}+ ... + \frac{1}{2} + 1 ) \frac{1}{2^n} \\
&\lt & 2 \frac{1}{2^n} = \frac{1}{2^{n-1}} \rightarrow 0 \\
\end{eqnarray*}
\subsection {Play it again sam .... }
Here's another way of phrasing this argument:
\begin{eqnarray*}
- \frac{1}{2^n} & < &s_{n+1} - s_n < \frac{1}{2^n} \\
- \frac{1}{2^{n+1}} & < &s_{n+2} - s_{n+1} < \frac{1}{2^{n+1}} \\
... & & ... \\
- \frac{1}{2^{n+p-1}} & < &s_{n+p} - s_{n+p-1} < \frac{1}{2^{n+p-1}} \\
\mbox{ adding } & & ... \\
- \frac{1}{2^n}(1+\frac{1}{2}+ ... + \frac{1}{2^{p-1}}) & < &s_{n+p} - s_{n} < \frac{1}{2^n}(1+\frac{1}{2}+ ... + \frac{1}{2^{p-1}}) \\
-\frac{2}{2^n} & < &s_{n+p} - s_{n} < \frac{2}{2^n} \\
\end{eqnarray*}
So, by \textit{ Cauchy's Completeness Axiom } we have convergence.
\subsubsection{Using Toeplitz Sequences}
We shall not give the general argument here. But a special case makes
really good sense. Suppose that $S\subset (0,1)$. Then all of the midpoints
$m_i$ are binary points, of the form $\frac{k}{2^i}$. Suppose we had
kept track of choosing the right or the left half interval by adding on a
binimal digit $0$ or $1$ depending on whether we chose the left or the
right interval.
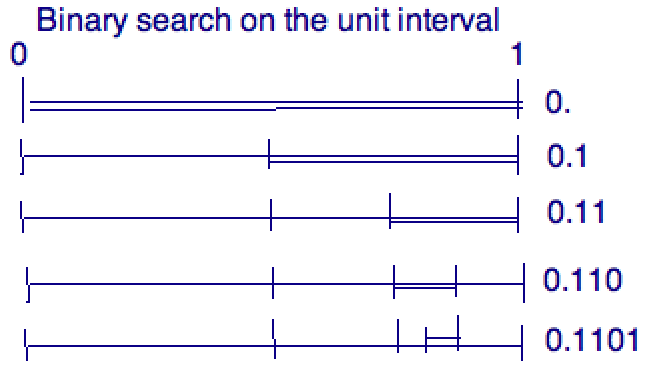For example, if we had the binimal $0.1101$, this
would mean that we found infinitely many S's in
$(0.1,1.0)$ and $(0.11,1.00)$ but in $(0.111,1.000)$ there were only
finitely many S's.
And that's why we chose the left half interval, which is $(0.110, 0.111)$.
The last $1$ just says that, once again, we found $(0.1101,0.1111)$
to have infinitely many elements. Etc and soforth. We get a binimal
number that way, and, by Toeplitz's Axiom, this represents a unique
real number.
Question 4.
Explain in words what $0.904$ would mean in a decimal search.
\subsection{Using the LUB Axiom}
If we insist on using the LUB Axiom, as the book does, then yet
another argument would need to be constructed. See the text book for one.
\section{Second Thoughts}
Actually, there is a sublety here which we choose to ignore in this
``elementary" introduction. However they are stated, LUB, Cauchy or
Toeplitz, the argument should really involve only rational numbers.
We shall happlily leave such complications for the first \textit{ real
analysis} (pun intended) course you will take in the future.
\subsection{Why a Cauchy Sequence Converges}
Cauchy's form of the \textit{ Completeness Axiom} says that it does. But
in a real analysis course you would have to show shat all Axioms are
equivalent. In particular, if we chose the \textit{ LUB-Axiom } as our
starting point, the we would have to prove Cauchy's (and Toeplitz's) Axioms
as theorems. We add a proof of this as an illustration of our techniques.
You will not be examined on understanding what follows in this course. On
the other hand, you can try to understand it, and thereby gain a proper
comprehension of this lesson.
[To be included in a later edition of this page.]
\end{document}