The First Lesson of the Course
Commentary on Chapter 1 of D'Angelo-West Text
14jan11, 30dec11, 20may13\begin{document} \maketitle

Summary
In this lesson you will learn \begin{itemize} \item A vocabulary for the various styles of mathematical writing. \item Learn to consult Advice and acceptable homework formats for this course. \item The hierarchy of the arithmetic, geometric and harmonic means of two numbers, and it's geometrical derivation. \item How to address filecard questions and homework assigments. \end{itemize} \section{Introduction} Just as Chapter 1 of our textbook is an introduction-by-example to the entire book, this lesson is an example of the commentaries which begin each lesson of the day. \subsection{Dating conventions} Since using dates, like, 1/18/11, or 18jan11, or 20110118, is prone to error, we will refer to class days by a day-week format. Thus 18jan11 is Tuesday of the first week of classes: T1. Thursday this week is, by the way, written R1. \subsection{Style conventions} Since MA348 is a course on writing mathematics, style is important. On most occasions, I will prepare class notes and post them on the web either before or after class. The webportal for this course is linked to http://new.math.uiuc.edu. These notes will reflect three common styles in which mathematicians communicate with each other: \begin{itemize} \item \textbf{Plaintext}, also referred to as \textit{ascii}, has an alphabet which coincides with the symbols on the standard keyboard. You see the symbol you get using only a key, or a shifted key. \item \textbf{LaTeX} is Donald Knuth and Leslie Lamport's universal standard for technical typesetting. Learning the rudiments of this skill is a required parts of MA348. \item \textbf{HTML}, for Hypertext Markup Language, is the language of the World Wide Web (WWW). This is not required for MA348, but it is useful to understand it because these lessons are written in a combination of HTML and LaTeX, called MathML. \end{itemize} These styles are also referred to by the suffices \texttt{.txt, .tex, .html} respectively. There is another important derived format, called .pdf, which converts many file formats into a universally transmissible and readable format. Because many users of pcs no longer see the suffixes, we also refer to them as text, TEX, HTML and PDF file formats. But I recommend you set your pc to add the suffix to its listing of filenames (this is an option) because the usual associated icon is prone to misinterpretation. This document is an example of an .html (or HTML) file. Look at its url. It ends with the .html suffix. You can always read, copy, steal and edit the underlying .html code of a webpage with a Control-Left-Click (Mac) or Right-Click (PC). This keypress drops a menu on which you choose "View Page Source". We abbreviate such an instruction thus: \texttt{ (CTL+LFT) > View Page Source } and \texttt{ (RIGHT) > View Page Source} The parentheses identify the key(s) to be pressed. The phrase refers to the text appearing somewhere on the resulting manu (drop down, control bar, etc). \subsection{Plaintext} In email you should always use plaintext because other formats, such as those used by Microsoft .doc, .rtf etc use codes for symbols which are often unreadable elsewhere. Indeed, such invisible codes associated with socalled "rich text" contaminates some applications we use in this course. To not copy and paste text produced in such processors unless you have first cleaned them of non ascii codes. To produce plaintext all you will need is a text editor. Here follows an online question, called a "filecard". You should aswer such questions as you read the lesson. Write your answer into your Journal. Once you are told that the filecard feature of these lessons is again operational, you should also enter your answer into this online feature, and expect feedback from the instructor within a few days.
Question 1: What is the title of this webpage? Hint: Look at its Source.
\subsubsection{Text Editors}
Many wordprocessors, such as Microsoft Word, are also an editor and can
produce plaintext documents if you tell them to do so.
Simple editors, such as Wordpad (PC), or Bean (Mac), naturally produce plaintext,
unless you force them to do otherwise.
Never save plaintext as "enriched text". Enriched text is a
Microsoft format that contains invisible control codes.
Plaintext contains only
printable characters (these are the 128 characters in the 7-bit
ascii code, for those of you who know what that is.) A good, and free editor for
Windows is Wordpad, and Bean is a free editor for macs .
But you are welcome to take this opportunity to learn a useful editor,
such as VIM (google vim). To write LaTeX documents you
need an editor because .tex documents can only handle plaintext.
\subsection{HTML}
Web documents also are written in plaintext. They contain instruction to
your webbrowser to convert them to the web format.
Although web documents are usually created with dedicated software to
produce pretty webpages, I encourage you to write and edit your webpages
using a plaintext editor instead. In addition to interpreting your
.html instructions, contemporary full feature webbrowsers, such as Firefox,
can interpret other languages, such as Javascript and
even more important for us, MathML. This feature allows us to
combine the mathematical typesetting features of LaTeX with the ease
of editing and distributing WWW documents. This topic is continued on
special pages the Advice section of our class web.
As of this writing, Google Chrome is on the verge of supporting MathML.
By the time you read this, it may have come true. Apple's Safari and
newly, Internet Explorer don't yet, or no longer support MathML. You will
have difficulty reading the lessons if you try to use these browsers.
Firefox downloads free on all platforms, PC, Apple and Linux. Use it!
You can always tell that you're looking at an HTML document by the profuse
use of phrases between "angle brackets". Angle brackets are the "less than"
and the "greater than" symbols from mathematics. In HTML (and XML) they
have the special meaning that the phrases written beween them is part of
the meta-language. The are command to your computer to do something. Text
not enclosed by angle brackets in an HTML document mean what they say.
\subsection{LaTeX}
A second lesson entirely devoted to LaTeX will follow this one. Read
ahead by perusing the Advice pages.
\section{About the Subject Matter}
To write mathematics and prove theorems you have to first learn to
\textit{read mathematics}. Here is some strong advice on how to read
math:
\begin{itemize}
\item Do not use highliners to deface your textbook. It wrecks its resale value.
\item Read with your hand! Have a handy pen and pad of paper next to your computer.
\item Date the pages you write and label for cross reference.
\item Keep your stray pages where you can find them, e.g. 3R binder.
\item When you understand what you have read, write an entry into your
course \textit{Journal.} You will use you Journal not only to study, but also
to collect your knowledge for the tests in the course.
The Journal has its own pages in the Advice webtree. Read them!
Question 2: Why should your Journal be a bound composition book, and not be a
spiral notebook, or composition book with glued pages?
Question 3: Why is a 3R binder not acceptable for a Journal? (You will
not be permitted to use such a "journal" on the exams.)
\item Read mathematics in three passes:
\begin{itemize}
\item \textbf{Skim: } Skip the formulas, read the plaintext, don't try to
follow the proofs. Check out the examples. Look at the pictures.
\item \textbf{Read:} Identify what you don't understand. Mark it down on
paper. Follow a proof by writing notes. Fill in the details left out
in the text. Think up an example, if none are provided. Do some of
the easy exercises. Write down clearly what you do not understand
and use it when you ask questions online or in class.
\item \textbf{Study:}
When reviewing for a test, during a tough homework, or if you are
referred back to this passage from another passage you don't understand
right away, then you have to study the passage. Note that to study
does not mean just to memorize. Nor is studying the same as cramming.
The latter works only to refresh your memory before a test of things
you already know because you have studied them earlier. Because you
may use your bound and handwritten Journal on all your tests in this course,
cramming is useless. More useful is to carefully prepare your Journal
well ahead of the time you need it on a test. Before the test, edit and
correct your Journal entries. That is a good way to "cram"!
\end{itemize}
\end{itemize}
\section{Homework}
Homework assigments also have their own pages. All
assignments are labelled by the day they are announced as due, even if
for some reason they are collected at a later date, or if you are submitting
late assignments.
\subsection{Homework format}
The exact format for submitting your homework depends on
the particular circumstances of the course you're in. Any changes to the
following prescribed format will be announced in the first few weeks of class.
So consider this a guide. But always keep a copy of your homework solutions in
your Journal, so you can quickly transcribe them (photocopy?) them for grading.
\textit{ 20may13: The followig was the format for the online MA348 course.}
After the third week of classes you are expected to submit your homework
typset in LaTeX using texWins or some other LaTex typesetting tool. Your
termpaper for this course (20pc of your grade) must be composed in LaTeX.
You will learn all you need in this course. You do not need to consult extraneous
LaTeX tutorials. But you may, of course, provide you follow the formats and
rubrics in Advice on how to prepare our termpaper.
By the second week your homework should contain proper mathematical symbols and
equations. If you're using MS Word 2010 to prepare your homework, you should
use its Equations Editor, which understands LaTeX command language. Your
formulas and equations my be composed in texPad rather than the symbols editor in Word.
Just remember, we accept only PDFs, even it composed in Word.
The first assigment may be prepared in any readable fashion.
Keep your corrected work in your \textit{portfolio}
\subsection{The Portfolio} [This does not apply to online courses.]
Ordinarily, your Portfolio is simply the collection of all your own work
other than the Journal. When you consult with the TA or Instructore, bring
your portfolio and journal with you for reference. However, this term
(Spring 2012) we will experiment with an electronic online "portfolio"
which is far more efficient and convenient. How to use this will be
explained in class.
\subsection{Homework 1}
Chapter 1 of the D'Angelo-West text is meant as an inventory of your
mathematical readiness for this course. You are not expected to know
all of this material already, but you are expected to understand the
explanations. The chapter ends with 56
problems, all of which you should read
with a pencil and pad of paper at your side. In preparation for this
homework you should \textit{skim} Chapter 1 so see what's where. Submit a
sheet of paper on which you classify the 56 problems according to the
following rubric. We will spend class time going over the most popular
problems submitted.
\begin{itemize}
\item Which problems are \textbf{not arranged} in the order in which their
topics appear in the text?
\item Which of the problems look \textbf{interesting} enough to invest time
understanding a solution?
\item Which of the \textbf{practice problems}, marked (-), can you do right now?
\item Which of the \textbf{regular problems}, not those with a (!), would
you be unabe to do even with some studying?
\item (You may list the problems in order and mark them with an
\textbf{N,I,P,R} for "not in order", "interesting", "pratice", and "regular",
as appropriate.)
\end{itemize}
\subsection{Rules for Handwritten Homework}
For Online Courses, hand written work must be scanned to a non-color,
non-editable image format (.png, .bmp, .jpg). This can be inserted into
MS Word and then "printed" to a PDF for submission purposes.
You may write this first homework by hand. You may get a chance
to enter it into an online file on the day it is due. In the future,
you may submit your homework handwritten if there are extenuating
circumstances which prevented you from doing it in the prescribed format.
You should, at any event, ask permission to do so.
If you do write your homework by hand, here are the format rules:
\begin{itemize}
\item Write on college ruled paper.
\item Write only on one side of a sheet of paper.
\item Do not leave ragged edges from tearing the page out of spiral book.
\item Use ink (=ballpoint, fiberpoint, inkpen); do not use not pencil.
\end{itemize}
\section{Digest of the Algebraic-Geometric-Harmonic Mean Inequality (AGHM)}
 This review is an example of how to study a topic in our textbook.
\subsection{Rationale}
We only have 3 class periods, T1, W1, R1 to cover Chapter 1 of the text.
Almost everything in this chapter reviews mathematics you have
already learned, though perhaps not in the present detail. Since learning
\textit{ how} to learn mathematics is, in the long run, more valuable than
learning any particular piece of math, let's concentrate on some
inequalities treated in the text. The cross reference to the text is in
square-brackets.
\subsection{The Triangle Inequality [$\S$ 1.3]}
To prove that
\begin{eqnarray*}
||x|-|y|| \leq & |x \pm y| & \leq |x|+|y| \\
\end{eqnarray*}
the authors, here as elsewhere, pull tricks out of the hat. After that,
their proof is clear. So, to learn the proof, you commit the trick to
memory (and emphasize it in your Journal). But,
how do you discover such a trick in the first place? Read on!
\subsection{The AGHM Inequality [$\S$ 1.6]}
By definition, for two non-negative real numbers, $x,y \ge 0$, their
\begin{eqnarray*}
\mbox{arithmetic mean is } \frac{x+y}{2} &=& \frac{1}{2}(x+y)\\
\mbox{geometric mean is } \sqrt{xy} &=& (x \ \times \ y)^{\frac{1}{2}}\\
\mbox{harmonic mean is } \frac{2}{\frac{1}{x}+\frac{1}{y}} &=&
(\frac{x^{-1}+y^{-1}}{2})^{-1} =
\frac{2xy}{x+y} \\
\end{eqnarray*}
and each is greater than (or equal) to the next.
The D'Angelo-West text gives the algebraic proofs of the AGHM inequalities.
For completeness, we give geometric arguments here. You are responsible for both.
For many people, a geometric argument is more persuasive and easier
to remember because it has a figure associated with it.
But the algebraic argument is usually more rigorous, and hence preferred
by the authors of our textbook.
This review is an example of how to study a topic in our textbook.
\subsection{Rationale}
We only have 3 class periods, T1, W1, R1 to cover Chapter 1 of the text.
Almost everything in this chapter reviews mathematics you have
already learned, though perhaps not in the present detail. Since learning
\textit{ how} to learn mathematics is, in the long run, more valuable than
learning any particular piece of math, let's concentrate on some
inequalities treated in the text. The cross reference to the text is in
square-brackets.
\subsection{The Triangle Inequality [$\S$ 1.3]}
To prove that
\begin{eqnarray*}
||x|-|y|| \leq & |x \pm y| & \leq |x|+|y| \\
\end{eqnarray*}
the authors, here as elsewhere, pull tricks out of the hat. After that,
their proof is clear. So, to learn the proof, you commit the trick to
memory (and emphasize it in your Journal). But,
how do you discover such a trick in the first place? Read on!
\subsection{The AGHM Inequality [$\S$ 1.6]}
By definition, for two non-negative real numbers, $x,y \ge 0$, their
\begin{eqnarray*}
\mbox{arithmetic mean is } \frac{x+y}{2} &=& \frac{1}{2}(x+y)\\
\mbox{geometric mean is } \sqrt{xy} &=& (x \ \times \ y)^{\frac{1}{2}}\\
\mbox{harmonic mean is } \frac{2}{\frac{1}{x}+\frac{1}{y}} &=&
(\frac{x^{-1}+y^{-1}}{2})^{-1} =
\frac{2xy}{x+y} \\
\end{eqnarray*}
and each is greater than (or equal) to the next.
The D'Angelo-West text gives the algebraic proofs of the AGHM inequalities.
For completeness, we give geometric arguments here. You are responsible for both.
For many people, a geometric argument is more persuasive and easier
to remember because it has a figure associated with it.
But the algebraic argument is usually more rigorous, and hence preferred
by the authors of our textbook.
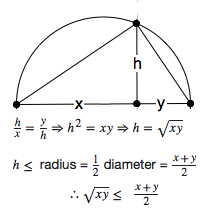 A description of the figure becomes a proof thus. In the semicircle
whose diameter is the sum of two lengths $x$ and $y$, inscribe the
right triangle whose altitude of length $h$ meets the diameter
where segment $x$ meets $y$. That this triangle is a right triangle is
known as \textit{ Thales' Theorem}. The two smaller right triangles
are each similar to Thales' triangle, and hence similar to each other.
This establishes the first equation. Arithmetic leads to the third
equation, which says
\begin{theorem}
The altitude of a right triangle is the geometric mean of the segments
on the hypotenuse subtended by the altitude.
\end{theorem}
On the other hand, the longest possible altitude of a Thales triangle
equals the radius of the semicircle. This establishes then second line
of inequalities in the caption of the figure. The third line follows
and we're done.
\subsection{Harmonic Mean}
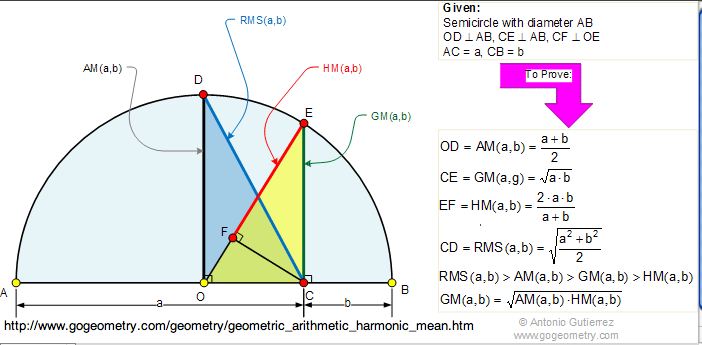
The figure by Antonio Gutierrez above tells the rest of the story geometrically. See if
you can describe his figure and so get a geometrical proof that the
harmonic mean is less than (or equal to) the geometric mean. Here we
present a \textit{ self-referential } algebraic proof, in the same style
as one derives the left half of the triangle inequality
$ ||x|-|y|| \le |x| + |y| $ is an application of the right half
$ |x \pm y| \le |x|+|y|$
We apply
\begin{theorem} The geometric mean of two non-negative quantities is less than (or equal) to their arithmetic mean (average). \end{theorem}
\textbf{Proof}
Apply the Arithemtic > Geometric Means inequality to the reciprocals of two
positive numbers thus:
\begin{eqnarray*}
\sqrt{\frac{1}{xy}} &\le& \frac{\frac{1}{x}+\frac{1}{y}}{2} \\
\therefore \sqrt{xy} & \ge & \frac{2}{\frac{1}{x}+\frac{1}{y}} \\
\end{eqnarray*}
So, now we have proved both inequalities in the AGHM
(Algebraic-Geometric-Harmonic Means Inequality). But note that Gutierrez
has a third inequality for the \textit{ root-mean-square
$\sqrt{ \frac{x^2 + y^2}{2}}$.
\section{Comments on the rest of the Chapter}
This chapter establishes lots of notational conventions.
If you're not yet familiar with their use, don't panic. We will be
using this notation for a whole semester, and by the end of it, you'll
know it by heart. In the meantime, refer back to this chapter repeatedly
until, well, until you no longer need to do it. Be sure you have a page
of unfamiliar notation explained in your Journal.
Beware of notational ambiguities involving number sets
\begin{eqnarray*}
\{-1,1 \}&=& \{x | x = -1 \ \or \ x=1 \}\\
[-1,1 ]&=& \{x | -1 \leq x \leq 1 \}\\
(-1,1 ]&=& \{x | -1 \lt x \leq 1 \}\\
(-1,1 )&=& \{x | -1 \lt x \lt 1 \}\\
\end{eqnarray*}
\subsection{Deep thoughts about sets}
Ponder the fact that for every set $A$ it is true that
$ A = \{ x | x \in A \} $. Does this define the set $A$ or doesn't it?
The previous is pop-Zen, an artifact of set notation. But the following
is not. It is \textit{Russell's Paradox.} Let us define a set $A$ to be
\begin{eqnarray*}
\mbox{extraordinary if } A& \in & A \\
\mbox{ordinary if } \neg(A& \in & A)\\
\end{eqnarray*}
Tell me, is the set of all ordinary sets ordinary or extraordinary?
What about the set of all extraordinary sets? By the way, the
symbols $\or, \neg$ mean "or" and "not" respectively.
\subsection{Number Systems [$\S$ 1.6] }
Skim (see above for what this means) the sections on number systems.
Either you already know this from earlier courses well enought to use
it correctly, or you will learn it in a proper course on the nature of
real numbers. This material is located here for cross reference
so your instructor of Math 444 or Math 447 can say that you have seen
this material in the prerequisites when she summarizes it in class.
\subsection{The Problems [ page 18]}
You already know how to solve problems, else you wouldn't
be in this course. And, it's too bad that all the problems in the text
appear at the end of the chapter, not in their place in the text. There
they would illustrate the material the immediately preceding material.
On the other hand, their placement at the end of a chapter allows you
to look at the problems first, and then decide what you need to review
in the preceding text. The Homework assigned above in this lesson motivates
you to actually skim the chapter, but also to at least read the problems.
\end{document}
A description of the figure becomes a proof thus. In the semicircle
whose diameter is the sum of two lengths $x$ and $y$, inscribe the
right triangle whose altitude of length $h$ meets the diameter
where segment $x$ meets $y$. That this triangle is a right triangle is
known as \textit{ Thales' Theorem}. The two smaller right triangles
are each similar to Thales' triangle, and hence similar to each other.
This establishes the first equation. Arithmetic leads to the third
equation, which says
\begin{theorem}
The altitude of a right triangle is the geometric mean of the segments
on the hypotenuse subtended by the altitude.
\end{theorem}
On the other hand, the longest possible altitude of a Thales triangle
equals the radius of the semicircle. This establishes then second line
of inequalities in the caption of the figure. The third line follows
and we're done.
\subsection{Harmonic Mean}
The figure by Antonio Gutierrez above tells the rest of the story geometrically. See if
you can describe his figure and so get a geometrical proof that the
harmonic mean is less than (or equal to) the geometric mean. Here we
present a \textit{ self-referential } algebraic proof, in the same style
as one derives the left half of the triangle inequality
$ ||x|-|y|| \le |x| + |y| $ is an application of the right half
$ |x \pm y| \le |x|+|y|$
We apply
\begin{theorem} The geometric mean of two non-negative quantities is less than (or equal) to their arithmetic mean (average). \end{theorem}
\textbf{Proof}
Apply the Arithemtic > Geometric Means inequality to the reciprocals of two
positive numbers thus:
\begin{eqnarray*}
\sqrt{\frac{1}{xy}} &\le& \frac{\frac{1}{x}+\frac{1}{y}}{2} \\
\therefore \sqrt{xy} & \ge & \frac{2}{\frac{1}{x}+\frac{1}{y}} \\
\end{eqnarray*}
So, now we have proved both inequalities in the AGHM
(Algebraic-Geometric-Harmonic Means Inequality). But note that Gutierrez
has a third inequality for the \textit{ root-mean-square
$\sqrt{ \frac{x^2 + y^2}{2}}$.
\section{Comments on the rest of the Chapter}
This chapter establishes lots of notational conventions.
If you're not yet familiar with their use, don't panic. We will be
using this notation for a whole semester, and by the end of it, you'll
know it by heart. In the meantime, refer back to this chapter repeatedly
until, well, until you no longer need to do it. Be sure you have a page
of unfamiliar notation explained in your Journal.
Beware of notational ambiguities involving number sets
\begin{eqnarray*}
\{-1,1 \}&=& \{x | x = -1 \ \or \ x=1 \}\\
[-1,1 ]&=& \{x | -1 \leq x \leq 1 \}\\
(-1,1 ]&=& \{x | -1 \lt x \leq 1 \}\\
(-1,1 )&=& \{x | -1 \lt x \lt 1 \}\\
\end{eqnarray*}
\subsection{Deep thoughts about sets}
Ponder the fact that for every set $A$ it is true that
$ A = \{ x | x \in A \} $. Does this define the set $A$ or doesn't it?
The previous is pop-Zen, an artifact of set notation. But the following
is not. It is \textit{Russell's Paradox.} Let us define a set $A$ to be
\begin{eqnarray*}
\mbox{extraordinary if } A& \in & A \\
\mbox{ordinary if } \neg(A& \in & A)\\
\end{eqnarray*}
Tell me, is the set of all ordinary sets ordinary or extraordinary?
What about the set of all extraordinary sets? By the way, the
symbols $\or, \neg$ mean "or" and "not" respectively.
\subsection{Number Systems [$\S$ 1.6] }
Skim (see above for what this means) the sections on number systems.
Either you already know this from earlier courses well enought to use
it correctly, or you will learn it in a proper course on the nature of
real numbers. This material is located here for cross reference
so your instructor of Math 444 or Math 447 can say that you have seen
this material in the prerequisites when she summarizes it in class.
\subsection{The Problems [ page 18]}
You already know how to solve problems, else you wouldn't
be in this course. And, it's too bad that all the problems in the text
appear at the end of the chapter, not in their place in the text. There
they would illustrate the material the immediately preceding material.
On the other hand, their placement at the end of a chapter allows you
to look at the problems first, and then decide what you need to review
in the preceding text. The Homework assigned above in this lesson motivates
you to actually skim the chapter, but also to at least read the problems.
\end{document}