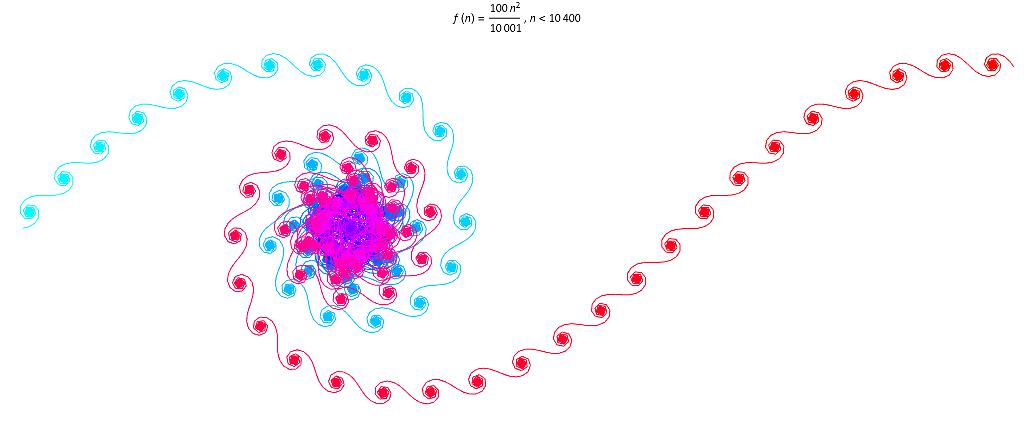
Visualization of Exponential Sums
by Junxian Li
For Math595, Fall 2015Exponential Sum
An exponential sum is defined as \[ \sum_{n=1}^N e^{2 \pi i f(n)},\] where f(n) is a real valued function.
A classical example of exponential sums is the complete Quadratic Gauss Sum given by \[ \sum_{n=1}^p e^{\frac{2 \pi i n^2}{p}}=\left\{ \begin{array}{ll} \sqrt{p} & p\equiv 1\bmod 4 \\ i \sqrt{p} & p\equiv 3\bmod 4 \\ \end{array} \right. ,\] where p is a prime number.
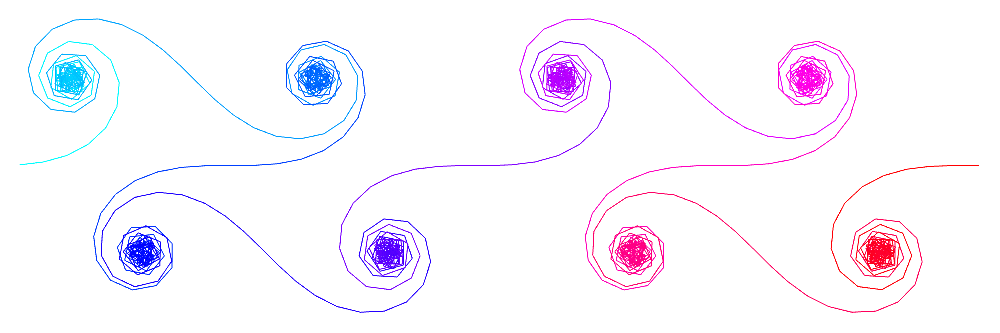
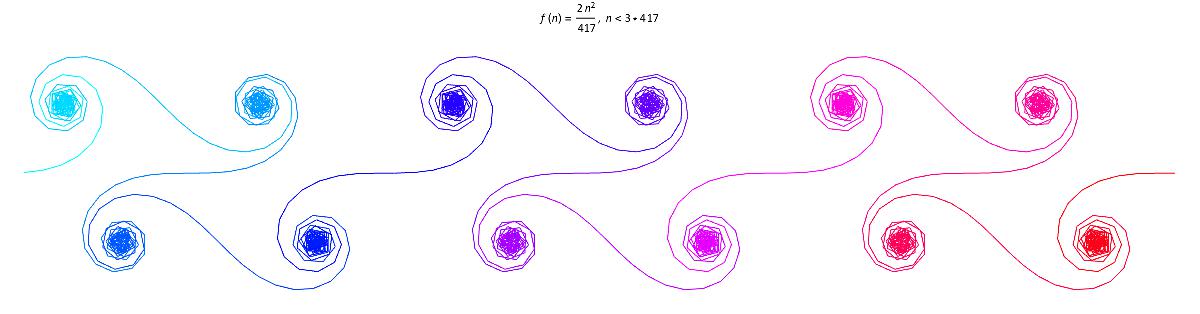
D. H. Lehmer has analysed the incomplete Gaussian sum \[ G_q(N)=\sum_{n=1}^N e^{\frac{2 \pi i n^2}{q}},\] where N and q are positive integers with N < q. Here is what they look like in the complex plane.
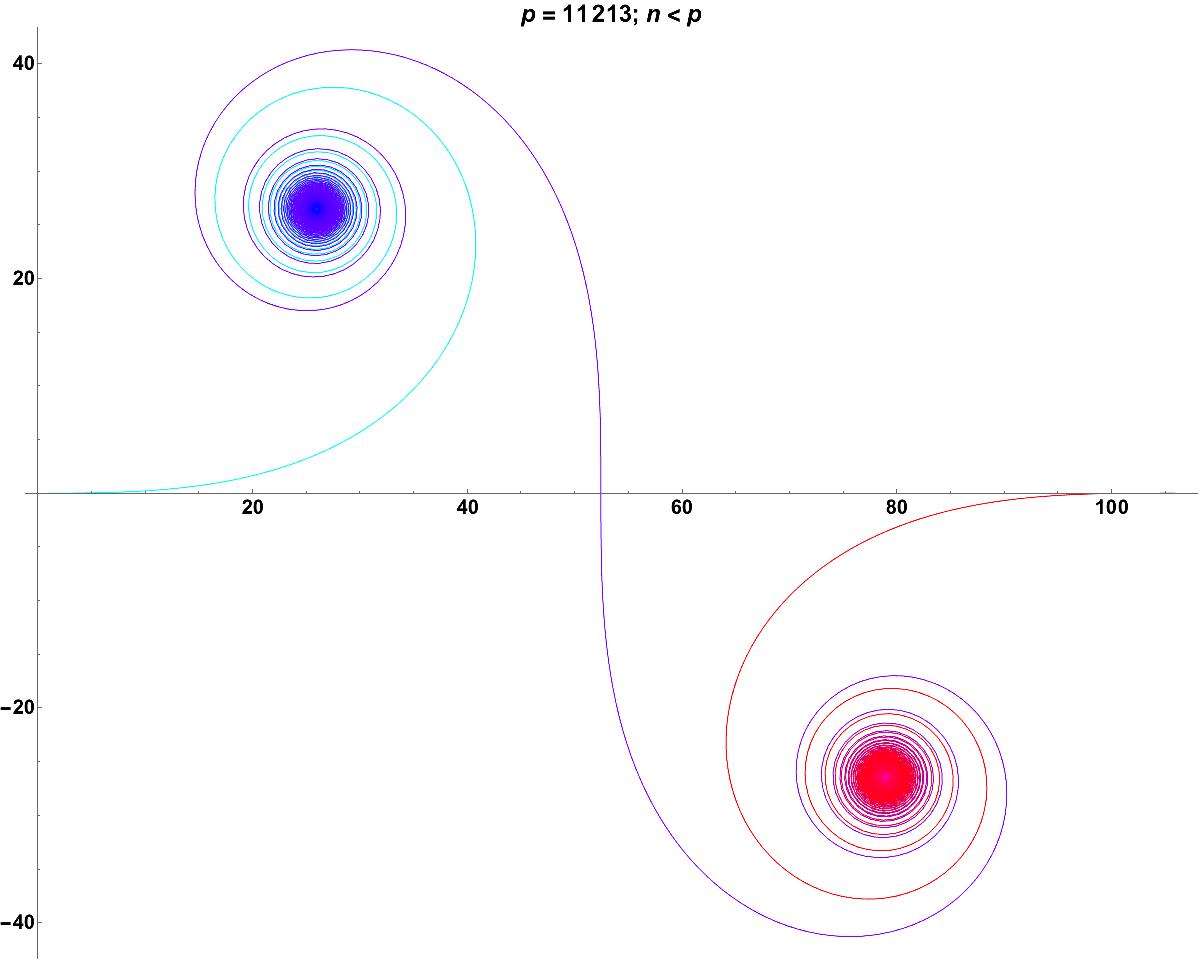
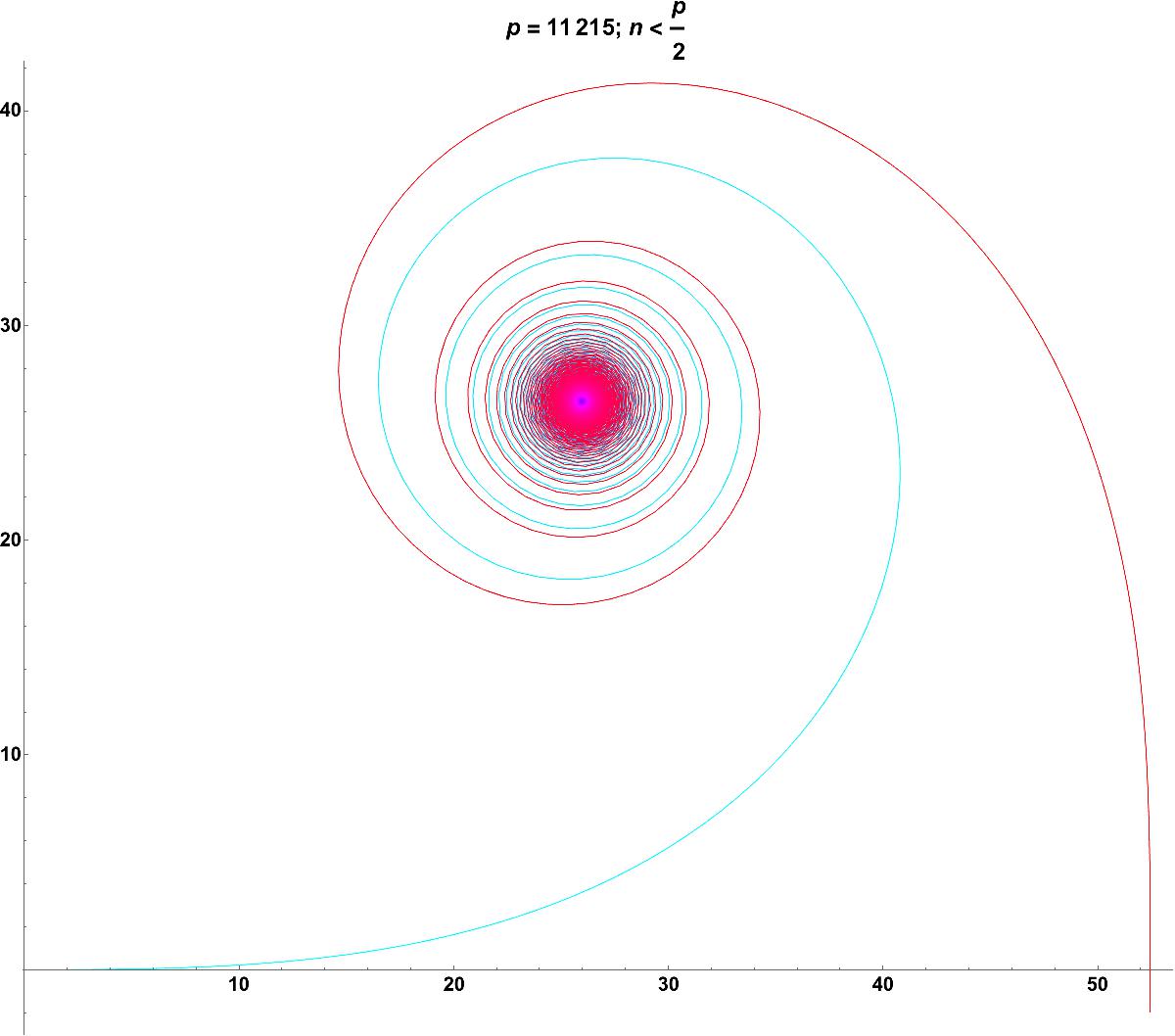
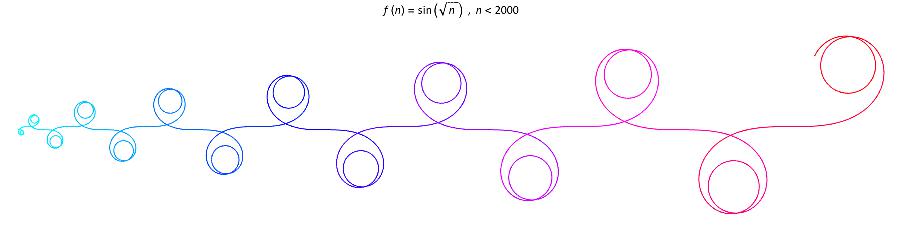
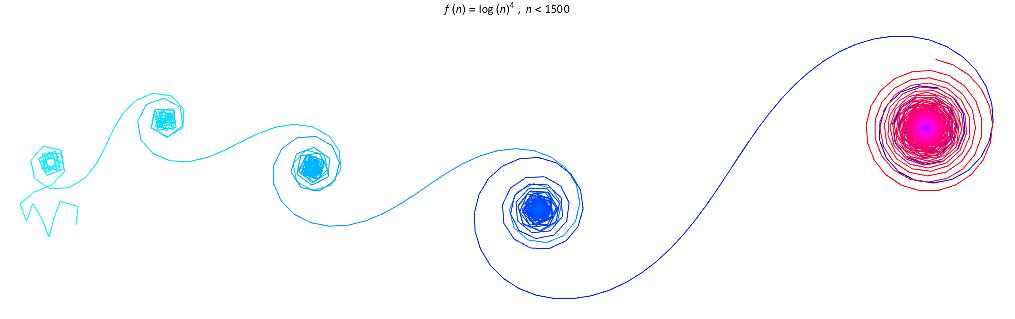
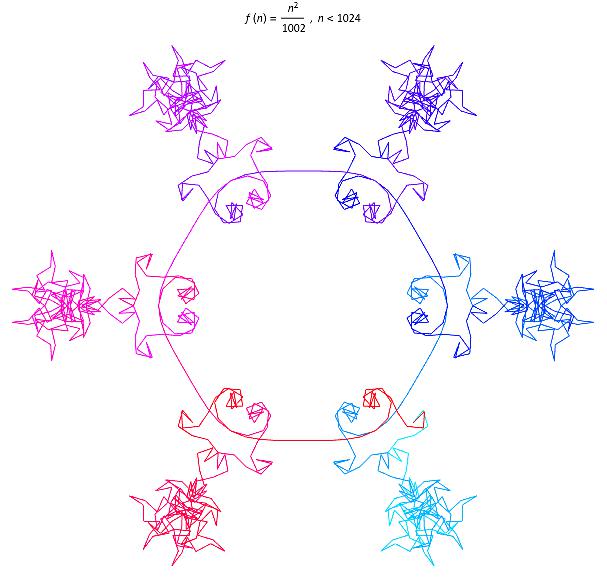
For different functions, the graphs look very different and can be very random.

Animation
References
(Loxton) The Graph of Exponential Sums
(Lehmer) Incomplete Gauss Sums