Math 280 Supplement to Friday, 22jan99.
Digression on Drawing.
In Two-Dimensions (2D)
You know already how to do this. But you might practice to develop some
style and shed bad habits from high-school. Do not "decorate" your drawing with
unessential clutter, such as putting arrows on your Cartesian axes, unless of
course you really do wan't to deviate from the natural direction.) Do label
you pictures with enough text to make it clear what you are depicting. Always
(except of on a test, of course) draw the picture on scratch paper first.
In Three-Dimensions (3D)
This is much more difficult since you were probably not taught the rudiments
of drawing in grade school. (Your teachers were probably much too busy
socializing you to teach you useful skills like drawing and singing.)
Here are two modes that are easy to learn. They serve different purposes, and,
unfortunately, they are not sufficient for every picture you may need to draw.
However, it's a start.
The Axonometric Method.
Suppose you need to *plot* (=technical use from now on, meaning to construct
on the basis of coordinate information) a figure. Start with 3 axes that give
the impression you're looking into the corner of a room. One axis should be
vertical, but the next should not be horizontal, because then the third
axis would come straight at you and be invisible. So draw it slightly below
horizontal to the right. The third axes points towards San Diego.
Mark a unit on each axis. Now you can draw every point with positive coordinates
by drawing lines parallel to the axes, by measuring off units (different in
each direction) and, if needed, by plotting (note the use of the term) the
curves of intersection of a surface in space with each of the coordinate planes.
For example, to plot the point, see
 Fig. 1.
Fig. 1.
the little numbers enumerate the sequential steps in drawing the picture,
_x = (1,3,2) = _i + 3 _j + 2 _k
0. Choses axonometric axes (3 lines and units).
1. "Let your fingers do the walking" from the origin to the tip of _i.
2. Add 3 _j by plotting a line parallel to the y-axis, 3 y-units long.
3. Ditto 2 z-units upward.
4. If you need to check your accuracy, complete one, 4, or the other, 4',
of the apparent rectangles (drawn as parallelograms) in the coordinate
planes (the walls of the room).
The "Ex-Post-Facto" method.
If you already know how the surface you are trying to draw is going to look
like, draw it first. Then introduce any coordinate axes you may need and
proceed axonometrically.
Example 1.
The function u = x^2 + y^2 has a bowl shape (parabolic surface)
 Fig. 2
Fig. 2
for its graph. Now add the axes to the already drawn picture.
Note that since the circular rim of the bowl, drawn here as an oval (an
ellipse) and *never* as a "cigar", is visible, therefore the bottom of
the bowl, which is at the origin, is invisible. Hence the gap between where
the horizontal axes come out from under the bowl.
Example 2.
For u = x^2 - y^2, which you know to be a saddle shape
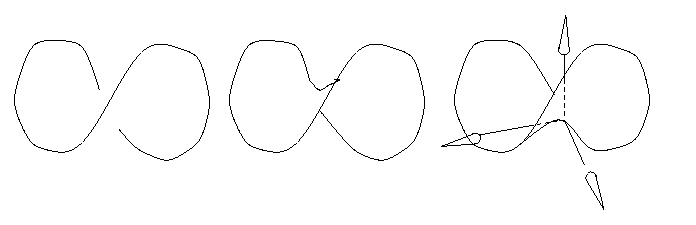 Fig. 3
Fig. 3
start by drawing the lazy-eight, representing the edge of a Pringle's potato
chip. Then finish the picture by revealing the underside, or the topside of
the saddle.
Note, finally, that for the horizontal axes, one is below and the other is
above the saddle.
Example 3.
Finally consider the surface u = f(x,y) where f(x,y) = x^3 - 3xy^2, which
is called the
 Monkey Saddle
Monkey Saddle
But before we consider drawing the 2D contours of this surface, we review
the calculations we went through in class to discover the derivative of f.
f(x+h,y+k) = (x+h)^3 - 3(x+h)(y+k)^3
= x^3 + {3x^2 h + 3xh^2} - 3(x+{h})(y^2 +{2yk+k^2})
which has been grouped to demonstrate continuity because
= x^3 + {A} - 3(x+{h})(y^2 +{B}) all three, A, h and B are null functions,
But we CAN expand each of these further:
{A} = (3x^2 + {A'})h where A' = 3xh + h^2 is again a null function,
{h} = ( 1 )h
{B} = (2y + {k}) k where {k} is again a null function.
So, rearranging all this in a more useful form, we continue the equality string
of f(x+h,y+k)=
= (x^3 - 3xy^2) + {A} -3{h}y^2 - 3x{B} -3{h}{B}
= f(x,y) + (3x^2 - 3y^2)h + (-6xy)k + ({A'} -3{B})h + (-3x{k}) k ).
Translating this into matrix notation we obtain
\delta u := f(x+h,y+k)- f(x,y) = [3x^2 - 3y^2 , -6xy]|h| + [Q_1,Q_2]|h|
|k| |k|
where both Q_1 and Q_2 -> when h,k -> 0.
(More)
 Fig. 1.
Fig. 1.
 Fig. 2
Fig. 2
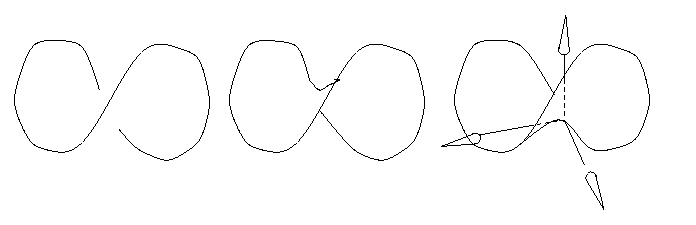 Fig. 3
Fig. 3  Monkey Saddle
Monkey Saddle