



Last edited 16dec15 by Alexandra Lamtyugina
alexandra.lamtyugina@gmail.com







Anyone who has ever had the pleasure of holding a piece of paper knows that it is possible to manipulate this seemingly two-dimensional object (with standard printer paper having a thickness of about 0.1 mm) into something which has a more appreciable third spatial dimension, whether it is by purposeful folding (origami) or by spontaneous artistic expression that normally accompanies frustration of trying to evaluate a very long and seemingly pointless mathematics problem on said piece of paper. As a long-time origami enthusiast and undergraduate researcher in the field of structural biochemistry, I especially appreciate the folding of simpler precursors into much more complex structures, which explains my motivation behind selecting the animation of folding along dihedral angles as my semester project for Math 198.

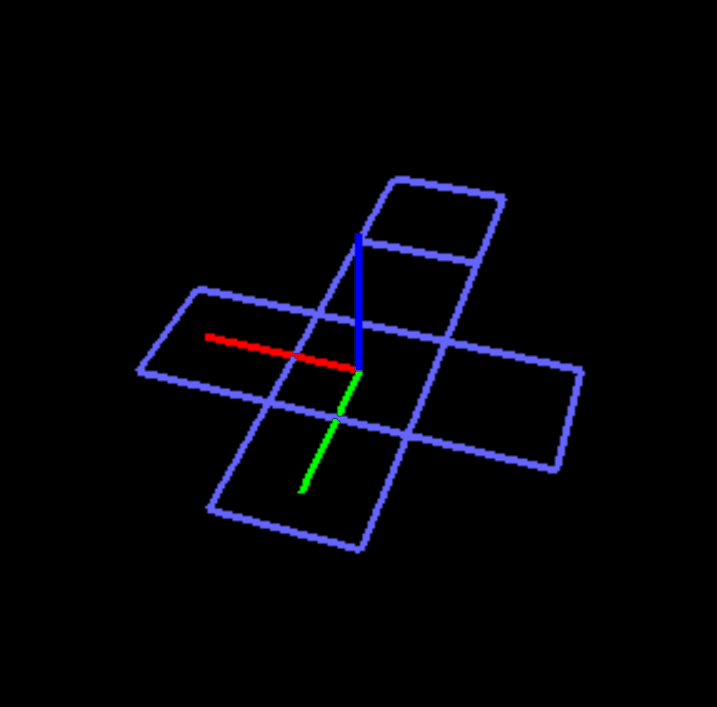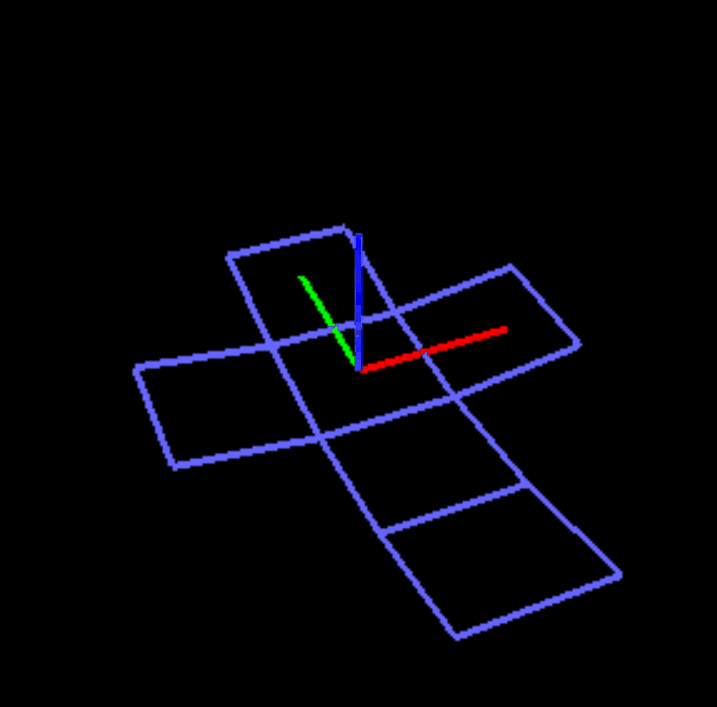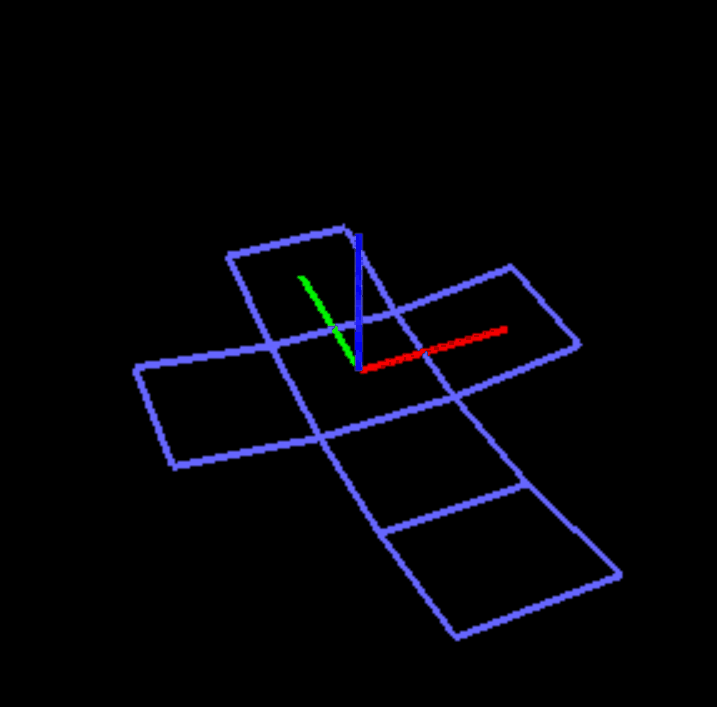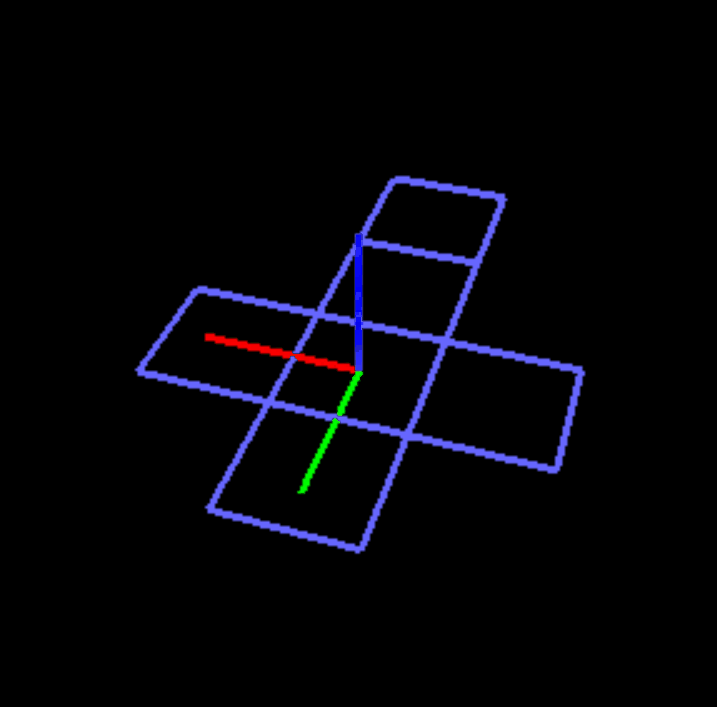
My primary goal was to create a dihedral folding animation of a flat net into its respective polyhedron. In brief, this was accomplished by defining the components (polygons) of the polyhedral net in separate vertex arrays, and then using glPushMatrix() and glPopMatrix() functions in order to transform these components with varying degrees of independence of other components, depending on the net and the components position within it. At its current stage, the project only provides an animation of the "triforce" net of a tetrahedron. However, work is currently being done on expanding the folding program so that it can generate unique nets for a cube and generate a folding algorithm based on the generated net.
My final project is written in C/OpenGL and compiled on the winaid compiler provided in the repository.
While I have greatly enjoyed working on this project, I feel that I could have accomplished much more had I had a firmer grasp on my programming language of choice, as well as the basics of linear algebra, both of which lie at the basis of animating the folding of polyhedra. Although the semester is officially over, I plan to continue experimenting with using computer animation in conjunction with my studies. MATH 198 has provided me with a solid introduction to the world of computer graphics, an area that I would not have been able to try out otherwise.
Below are some resources that have, whether directly or indirectly, helped me throughout this project: