Gravitation Stuck

Rachel Garrick

Math 198

Abstract

I have attempted to write a graphical program modeling gravitational interactions between masses, but with a twist! The objects are subject to an additional restriction, namely that they must remain stuck to a particular mathematical surface, which the user can choose and input.

My intention for my Hypergraphics project was to use Vpython to model the gravitational interactions between masses, simulating heavenly bodies. To make it more interesting, the bodies are restricted to surfaces whose equation the user can choose from a list of nice-looking ones. To start with, I worked from the Vpython example file “orbit.py,” which models two bodies orbiting each other. The math and code were relatively simple, and I was able to restrict them to a sphere by normalizing their position vectors and using the tangential component of their momentum vectors thus:

where x is position, p is momentum, and r is the radius of the sphere.

Here is a screenshot of the resulting program, orbit2body.py:

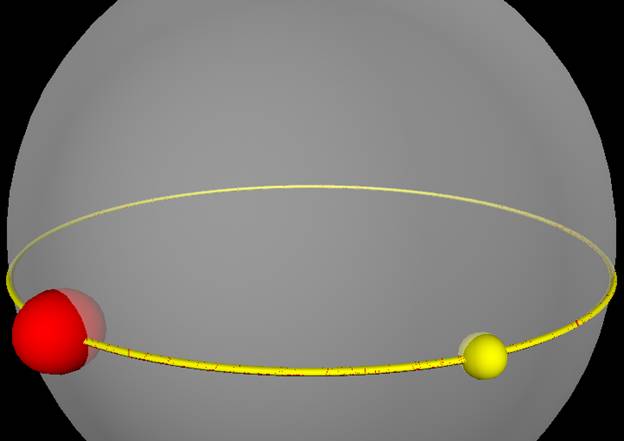
I also tried to adapt Stan Blank’s three body problem program from OpenGL to Visual, but it did not function. Beyond the sphere, I wished to view orbiting masses restricted to various surfaces, such as a paraboloid, a saddle, or a 3D function of sine waves. To this end, I modified this two-bodies-on-a-sphere program (a lot) to force the masses to return to the restricting surface using a version of Newton’s method known as gradient descent. This method works as follows.

The restriction is expressed as a level set of a function f(x) of position which equals zero. At each iteration, the gradient of this function is calculated at the natural position of the mass due to gravity only, which is somewhere off the surface. You follow the gradient back to the nearest point on the surface using Newton’s method:

or, more explicitly:

where t is the latest guess at the scalar amount you must go in the direction of the gradient to get back to the surface, x is the position of the mass, and f is the function of position whose level set f(x)=0 describes the restriction.

Unfortunately, this method does not converge for the saddle when the mass originates further from the surface than about 0.7 or so, as I found by experimenting further with the situation in the smaller program “please_saddle.py.” Furthermore, applying the method to the paraboloid and sine waves restrictions results in a so-far unexplained “divide by zero” error. In any case, the program has resulted in stationary spheres hanging out with the plotted surface, immobile, for every restriction except the sphere. However, in this still picture, you cannot even tell that it is not working!

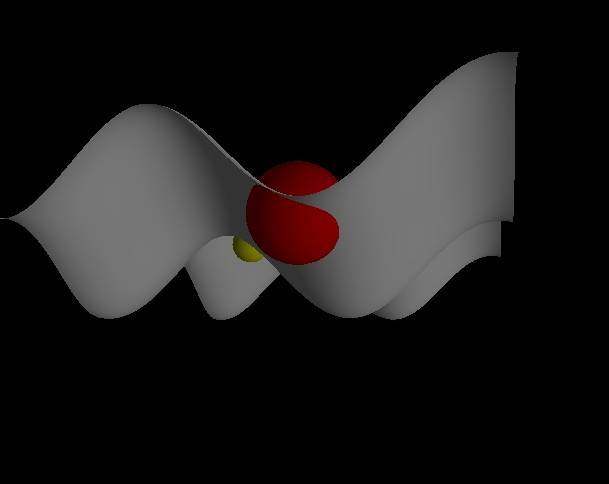
It is too bad, but Lord knows I tried.