Summation technique used in Pascal's tetrahedron

---

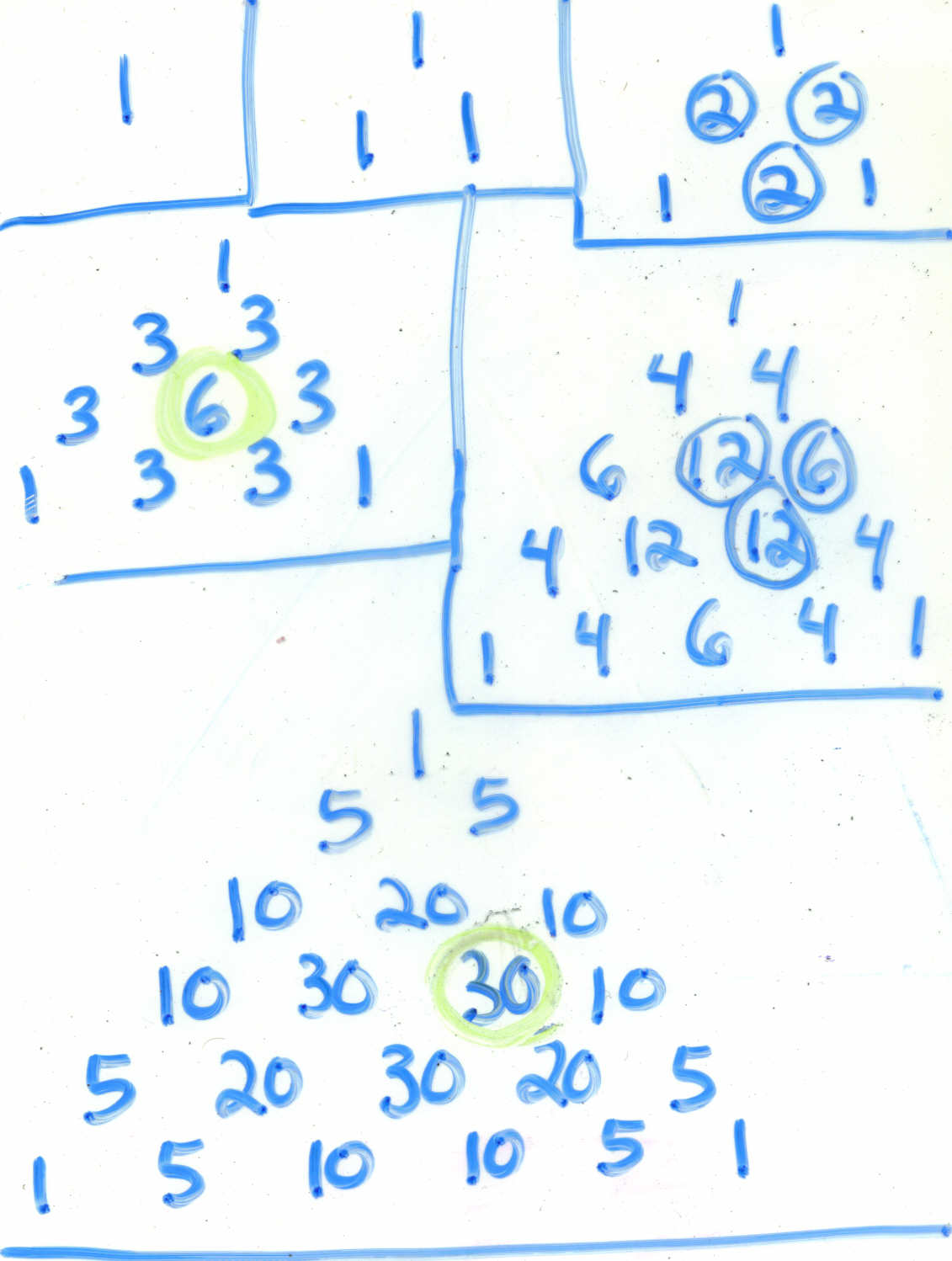
Allright, the way we find numbers in Pascal's tetrahedron is very similar to the procedure we used in the triangle. Intuitively, in 3D, we add three numbers to get the next number just as in 2D, we add two numbers to get the next number. It is a bit difficult to draw the tetrahedron in its natural state, so I must present it to you in different levels. The level containing only the "1" is the tip of the tetrahedron, the level containing the three "1"s is the next level down, and so on.

In this picture, the green number is the sum of three blue numbers that don't appear above Mr. Green in this particular drawing, but in a tetrahedron, they would be. For example, 30=12+12+6. Booyah!

---

Example 1 - Again the Kickball Example

Now instead of two teams, let's say we have three teams, X,Y, and Z. You again, as the great team organizer you are, go down the row of "n" people and assign each of them to one of these three teams. Your orders are to send "r" people to X, "c" people to Y, and "n-c-r" people to Z.

Let's assume we've done this process, and now we have to deal with the last guy. If you send him to Team X, you must have sent "r-1" out of the first "n-1" people to Team X, "c" to Y, and "n-c-r" to Z. If you send him to Y, you have already sent "r" to X, "c-1" to Y, and "n-c-r" to Z. Finally, if you send him to Z, you have sent "r" to X, "c" to Y, and "n-c-r-1" to Z. Sound confusing? Ultimately, (n)Choose(r)Choose(c)=(n-1)Choose(r-1)Choose(c)+(n-1)Choose(r)Choose(c-1)+(n-1)Choose(r)Choose(c). And that's all she wrote.

---

Example 2