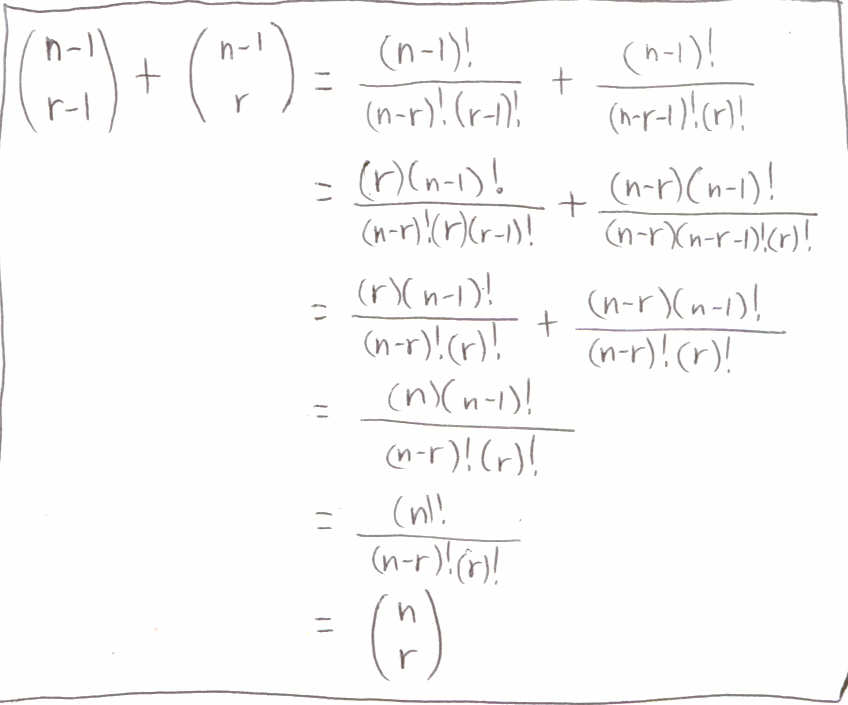Summation technique found in Pascal's triangle

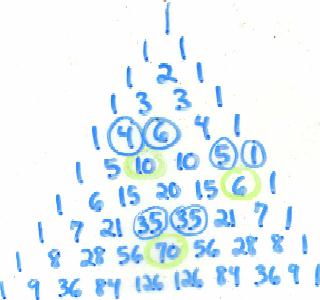
In the figure above, the number circled in green is the sum of the numbers circled in blue. Each green number has two and only two corresponding blue numbers.)

Allright, we all know how to generate the numbers in Pascal's triangle, but do we know why it works? Well, there are two ways to prove it as far as I'm concerned. For those of you out there who have more than one kind of learning style, I'm providing one example with words and one with symbols.

Example 1

OK, remember the glory days when you finally got to be captain of your 4th grade kickball team? Yeah, well I bet you never thought of how many different combinations of players your team could have! Anyway, let's say the orders are to pick "r" number of players for your team out of "n" people lined up hoping they will be picked.

But this is no traditional "one team picks one player, then another team picks one player." No. Instead, you, as the captain of your team, go down the row of people and either choose or don't choose each person.

Before you make your last pick (the poor soul), you will have gone through "n-1" people. If you choose the last guy, you must have chosen "r-1" people out of the first "n-1" people. If you decide you don't want him, well then, Mr. Big shot on grade school campus, you already have chosen your "r" people out of the first "n-1" people. Therefore, the number of different ways to compose a team in this manner is (n-1)Choose(r-1) + (n-1)Choose(r).

---

Example 2