Double-hockey stick theorem!

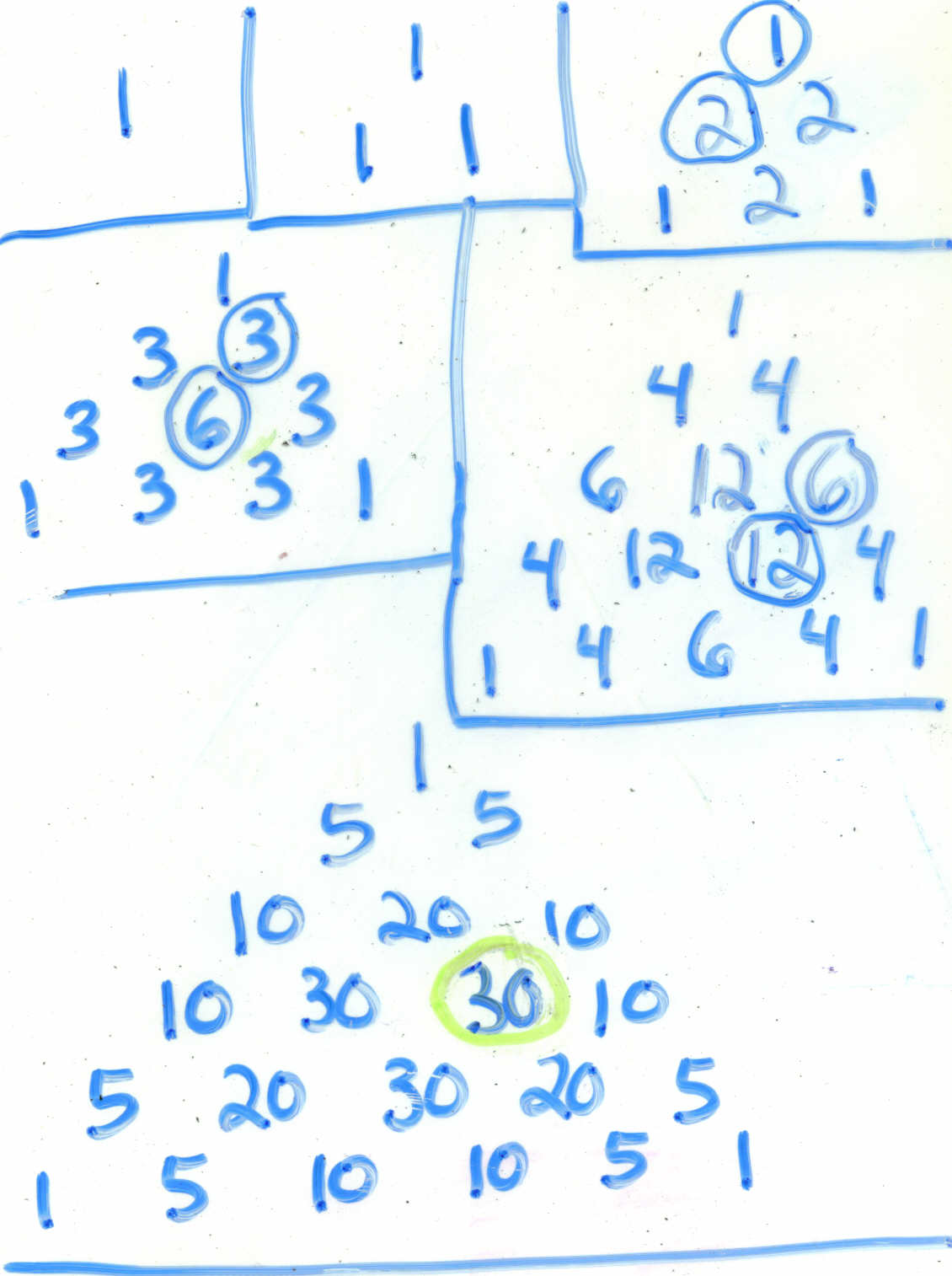
Allright, so you've mastered the 2D hockey stick. But are you ready for the NHL? Try 3D baby! Again, I have to draw the tetrahedron on many levels, and that's why I need a computer program to view this rule properly, but we can try anyway.

In the picture, 30=12+6+12 because of the summation technique I just proved. However, one of these 12s can be expanded into 3+3+6. And one of those threes can be expanded into 0+1+2. Since it would be pointless gab to try to expand 0, we are done. If you can visualize it (which I am still trying to do), these numbers should form two hockey sticks with the same orientation, side by side.