The goal of this project is to simulate the particles of an atmosphere under a gravitaional field. We know that the density of the particles in the positive vertical direction decreases exponentially. This exponential factor is the Boltzmann factor.
The Boltzmann factor can be used for any system where a small object is in contact with a large resevoir. The probabilty that the object is in a certian microstate is proportional the the Boltmann factor, e^(-E/kT), where E is the energy of the object, k is the Boltzmann constant, and T is the temperature.
In the case of this atmospheric system, the small object is an individual particle in the atmosphere and the large resevoir is the rest of atmosphere. It can be assumed that for any individual particle at a given altitude there is another particle with the same state of motion at a different altitude. Because of this, the energy of the particle can be simply represented as mgh. This makes the Boltzmann factor look like e^(-C*h) where C is a combination of all the constants.
This project is a simulation of a system that shows the density (which proportional to probability) of the particles in the horizontal direction taking on a negative exponential distribution under a gravitational field, and the expected Gaussian distribution with the gravity turned off.
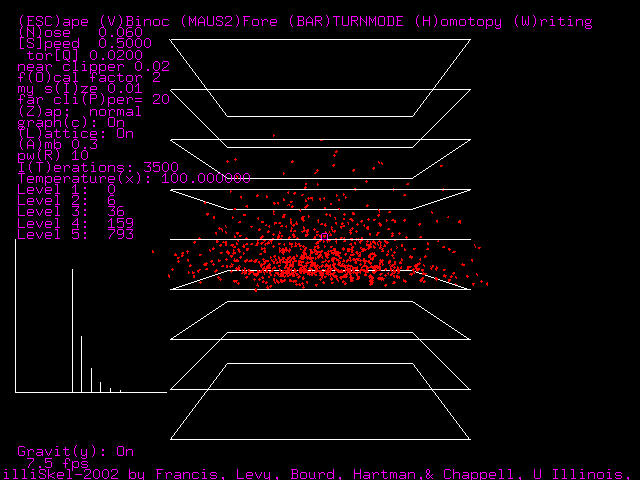
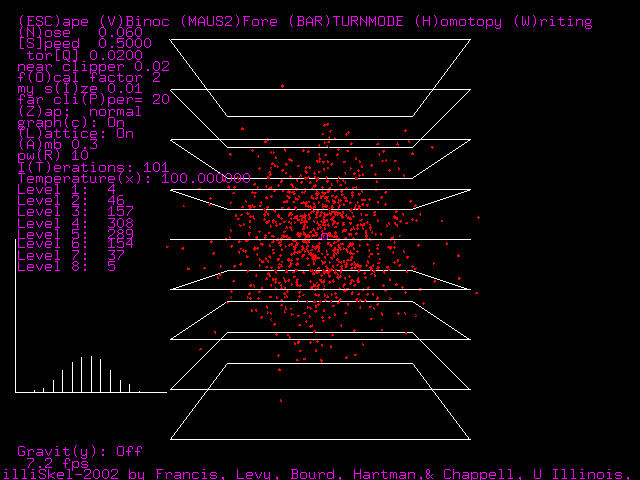
Here is an image of the simulation with the gravity turned off, note that the graph of the number
of particles on the vertical axis takes on a Gaussian distribution.