For my Math 198 project, I am investigating the biomechanics of figure skating; in particular, I am looking at jumps called "axels." Axels are the only jumps that take off from a forward outside edge. After take-off, the skater then rotates one and a half times (or two and a half or three and a half for double and triple axels) and then lands on a backward outside edge. Soon, I should have a video clip of me or someone else performing a single axel. We'll see...
Many variables that should be factored into the analysis of axels are: rotation speed, flight time, free leg position, take-off angle, vertical and horizontal velocity, rotational velocity, time to attain the rotating position, and jump height, as well as jump distance, take-off length, and skid length and width.
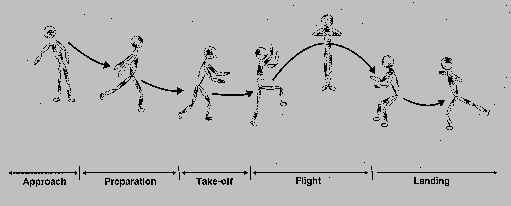
Before the skater can enter the jump, the skater must exert a force on the ice to begin rotation. In this sense the skater launches himself or herself in the air. Thus, the kinematic equations that deal with projectile motion can be applied to the skater.
Once in the air, the only force that acts on the skater is gravity. That is, no forces act to change the skater's angular momentum, which is equal to the skater's moment of inertia mulitplied by the skater's rotational speed (a.k.a. angular velocity). This is why skaters must create at much angular momentum before they take-off. Additionally, the poition of the body will affect angular momentum. That is, if the limbs are farther from the axis of rotation, in what is called "open" position, then the rotational speed decreases, and the moment of inertia increases. This compensation makes sense because angular momentum is conserved throughout the axel.
Rotational speed increases as the number of revolutions increases. So, a skater will have a higher rotational speed for a triple axel than for a double or single axel. And, as noted earlier, if rotational speed increases, so does the skater's moment of inertia. The angular momentum will stay the same.
At long last... I'm finished!!! However, my project did take a rather unexpected turn midway through contrstruction. Initially, I planned to focus on the physics of the axel and implement the concepts into a program where an articulated doll performed the jump. Unfortunately, there were many errors in my thinking and the idea had to be scrapped. I didn't mind too much, especially since getting the doll to move in a meaningful way was harder than I imagined. There were many small steps behind the scenes that make up just one jump.
The first progress I made was completing the doll's "skeleton." To complete this step, I needed to get a vague grasp of the idea behind pushing and popping matrices. This way, I could create a figure by choosing an origin, in my case the torso, and pushing on appendages, then popping back to the torso, and adding more appendages, and so on. Additionally, this technique used to create the skater was helpful when considering body motions in general. When you move your shoulder, the rest of your arm inevitably follows. In order to properly place the limbs in the correct position, I needed to translate the upper arms and thighs in the x direction. (For the other parts of the limbs, a translation in the x direction with a value of zero makes sense because your shins are aligned with your thighs.) The scaling was just a guesstimate, but I did give the skater rather large feet so it would be easier to see his or her orientation better.
The next part of the project I worked on was creating an ice surface for the skater. This was the easiest step of all; I just created a thin wire cube. Although, it was important to make this separate from the skater function because if they were combined, the ice arena would move with the skater!
After this came the task of creating a path for the skater to move along. I went down many avenues before a realistic path was generated. Professor Francis drew out a path and derived equations for the three different stages of the axel: preparation, jumping, and landing. We decided it would be easiest (and therefore, best) to have the skater's first two motions be linear and the last one "curvy." The preparation motion was fairly easy to create. The jumping part was more difficlut, as the skater needs to rotate about the y-axis one and a half times (a rotation of 3pi) and somehow move up and down along the y axis. Originally, the skater moved up and down in a path that used parametric equations, but later we changed the motion to be parabolic. The landing path was most easily programmed by considering it a circular motion.
Another major issue I needed to confront was time. The machines that we use in class run the program at about 70 frames per second. I knew that I wanted the user to input time and have that value influence the time the skater took to complete the axel. After many, many sessions with Professor Francis and Ben, we created a way to increment time considering the number of frames we consider (105, with 35 frames per part of axel) and the frames per second that the computer runs the program at.
The most difficult part of the program was figuring out semi-realitic movements that the skater could make. I ran into the problem of legs that went into very uncomfortable postitions behind the skater's head and arms that would slice through the torso (ouch!). Part of the problem came from the issue step vs. progress. Step is a function that takes in a change in value (when used in a glRotatef, it would be change in degrees of rotation) and a time at which this change would occur. After a week or so, I realized adapting every step function in rotate to have the time be multiplied by some form of current time divided by total number of frames was too crazy for me. Hence, the birth of the progress function. This allowed me to take in initial and final postions and initial and final times so the change in position would be gradual rather than jerky. Now comes the question, 'How did she know when and how to move the limbs?' Well, to be honest, I had no clue. I watched the video of myself, which will hopefully be posted on this website, and printed off as many frames of the video as I could. From there, it was mostly trial and error to see what looked believable.