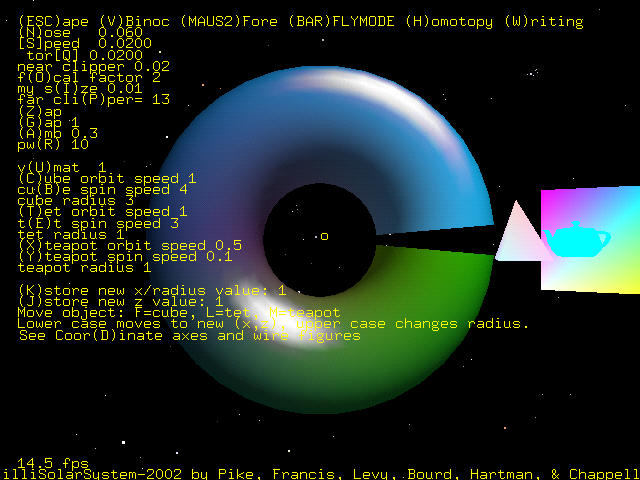

The arrangement is not quite that of a real solar system. The orbits are circular, not elliptical. Also, the objects are allowed to pass through one another. The numbers displayed for orbit speed are values of angular velocity. The actual velocity of an object is the angular velocity multiplied by the radius. The orbiting of the objects was first tried using Euler's Method. However, with this method, the radius of the objects continuously increased. The Gauss-Seidel method was then used, which resulted in a constant radius for each object.
The drawing of the cube and tetrahedron was hard-coded, while a built-in function was used to draw the teapot. These three objects spin about the y-axis. So that the spinning of the cube does not affect the orbit and spin of the teapot, the teapot has additional calls to the orbit and spin functions to compensate for the spinning of the cube.
The user of the program is allowed to view the arrangement of objects through the affine matrix and also through each of the objects. To view through the torus, cube, or tet, the matrix corresponding to the object is inverted. To view through the teapot, the teapot matrix and cube matrix are multiplied, and then the inverse of the product is taken.
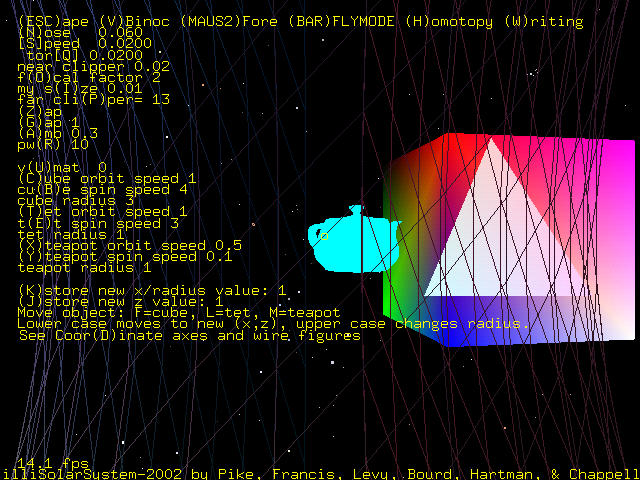
Viewing the arrangement through the torus.
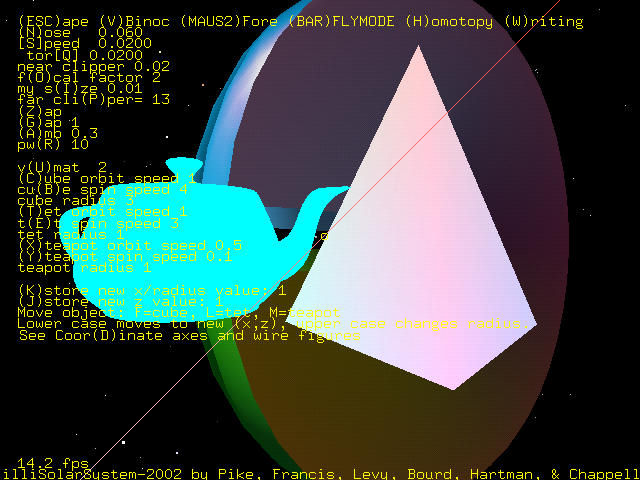
Viewing the arrangement through the cube.
When viewing through an object, the object is drawn in line segments so that the user can see through the object.
The user interface allows one to instantaneously alter the position or radius of an object. See the instructions section for details.
A final feature of this project is being able to see the coordinate axes of each object. With the correct input, all the objects are drawn with line segments and the coordinate axes of each object are displayed. The x-axis is red, the y-axis, green, and the z-axis, blue. There are tic marks on each axis in the positive direction. One of the six directed axes for each object is longer. This allows the coordinate axes to point in the direction that the user will look when viewing through the object.
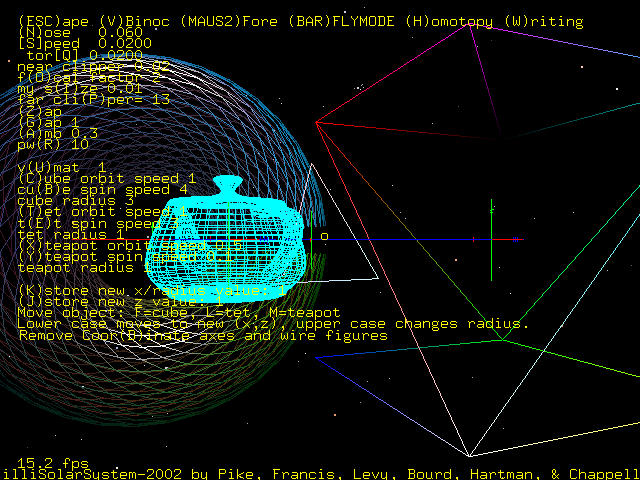
Several additional improvements can be made. First, an improvement could be made so that when viewing through an object, the stars move in the appropriate manner. Also, more objects could be added, and all the objects could be put in elliptical orbits. Perhaps a comet could be added that travels in a hyperbola. This is a creative project, so there are many possibilities for improvements and additions.