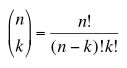
Pascal's triangle has been known to the western world for hundreds of years. It has been modeled countless times in any number of media, and yet it still intrigues the ambitious person who wishes to study it. Combinatorial Pyramids is a tool to study the triangle and its brothers in a three-dimension, computer-animated world. The goal of this world is to easily see the third dimensional version of the triangle, Pascal's tetrahedron. Combinatorial Pyramids also implements the trinomial triangle and its third dimension cousin.
Combinatorial Pyramids was inspired by an earlier project by Lynne Kelly, principal of the Virtual School for the Gifted. She has been working with Pascal's tetrahedron, looking for patterns and interesting phenomena. Her work has been with physical media, however, and the difficulties with building, unbuilding, and computing the next layer of the tetrahedron were very much impeding her study. When I asked her for ideas for a Hypergraphics project, she quickly suggested this. I was interested, and Combinatorial Pyramids was born.
Combinatorial Pyramids is an application written in C using the OpenGL and GLUT libraries. Thus, it is cross-platform and should run on any computer with these libraries available. Developed as a modification of the illiSkel, Combinatorial Pyramids was developed primarily on a Mac running OSX. This necessitated various design changes to the illiSkel code, and I eventually rewrote a good portion of my base.
As stated earlier, Combinatorial Pyramids implements four types of combinatorial paradigms. Pascal's triangle and tetrahedron, as well as the Trinomial version of both are rendered in stunning detail. The user is able to fly through the world and easily visualize the various modes.
Blaise Pascal, who first published his version of the triangle in 1653, described Pascal's triangle in Western mathematics. The nth row of the triangle is equivalent to a binomial expansion of the nth power. Therefore, any specific term of the triangle can be found by
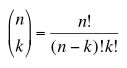
where n is the row and k is the position within the row. This formula is easily implemented in C and so this mode of Combinatorial Pyramids runs quite well. Had I tried to implement this recursively, by adding the two terms above the term I was looking for, it would run very slowly.
Pascal's tetrahedron is an extension of Pascal's triangle into three dimensions. Each of the outside faces of the tetrahedron is Pascal's triangle. Inside numbers are found by adding the three numbers directly below on the level below the term one is looking for. It turns out that when one expands a trinomial (a+b+c)n , the coefficients are levels in Pascal's tetrahedron. Therefore, terms can the tetrahedron can be found by
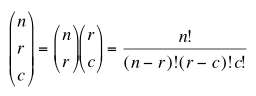
where n is the row, k is the position within the row, and c is the level on which the rows and positions fall. This too is easily implemented in C and so Pascal's tetrahedron can be quickly rendered on the fly.
The trinomial triangle is similar to Pascal's triangle both in that is can be generated recursively, and that its rows give the coefficients to an expansion of terms. This expansion is the expansion of (1+x+x2)n. The trinomial triangle is generated recursively by taking a single one, and below that three more ones, and then adding the number above, above and to the left, and above and to the right in order to produce a term. The outside numbers are ones, just like Pascal's triangle. The first few rows of the trinomial triangle are
1 1 1 1 1 2 3 2 1 1 3 6 7 6 3 1 etc.
I could not find a formula for terms of this triangle, so Combinatorial Pyramids implements the recursive algorithm described above. This is quite slow and no more than ten rows can be drawn before system performance is intolerable.
The trinomial tetrahedron is basically the same as Pascal's tetrahedron, except with a different triangle pattern for the faces. Because the trinomial triangle is implemented recursively, so must the tetrahedral version, and because there are many more terms in the tetrahedron, no more than four or five levels can be drawn with any speed.
Combinatorial Pyramids implements a number of graphical features which illiSkel lacks. Fog rendering adds an enhanced sense of depth to the scene, easing the difficulty of picking out specific patterns in the various modes. Fog can be rendered in three different ways, or completely disabled, depending on the performance of the computer which the application is running on. Combinatorial Pyramids lets the user determine what range of rows the application should compute and render Ð so if one only wants to examine rows six and seven, this is easily accomplished. This is both a computational and visual feature. Rendering and computing fewer rows saves processing time which can be used for other aspects of the application. In addition, it can sometimes be difficult to figure out which points belong to which rows or levels, and disabling rows the user is not examining results in less screen clutter.
Another feature that helps the user determine what he or she is looking at is variable coloration modes. Users of Combinatorial Pyramids can choose from color by row, sequential coloration, or uniform coloration in red, green, blue, yellow, or white. Sequential coloration showed an interesting aspect of the triangles. Because there are five colors, the colors are only stationary if the number of data points is divisible by five. Playing with the number of rows or levels rendered changes this number, resulting in some interesting coloration schemes. Perhaps the best coloration mode is color by row, because this lets the user quickly pick out to which row or level a specific data point belongs.
Because one of the project goals was to get the application running on Mac OSX, much of the navigation system needed to be altered. The one button mouse of the Macintosh works very well for native programs, but not so well for ones developed for three buttons. Therefore, Combinatorial Pyramids was changed to use the primary mouse button to accelerate forwards and backwards. The keyboard function also had to be rewritten, because it was not functioning at all on the Mac. The new function, while much more verbose, is arguably easier to read, and also has the advantage of working on both the Macintosh and on the IRIX machines. Hypothetically, it should work on Windows as well, but Windows support is not a priority and so this has not been tested.
The keyboard and messages functions were both modified to include application-specific functionality. The new messages displayed on-screen can be readily seen. These modifications primarily removed unneeded information and displayed some new information in a low-clutter way. The keyboard modifications simply implemented a number of control functions. The reader should refer to the included ReadMe file for specifics on using Combinatorial Pyramids.
Prior to working on Combinatorial Pyramids, I could read C
code and do some very basic programming. Now I am very comfortable
coding in C in both the IRIX/UNIX environment and on the Mac running
OSX. (This may be in part because OSX is a real BSD UNIX.) I
learned about makefiles on the IRIX boxes and a lot about how OSX
implements libraries (they are called Frameworks, and the OSX IDE,
Project Builder, makes them easier to use than the libraries on the
IRIX machines). I have come to respect the man system. It was a
big help to be able to type "man <function
name>" and have documentation on how to use that function
appear onscreen.
In addition, I learned quite a bit about combinatorics and the math behind the things I visualized. I was somewhat familiar with the binomial theorem and Pascal's triangle before starting the project, but I have learned about expanding trinomials, the special case trinomial which forms the trinomial triangle, and extending both triangles to three dimension. Just figuring out how to display the various functions on-screen was an exercise in mathematics.
This has been an enjoyable project and I hope to continue development. Lynne has just started using the program and I will undoubtedly enjoy detailed feedback from her. Also, I am interested in adding some more features, including dependency tracing, which would show what lower terms a given term is based on, improved navigation, and perhaps other three dimensional shapes besides the triangular based tetrahedron. This may also be an effective CAVE application as well.
Even though mankind has known of Pascal's triangle for hundreds of years, there are still new and interesting things to be done with it. Combinatorial Pyramids is an application implementing some of those things. If the program does nothing but help its users better understand and visualize the topic of combinatorics, it should be considered a success.