
Numerical Simulation of Point Vortex Solutions to Euler's Equation

Early behaviour 20 identical vortices arranged symmetrically along the x-axis
Background
Classical fluids are customarily described in terms of their particle velocities as a funciton of space and time, which obey a very general vector equation called the Navier-Stokes equation. If one makes a great deal of simplifying assumptions, namely that the fluid is inviscid (i.e., does not dissipate energy), incompressible, and two-dimensional, one is left with what is called the two-dimensional Euler equation, which basically equates the rate of change of linear momentum with the pressure gradient.
I will be considering the "vorticity" of the flow, which is the curl of the velocity field. If one takes the curl of both sides of the 2D Euler equation, it happens that points of constant vorticity move about in the flow like material points. Motiviated by this, one can write a solution of the Euler equation that consists of a flow with zero vorticity everywhere except at a finite number of points, where it is described with Dirac delta functions. The resulting equations of motion are governed by a nonlinear system of ODES:
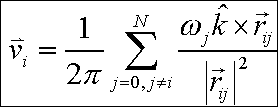
These concentrations of vorticity are called "point vortices", and are, of course, only an approximation to any physical situation. Never the less, they are a useful concept in that they reduce the Euler equation, a continuous differential equation with infinite degrees of freedom, to the motion of the point vortices in their own self-induced flow, which is a system with a finite number of degrees of freedom.
The behaviour of point vortices has shed light on such systems as global weather patterns, superfluid helium, and is a useful tool for computationally estimating the behaviour of continuous fluids (Aref, 1983). In this presentation, however, they will be presented simply as a dynamical system that is interesting in itself.
Numerical Methods
My project is based on numerical methods, not on analytical solutions of point-vortex motion (though of course, some basic analytical understanding is necessary to verify one's results, and makes a correct implementation much more gratifying). Part of the project is, in fact, to demonstrate the relative effectiveness of different numerical methods, themselves.
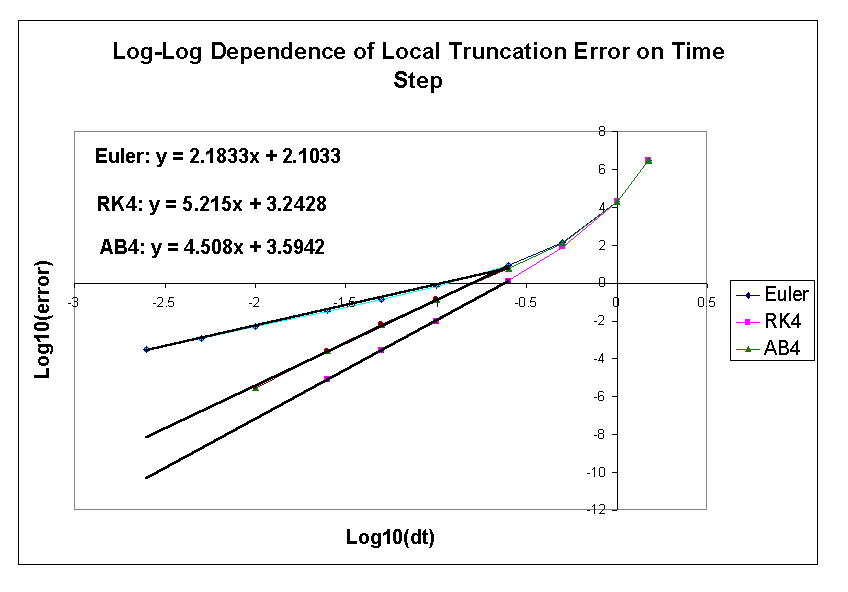
The performance of my schemes demonstrate the expected orders of convergence integrating the exponential function
I have implemented a fourth-order Runge Kutta method, a fourth order Adams-Bashforth method, and for the same of comparison, a simple Euler's method. I will show simultaneous simulations using all three different methods so that one can easily see the relative computational time and accuracy of each technique, discuss methods for estimating errors in numerical calculation, and demonstrate briefly the difficulty of numerically simulating chaotic systems.
More information on numericsTheory
The fun part of the demonstration will be the exhibition of some funky vortex systems, including:
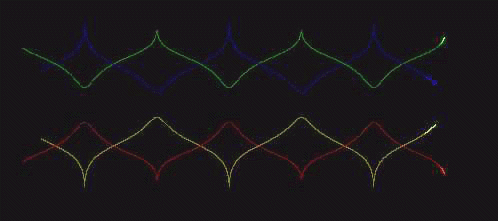
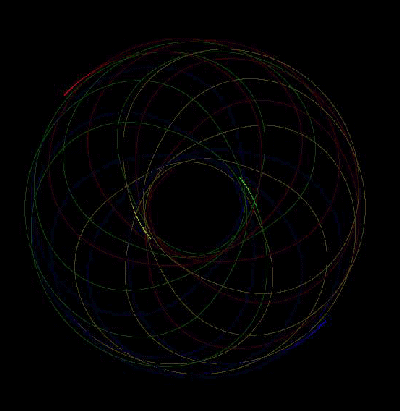

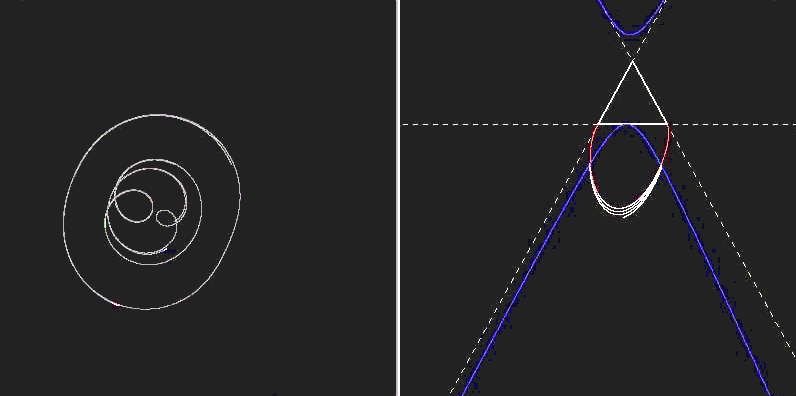
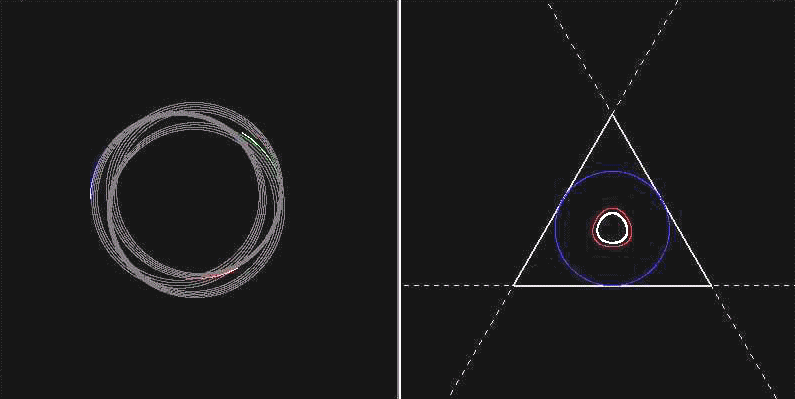
...and possibly more.
The Program(s)
The presentation is based around combination of a number of core routines, all written entirely from scratch. Some of the tasks the program performs are
It should be noted that it would not be hard to adapt this program to plot the behaviour of a wide variety of dynamical systems in various aspects. It would be interesting, for example, to write a program that plotted Poincare sections simultaneously with geometrical coordinates, that had a monitoring window for the numerical variations of "constants" of the motion, that plotted intersection curves of three-dimensional shapes as functions of various parameters, that monitored fourier spectra simultaneously with physical variables, etc. These are all things that I would like to have done, but I didn't have time. Any one would be a great project for a future student.
-Ryan Giordano
rgiordan@uiuc.edu