John Pacey- Summer '08 REU in Mathematics

Feel free to skip ahead to relevant sections by clicking on the appropriate link below

I am a May 2008 graduate of the University of Illinois at Urbana-Champaign. I have a bachelor's degree in Mathematics as well as minors in Computer Science and Secondary Education. I am presently employed as a mathematics teacher at Dixon High School in Dixon, IL. During the spring of 2007 I took Professor George Francis' Math 402 class entitled Non Euclidean Geometry. After learning of my interest in Computer Science and experience programming with Java he asked me to work on a more complete interactive applet demonstrating both Euclidean and Non-Euclidean geometries for use in his Geometry classes. You can learn more about this project here. This work as well as my experience with Mathematica and various programming languages is what led to me being a part of the illiMath2008 REU of Geometrical Visualization in Virtual Environments.

In the pedagogy of an undergraduate course in non-Euclidean geometry, pairwise linked constructions in all models of hyperbolic, elliptic, and Euclidean geometry are desirable. Existant open source and proprietary geometry drawing packages rarely use more than two equivalent models, and almost none link the constructions between pairs of models. This project seeks to remedy this, using a variety of platforms, including Java and Mathematica.

Some of the various geometric drawing programs Professor Francis has utilized in his classes include Geometry Explorer(GEX) and NonEuclid. Professor Francis wanted to be able to combine the plane geometric construction capabilities with side-by-side, linked, non-Euclidean representations of those Euclidean constructions or more generally between any two geometric models. The idea being that students gain a better understanding of Non-Euclidean geometries by viewing them in relation to a geometry (possibly Euclidean) they are familiar with. For example he wanted a student to be able to construct a rectangle in the Euclidean plane and have the ability to view the rectangle in hyperbolic geometry and also have the two models interact with each other. That is, moving the Euclidean rectangle would also move its corresponding representation in hyperbolic geometry and vice versa. While several programs do allow construction in multiple geometries none allowed the user to view a construction in multiple geometries at once.

        Geoproj - Java overview here

Choose the appropriate link below to run each applet: (Java make take quite some time to load initially)

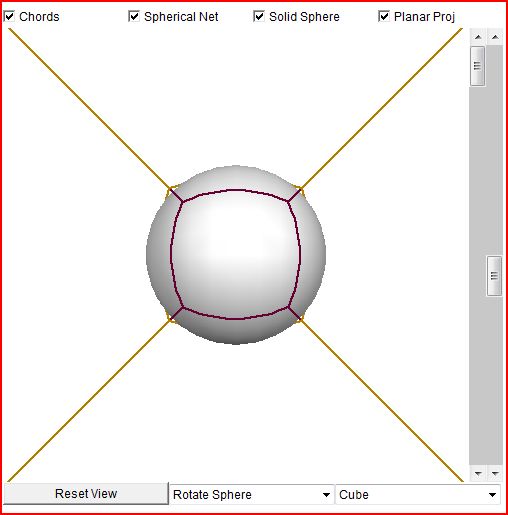
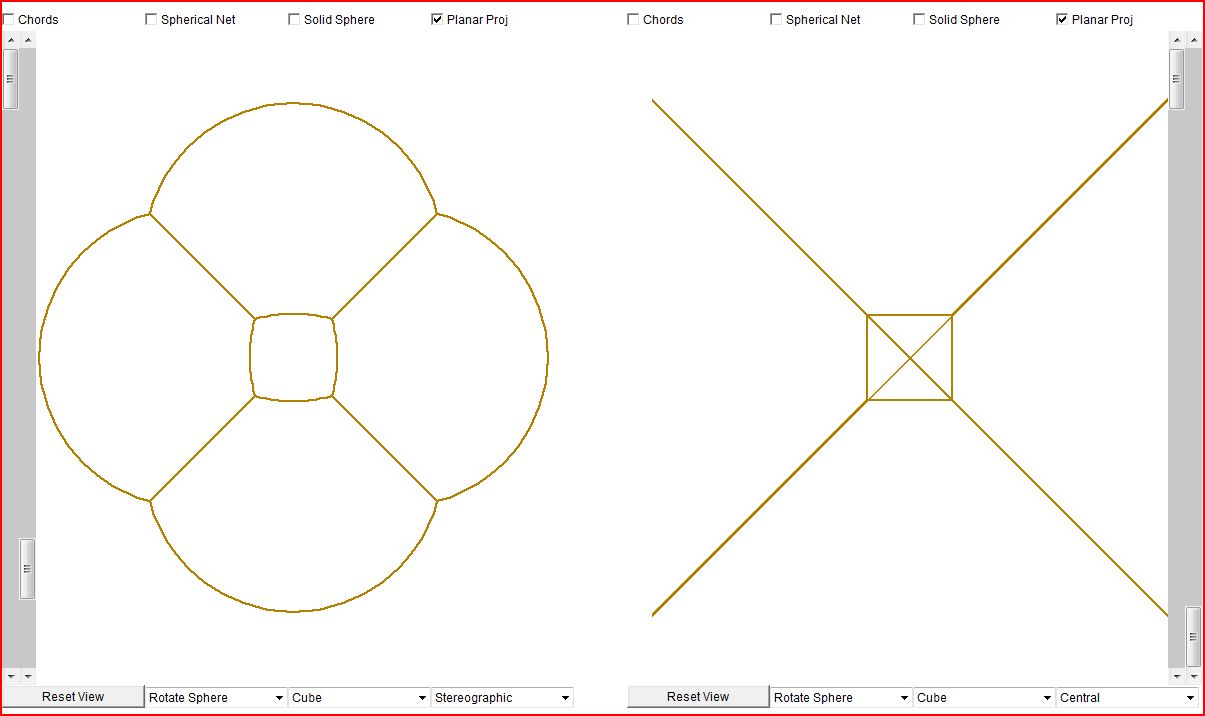
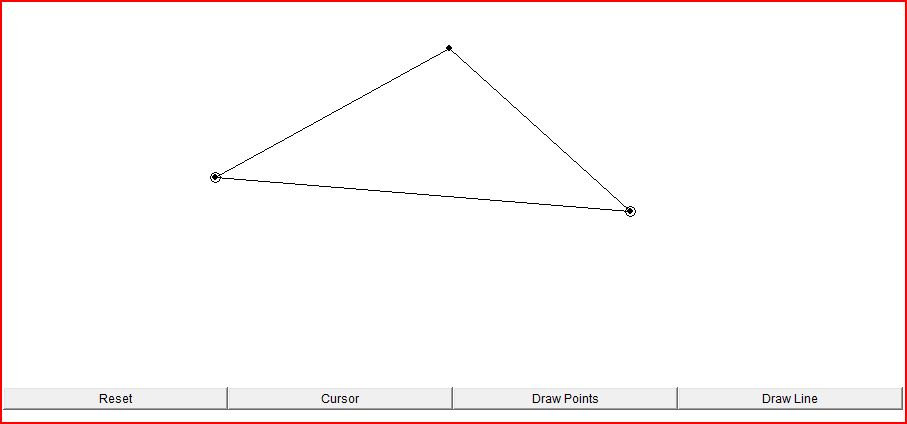
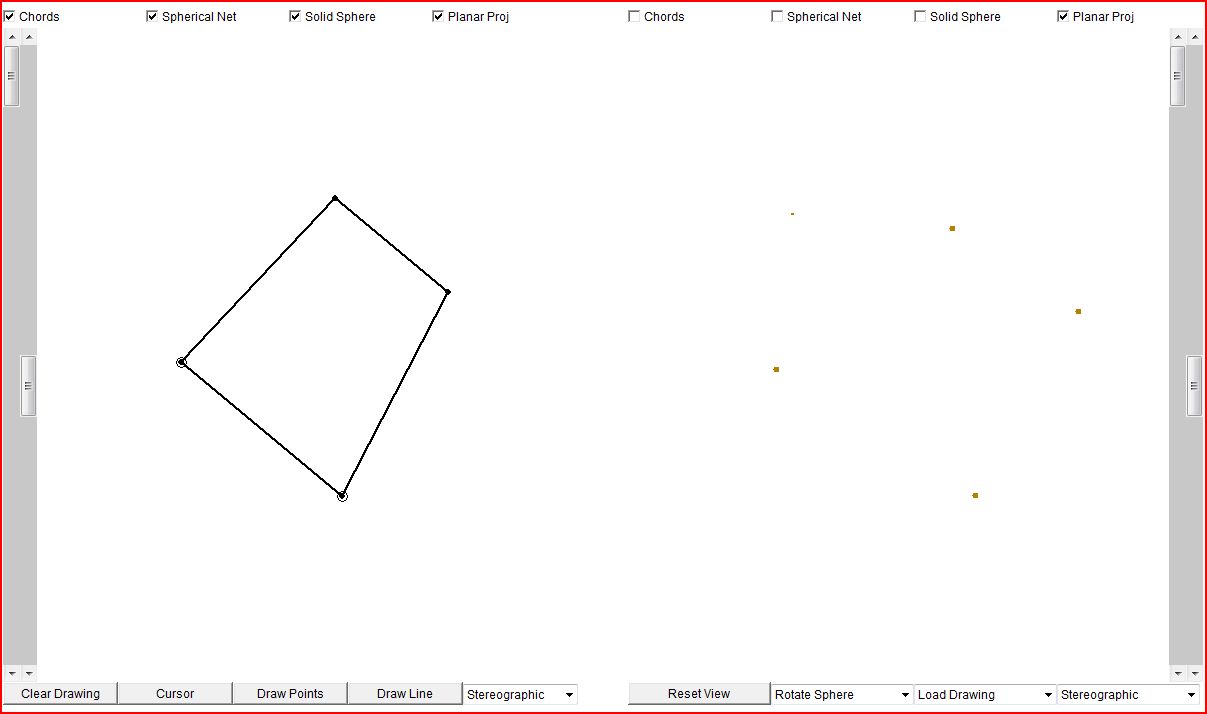
Some images of various versions of GeoProj - Java in action, click for enlarged screenshots:

John Sullivan's site containing the original applet and source code for this project can be found here.

        Geoproj - Mathematica overview here

Some images of various versions of GeoProj - Mathematica in action:

This is an updated version of a project from the second annual workshop in Visual Mathematics: Computer Graphics for the Classroom which took place in the summer of 1992. Below is a description of the original project by Loren Evans. More documentation and a more complete description of the original and subsequent projects is available here.

The goal of this project is to produce an interactive program that allows the user to generate conic sections visually and geometrically as opposed to algebraically, and to view the resultant curves and intersecting surfaces in three dimensions. Allowing real-time interaction with the cutting plane and the generating cones should provide a very concrete visualization of the algebraic concept of a conic section. The opportunity to explore various relationships with this visualization tool should be helpful to anyone interested in quadratic equations and geometric relationships between algebraic entities.

I only translated this program from IRIS GL to OpenGL.  A definitions file i2o.c (should really be i2o.h) is included in the zip file below. Including it in an existing program is meant as a very quick and dirty port of igl programs to opengl but is a good place to start.

Some screenshots of Illiconic in action: