
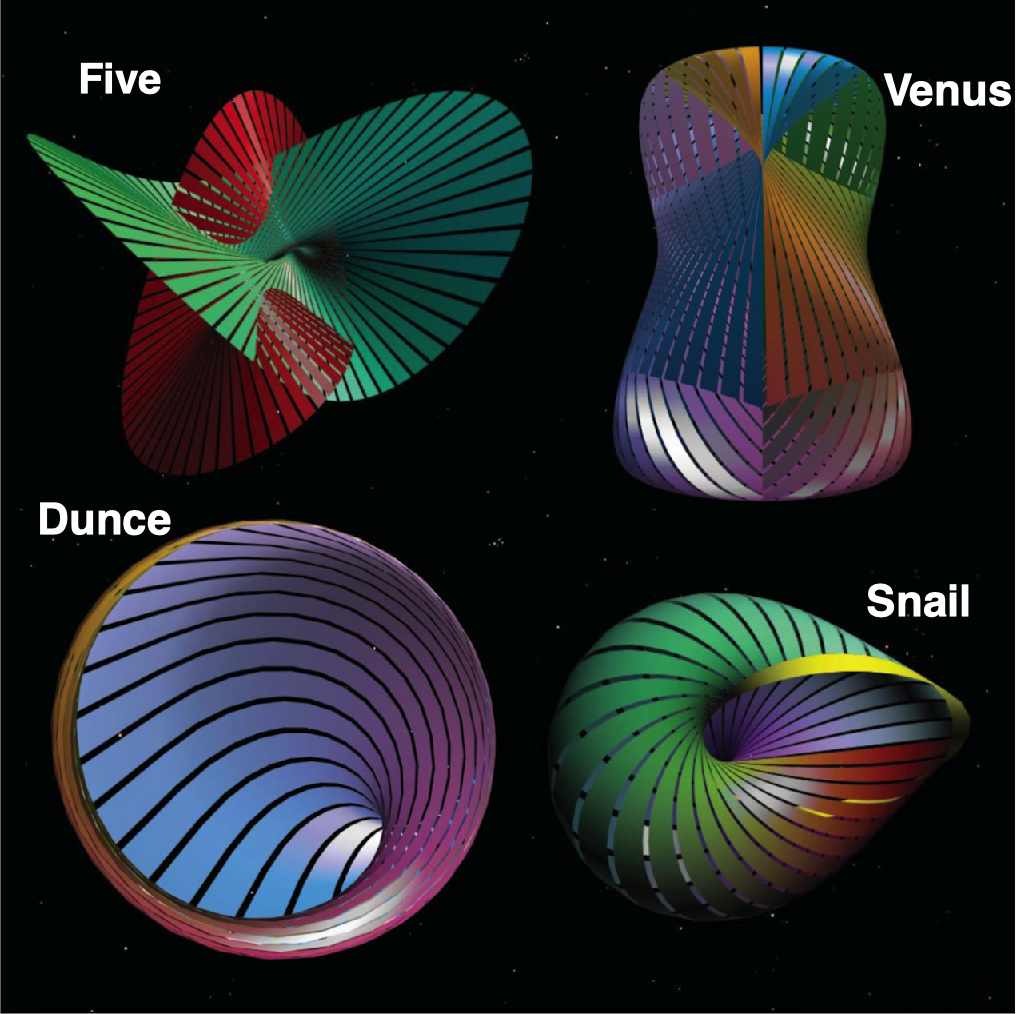


Five Morin-Apery Homotopies "Five"
This immersed cylinder is almost halfway through its eversion. It is the central topological detail in five homotopies, based on the pioneering work on sphere eversion by Bernard Morin. It was originally programmed by Apéry and Chris Hartman in C/IrisGL for the CAVE at the NCSA (1992).
Drawing surfaces and their deformations: The Tobacco Pouch Eversions of the Sphere.
Etruscan Venus and Romboy Homotopy "Venus"
The initial surface is a Whitney-stable 3D projection
of a nonorientable surface with Euler
characteristic 0 (a Kleinbottle) embedded in
4-space. Like Steiner's Roman Surface in François Apéry's
Romboy homotopy, the Etruscan Venus loses its singularities
pairwise and becomes an immersed surface, Ida, which
is the connected sum of two copies of Boy's Surface.
Dalbec Contraction of Zeeman's Duncehat "Dunce"
John Dalbec worked out a contraction of an unusual cell-complex embedded in space, Zeeman’s Duncehat, which is contractable but not collapsible. The surface has one vertex, and a single disk-like sheet attached three times to the one edge.
See also
Dalbec's abstract, Heidelberg, 1993.
Sudanese Moebius Band and Brehm Knotbox "Snail"
A Möbius Band, with a circular edge (yellow) morphs through other bubble-like shapes, until it reaches a ribbon with three half twists whose circular boundary is glued 3-times to the same circle. To the topologist, Ulrich Brehm's Knotbox is a standard spine for the complement of the trefoil knot in the 3-sphere. Think of a bicycle inner tube, but tied in a knot; blow it up until there is no place left in the universe to expand it into. The rubber walls will fuse into a 2-dimensional shape (cell complex) which could look like this from the inside. It is also a stereographic projection of half of Blaine Rolfson's minimal Kleinbottle from the 3-sphere to our Euclidean 3-space.
See also
The Hypergraphics honors seminar at Illinois,
1995-2016.
Page 79 in Diana Davis Editor, Illustrating Mathematics American Mathematical Society, Providence, R.I., 2020