Introduction to the Entire Course
Last updated 12aug12\begin{document} \maketitle
The Warp and Weft of this Course
This course is constructed like a piece of woven cloth, with a warp and weft. The orderly warp of parallel strings represents the progression of three kinds of plane geometry, the affine, projective and transformational. This corresponds to selections from chapter 1, 2 and 4 in Philippe Tondeur's textbook, and chapter 3 of the Topological Picturebook.The weft of the course is a thread that weaves back and forth through the warp. It is organized historically according to the methods typical to each era.
Three Geometries of the Plane
Affine Geometry
In the affine geometry of the plane we subtract something from Eucid's geometry. We do not use the concept of distance and angle. Thus the notion circle and perpendicular does not make sense in affine geometry. But parallel, concurrent, proportions do make sense here. The method we use in our exposition of affine geometry is Cartesian because we use vectors. Thus we initiate the Cartesian thread of the course.
The formative assessment of your mastery of this module is based on your class participation and homework. The summative assessment is an hourly test and the midterm.
Projective Geometry
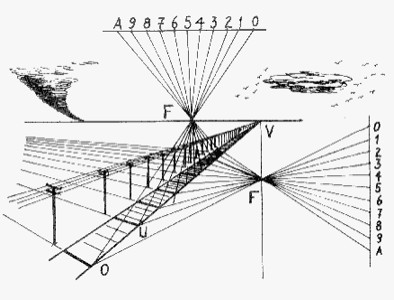
Only twice in our history does art significantly precede mathematics. From the experimental and visual theory of linear perspective derives a projective geometry. In the projective geometry of the plane we change something in Euclid's geometry. We add ideal points and lines, and thereby changing the axioms to make them more "democratic". Just as any two points are joined by a line, now any two lines cross at a point. We give up the concept of parallelism to gain greater generality of our theorems. This material is taken from the author's Topological Picturebook and expanded into lessons on perspective drawings.
Mastery of this second module of the course will be evaluated by the "daily" drawing exercise (formative assessment), and a takehome drawing assignment (summative assessment). A class project on perspective (optional for 3 credit hours, required for 4 credit hours), as proposed by the student and approved by the instructor, completes the this module.
Transformational Geometry
In this module, we study the Euclidean geometry of the plane from the transformational viewpoint, not from the axiomatic viewpoint initiated by Euclid. In his Erlangen Program, Felix Klein established the principle that all geometry derives from the study of transformation groups. We will study transformations that only change the scale relative to a center (dilatations) and those that preserve distance (isometries). Excerpts from Chapter 2 of Tondeur's text and most of Chapter 4 pertain to this module.
This third module of the course will be evaluated by homework and an hourly. A comprehensive final constitutes the summative assessment of the entire course.
Final Examination and Grade
A comprehensive, 3 hour in-class final is the culmination of this course. It can only be taken at the announced time. Do not make arrangements to be absent from the tests or the final. Your course grade reflects my evaluation of your mastery of the course. It does not consist of an accumulation of points. This evaluation is based on many different ways you can demonstrate this mastery. Each contributes a proportion to the grade. A running estimate of your course grade based on accumulated work observed to date can be made on request. But such an estimate has, necessarily, a great margin of error. For instance, every student present the first week of the course is expected to make a B. You can improve this expectation, or fall short of it as the course progresses.
Five Themes in Geometry
The weft of the course is a historical thread of five themes that weaves its way throught he presentation of the course. In your Journal, you should keep track of which theme a particular aspect of a lesson fits into. Some are pretty obvious. Others may lead to an insightful discussion just which theme a particular example illustrates the best. You are weaving your own warp and the weft of the course as we proceed. On the final, you will have the opportunity to write an essay on your success in this endeavor.
The Physical Origins of Greek Geometry
From the dawn of agrarian civilization, in the Nile, Euphrates, Indus valleys, and in China, the earth had to be measured for purposes of ownership, taxation and inheritance of fields. Seasons had to be anticipated, and planting calenders constructed based on astronomical observations. This knowledge was collected by Greek mathematicians, beginning with Thales and Pythagoras 25 centuries ago. It reached its height ca -300 with Euclid's axiomatization of mathematics in his book, The Elements. Archimedes (-200) anticipated the calculus as it applies to physics. It ends with Pappus of Alexandria at about +300.
Renaissance Perspective and 3-dimensional Drawing
Only twice in the history of humanity did art preceed mathematics. In the Renaissance, artists discovered and formalized the rules of linear perspective which only later became projective geometry. Their practices also laid the foundation for non-Euclidean geometry in two senses: with analytical geometry the methods of proof that Euclid enshrined are abandoned. With transformational geometry the Euclid's postulates themselves are altered or denied.
The Industrial Origins of Cartesian Geometry
In the 17th century, Descartes and Fermat created what we now call analytical geometry. Instead of the axiomatic method of the Greeks, Cartesian geometry is based on the properties of numbers, and uses algebra as its main method of discovery and proof. The contemporary form of this is vector geometry. It was further developed by Newton and Leibniz for their invention of the Calculus. Thus, Cartesian geometry is the foundation of all present day science and technology.
Klein’s Erlangen Program to Unify Geometry
In the 19th century, the problem of making geometry, and mathematics in general, a logically rigorous science was take up in earnest. At the beginning of the century, the philosopher Emmanuel Kant still taught that the geometry of Euclid is the only kind of geometry that there is because any other kind is inconceivable by the human mind. By the end of the century, mathematicians had shown that many geometries which violated Euclid's axioms, not only "were conceivable to the human mind" but that they were equi-consistent with Euclidean geometry. In particular, if these non-Euclidean geometries were inconsistent, so is Euclid's geometry, and all of the rest of mathematics. This story is treated in Math 402 "Post-Euclidean Geometry", the sister course to this one.
Felix Klein proposes that the various kinds of geometry could be based on their groups of isometries. That is, the collection of transformations which preserves the properties of interest in a particular geometry, can be considered the foundation of that geometry. This approach replaces the axiomatic method of the Greeks. As we shall see in the last part of the course, a precise definition of how to measure the distance between two points suffices for building up the entire edifice of plane geometry.
The Geometry in Computer Graphics
In the last decades of the 20th century, the artistic and technological demands of computer graphics has led to corresponding changes in mathematical teaching and research, much as perspective did in the Renaissance. This course, MA403, is increasingly a witness to this evolution as it pertains to college geometry.