Constructing a Three-Point Perspective Peeping House

by Jason Mead

Math 403 Project Fall 2006

©Board of Trustees University of Illinois

 

The goal of this assignment is to construct the exact viewpoint from where your three-point perspective drawing will appear to be exactly accurate from a Euclidean distance point of view.

 

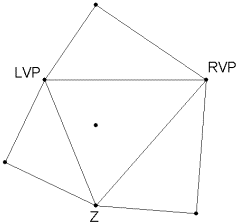
1. Construct a triangle with your three vanishing points (left vanishing point, right vanishing point, and zenith). Then, copy this triangle exactly onto cardboard or a sheet of paper.

 

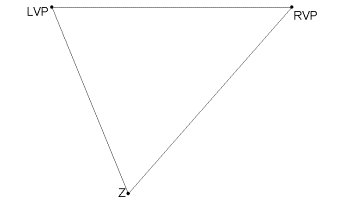
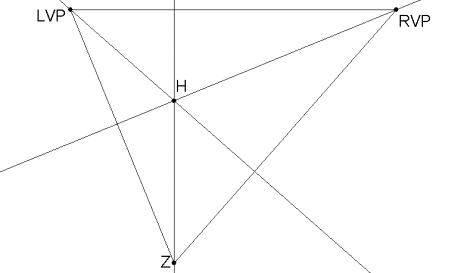
2. Using the copy, construct the altitudes of the triangle, which should meet at H. H is the projection of the viewpoint onto the drawing plane.

 

3. Find the midpoints of each of the sides of your triangle and construct three semicircles, one with each of the sides of the triangle as a diameter.

 

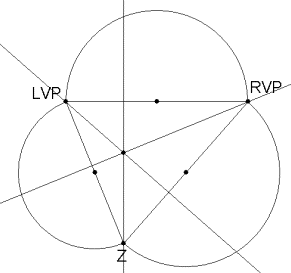
4. Find the points of intersection of the altitudes with their corresponding semicircle.

 

 

 

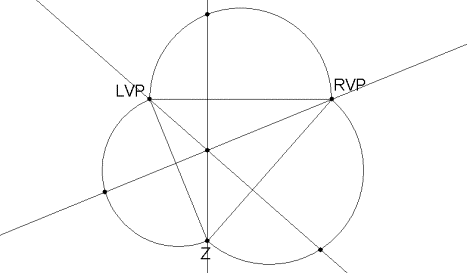
5. Construct Thales right triangles in each of the semicircles containing the two endpoints of the diameter and the intersection point of the altitude with the semicircle.

 

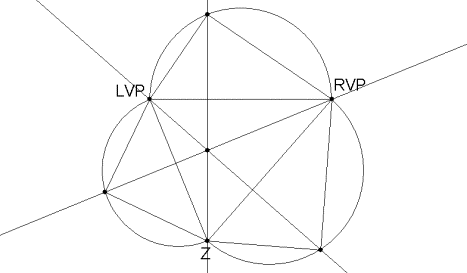
All necessary components of your peeping house have been constructed. To complete the project, cut the six-sided figure out from the rest of your paper/cardboard and fold the edges along the sides of the triangle until the peaks meet at the viewpoint H. Then, tape the edges to keep your peeping house upright.

 

 

 

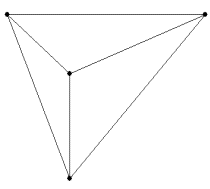
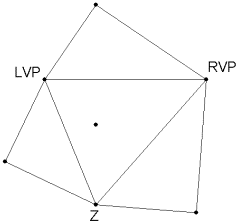
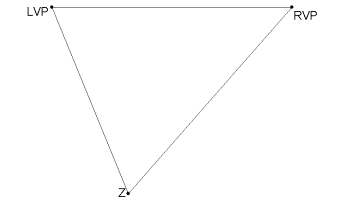
Before folding                                                                After folding

It is worth noting that, many times, someone constructing a peeping house wants to make a larger peeping house than would be possible by using a compass. This would make the eye level significantly higher than possible without a compass. So, while the geometry of the above tutorial is correct, there are reasons to stray from using a compass.

 

To do that, follow the steps below.

 

1. Same as above.

 

2. Same as above.

 

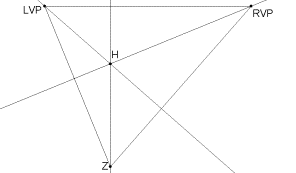3.  Slide a right angle along each of the altitudes outside triangle until you find the point on the altitude that has the edges of your right angle meeting the corresponding corners of the original triangle. You will likely have to twist your right angle as you move it along the altitude. Common right angles might be the edge of a piece of paper, poster board, or a right-angled ruler.

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Construct the Thales right triangles from the points on the altitudes to the edges of the original triangle.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Constructing a Three-Point Perspective Cube

 

The goal of this assignment is to construct a three-point perspective cube drawing that will appear to be exactly accurate from a Euclidean distance point of view from your peeping house.

 

Now that you have completed a peeping house, actually constructing a perspective cube—one of the main ideas of drawing in perspective—will become more easily visible from the exact eye level necessary. But, it is important to know how to construct a perspective cube in order to be able to look at it!

 

1. Use the original triangle from your peeping house, or an exact replica.

 

 

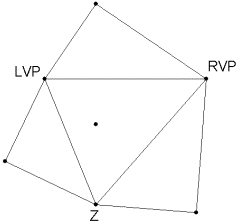2. By the same constructive method as the peeping house, construct Thales right triangles along each edge.

 

3. Bisect the right angles on each of the Thales right triangles and find the point where the angle bisector meets the corresponding edge of the triangle. Each of these meeting places is a Òdiagonal vanishing point.Ó

 

 

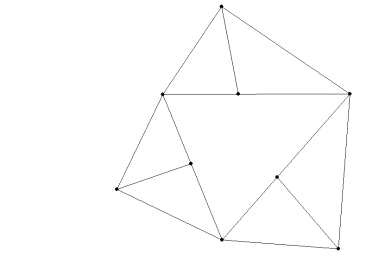
4. You now have all necessary components to begin sketching a cube. First, we will construct a cube on the inside of your triangle. Although this is not going to be visible when you place the peeping house over your base triangle, it is an important skill for your future perspective drawing assignments.

 

Draw a line segment of any length (although the larger your line segment is, the more unwieldy your cube may become) that has an extended line connecting to a vertex of your triangle.

 


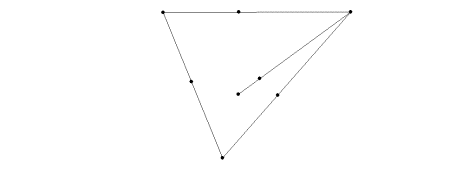
5. Connect the two endpoints of the line segment to another vertex of your triangle.

 

 

 

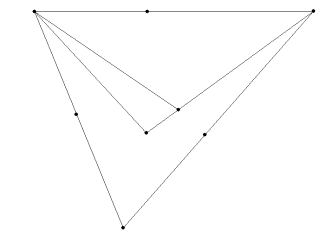
6. Connect the diagonal vanishing point between the two vertices you are using with a point on the original line segment so that your newly constructed line crosses over one of the lines drawn in step 5.

 

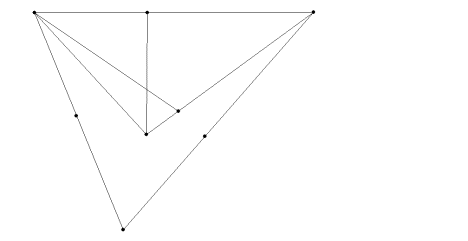
7. Connect the new intersection with the first vertex you used to create a final line segment. This is a perspective square—all the line segments in your perspective square have equal perspective distance (almost certainly not equal Euclidean distance, though).

 

 

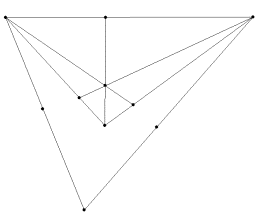
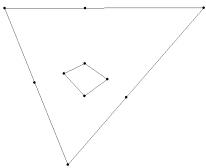
8. To make a cube, draw lines from the endpoints of one of the segments to the final vertex (or zenith).

 

 

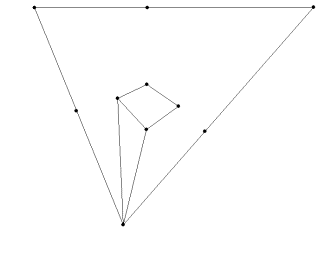
9. Use the diagonal vanishing point between the vertices that you are currently using (in our picture, the original line segment vanishes at the LVP and the other lines will vanish at Z) to perform the same construction as in step 6.

 

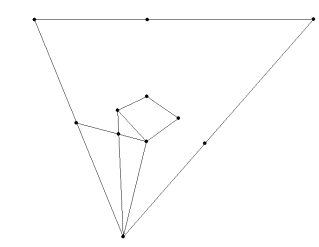
10. Connect the final line segment of your second square from the vertex of the original triangle that the line segment you started with for this square.

 

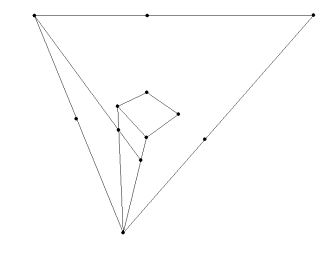
11. To complete the cube, simply draw the final lines as seen in the picture below.

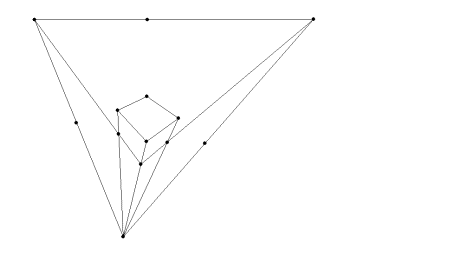
Connecting the final two lines gives another intersection point. To check if you drew the cube correctly, make sure all of the line segments in your cube extend to meet at a vanishing point (NOT a diagonal vanishing point—the diagonal vanishing points [DVPs] are only used to find the lengths necessary for an accurate cube, not to have cube lines that connect to them).

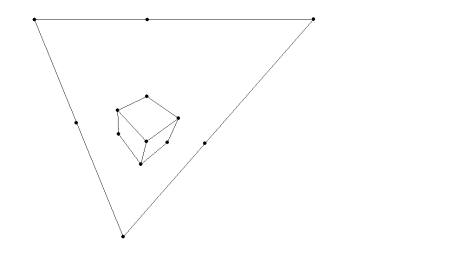
The exact same steps are applied to construct a perspective cube outside the triangle. The benefit of constructing a perspective cube outside the triangle is that you can see, visually, that the viewpoint from the peeping house makes the perspective cube look like a Euclidean cube.

 

a)

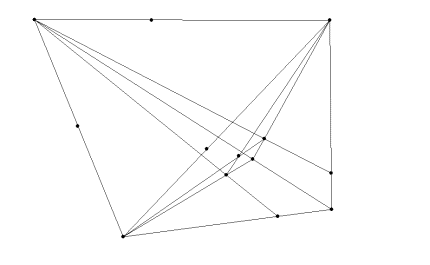
b)                                                                            c)

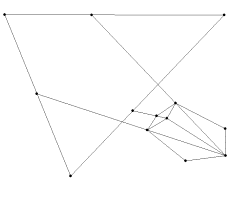
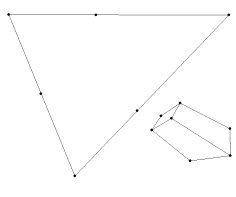
The above pictures are a) a perspective cube outside the triangle with the vanishing construction lines to the vertices still in tact, b) the same perspective cube with the DVP construction lines, and c) the perspective cube with no construction lines.

 

In order to view this cube with Euclidean distance qualities, place your peeping house exactly over the original triangle and look from the viewpoint toward the perspective cube.

 

Bibliography

 

Baran, Ilya. KSEG. Version 0.403. Massachusetts Institute of Technology. Updated February 3, 2006. Available at http://www.mit.edu/~ibaran/kseg.html

Francis, George. ÒPictures in Perspective.Ó Chapter 3 of A Topological Picturebook. Springer Paperback, 2006.