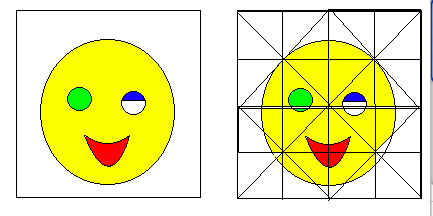
Albrecht Duerer drew a version of the the following in his books instructing the art of perspective drawing. Consider a yellow Smiley Face with a green eye, and a red grin. To
|
An orthographic grid is superimposed on a given figure.. |
help the artist sketch Smiley in perspective. A square surrounding the figure is subdivided several times by first finding the midpoint of a square by crossing diagonals. Then drawing lines parallel to the sides.
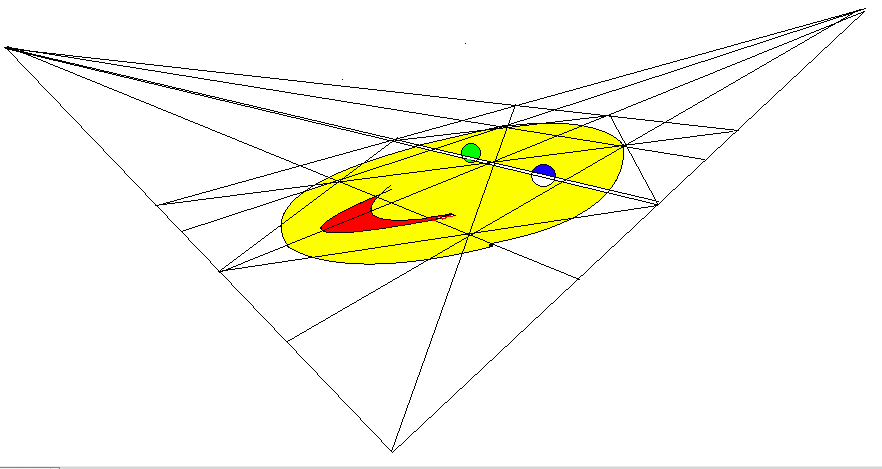
To transfer this into perspective we start with a perspective square. Connecting corresponding pairs of points in the orthographic figure and in the perspective figure produces the line in perspective. Two lines cross at the point in perspecive, that their orthographics counterparts do. To draw parallels in perspective is even easier than orthographically because we connect vanishing points to midpoints of the squares.
|
The same figure is drawn in perspective, using the grid as an aid. |
We now use the grid in perspective to locate places for the lines in the orthographics picture. The figures drawn here were not done in freehand, which would have been much easier. They were done in iPaint, in which curves are a bit tricky to do. Fortunately, iPaint has a zoom feature that allows you apply pixel level detail. A bonus is an easy way of coloring corresponding regions to help identifying correspondences.
You may note that Albrecht Duerer’s picture for how to use Alberti’s Veil for perspective drawing discussed earlier is an example of this process.