Lab on Perspective Boxes
28oct11\begin{document} \maketitle Earlier, we determined that it would be nice to have the same cube appear in all three perspectives (right) so that corresponding elements of its perspective frame can be compared.
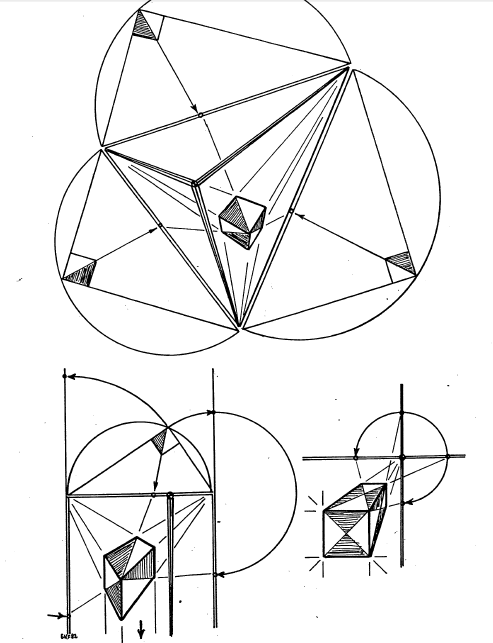 \section{Introduction}
In this lab we reverted to a paper, pencil and gnomon solution to measuring
two boxes, the second of which crosses the horizon. The gnomon in this case
was a file card. All circular arcs needed were supplied as part of the
given figure.
\subsection{Measure the box below the horizon}
\section{Introduction}
In this lab we reverted to a paper, pencil and gnomon solution to measuring
two boxes, the second of which crosses the horizon. The gnomon in this case
was a file card. All circular arcs needed were supplied as part of the
given figure.
\subsection{Measure the box below the horizon}
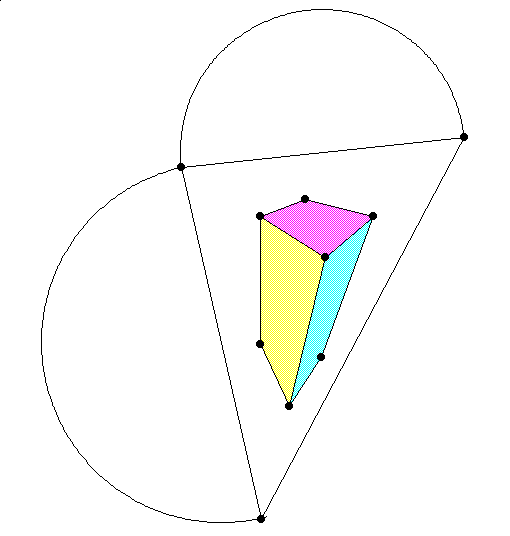 Many in the class had trouble finding the perspective frame for this figure.
Review perspective framings, location of Thales triangles, eye point etc.
Many in the class started by putting in a grid of squares into the Thales
triangles. This is inefficient until after you have found the lines to the
diagonal points whose "slope" you're trying to measure. Review the relation
between the diagonal lines and the proportions of the orthographic
rectangles they diagonalize.
Finally, the mystery of what to do with two rectangles, their proportions
and a common side. If one face of the box comes out in the ratio of
7:2 for example, and the other comes out in the ration of 5:3, AND
the common side is the "2" in the first, but the "3" in the second, then
the common factore is 6=2*3, and the common proportion is 21:6:10.
Many in the class had trouble finding the perspective frame for this figure.
Review perspective framings, location of Thales triangles, eye point etc.
Many in the class started by putting in a grid of squares into the Thales
triangles. This is inefficient until after you have found the lines to the
diagonal points whose "slope" you're trying to measure. Review the relation
between the diagonal lines and the proportions of the orthographic
rectangles they diagonalize.
Finally, the mystery of what to do with two rectangles, their proportions
and a common side. If one face of the box comes out in the ratio of
7:2 for example, and the other comes out in the ration of 5:3, AND
the common side is the "2" in the first, but the "3" in the second, then
the common factore is 6=2*3, and the common proportion is 21:6:10.
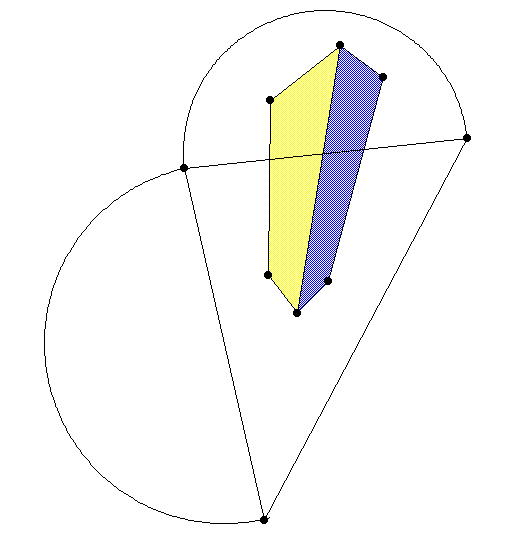 \subsection{Measure the box crossing the horizon}
Do the "same" as before, but with some extra ingenuity. In addition,
you should use a perspective ruler to estimate from what level you're
looking at the "building". Since you're measuring a vertical lenghth,
and verticals vanish at the zenith, you'll need a ruler adapted to
that vanishing point. Since no dimensions in feet are given, you can
only estimate the ratio of the height relative to the height of the
"building".
\end{document}
\subsection{Measure the box crossing the horizon}
Do the "same" as before, but with some extra ingenuity. In addition,
you should use a perspective ruler to estimate from what level you're
looking at the "building". Since you're measuring a vertical lenghth,
and verticals vanish at the zenith, you'll need a ruler adapted to
that vanishing point. Since no dimensions in feet are given, you can
only estimate the ratio of the height relative to the height of the
"building".
\end{document}