Exercise on Ideal Desargues Figures
28jun10\begin{document} \maketitle
 \section{Introduction}
To appreciate what you learned in lesson P1 on Kepler's extended plane,
it is instructive to continue the lesson, A9, on Desargue's Theorem,
by drawing Desargue's figure when some of the given points are ideal.
\subsection{KSEG experiments}
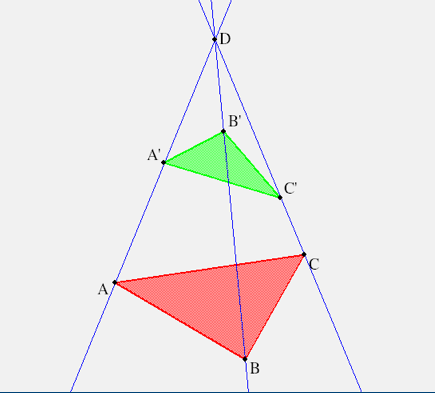
You can use KSEG here is two ways. For the first, draw the standard
Desargues figure, where all given points are in the finite plane. Then
distort the picture, by pushing one points, for example $D$, further and
further away from the other points. The three lines $(AA'), (BB'), (CC')$
will approach being parallel. The second method is to "go to the limit".
Thus $D$ is ideal means that the three lines are given to be parallel
in the Euclidean plane. Show experimentally that Desargues' theorem still
holds in this case, by choosing the points $A,A',B,B',C,C'$ on the three
parallel lines, but then constructing the points $A^*=(BC)(B'C')$ etc, and
showing that these three points, $(A^* B^* C^*)$ are collinear.
\section{Exercise: D is ideal}
Submit a .seg file of Desargues' figure when $D=(AA')(BB')(CC')$ is ideal.
\subsection{Hint}
An outline of the solution was already given above.
\section{Exercise: A is ideal}
Submit a .seg file of Desargues' figure when $A$ is ideal
\subsection{Hint}
This one you need to think about carefully. For $A$ to be ideal,
the two lines $(AC)$ and $(AB)$ have to be parallel in the Euclidean
plane. What about the line $(AA')$ ? Since this line also passes through
the same ideal point $A$ it must be parallel to the other two line through
$A$.
\end{document}
\section{Introduction}
To appreciate what you learned in lesson P1 on Kepler's extended plane,
it is instructive to continue the lesson, A9, on Desargue's Theorem,
by drawing Desargue's figure when some of the given points are ideal.
\subsection{KSEG experiments}
You can use KSEG here is two ways. For the first, draw the standard
Desargues figure, where all given points are in the finite plane. Then
distort the picture, by pushing one points, for example $D$, further and
further away from the other points. The three lines $(AA'), (BB'), (CC')$
will approach being parallel. The second method is to "go to the limit".
Thus $D$ is ideal means that the three lines are given to be parallel
in the Euclidean plane. Show experimentally that Desargues' theorem still
holds in this case, by choosing the points $A,A',B,B',C,C'$ on the three
parallel lines, but then constructing the points $A^*=(BC)(B'C')$ etc, and
showing that these three points, $(A^* B^* C^*)$ are collinear.
\section{Exercise: D is ideal}
Submit a .seg file of Desargues' figure when $D=(AA')(BB')(CC')$ is ideal.
\subsection{Hint}
An outline of the solution was already given above.
\section{Exercise: A is ideal}
Submit a .seg file of Desargues' figure when $A$ is ideal
\subsection{Hint}
This one you need to think about carefully. For $A$ to be ideal,
the two lines $(AC)$ and $(AB)$ have to be parallel in the Euclidean
plane. What about the line $(AA')$ ? Since this line also passes through
the same ideal point $A$ it must be parallel to the other two line through
$A$.
\end{document}