Cube in Two Point Perspective
4jul10\begin{document} \maketitle
 \section{Introduction}
This exercise combines several previous exercises. Recall that in the
exercise to determine from where an arbitrary convex quadrilateral looks
like a square, there was a special solution in which the eypoint is choses
on the horizon. It is where the altitude of the Thales triangle crosses
the horizon, and it corresponds to the special case that the artist's
canvas is vertical. We can treat this as a truly exceptional case, which
is in many respects easier to draw in. For artists, this would be the
proper choice.
For mathematicians, it is a limiting case, when the zenith point
to the horizon escapes to infinity. That is, the triangle of the
perspective frame has one ideal vertex.
Of course, the concept of the eye point as the orthocenter of the
perspective triangle no longer makes sense, because there no altitudes
to be concurrent. But that's OK because you have already chosen the
eyepoint $Ep$.
In addition there is only one Thales $\triangle(T\ Lvp\ Rvp)$ to use for
the horizontal diagonal vanishing point $Dvp$. As explained in the notes,
the other two diagonal vanishing points are very easy to find. The distance
$Lvp$ to $T$ is the same as the distance $Lvp$ to $Ldp$.
\section{Exercise}
Given an arbitrary convex quadrilateral, complete it to a cube in 2 point
perspective.
\subsection{KSEG}
This exercise is to be done in KSEG, because accuracy and wiggling are
instructive. The figure at the right was done freehand in iPaint. It might
correspond to something you'd draw freehand with a pencil and ruler on an
exam. But it suffices to see what need to do.
\subsection{Hint}
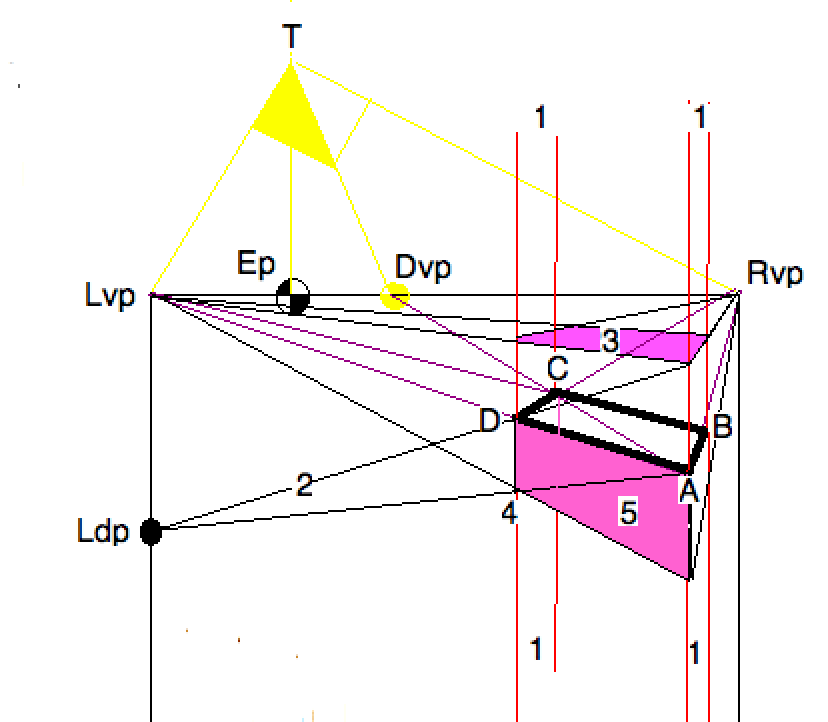
So, given convex quadrilateral $ABCD$, the perspective frame with its
vanishing points are found. This determines the horizontal Thales triangle
(yellow). Since this drawing is to be in 2pt perspective, we know that the vertical sides
(step 1)
of the cube are on the vertical lines (red). The question is how far up or
down. For up, use (2) the left diagonal vanishing point $Ldp$ to find the
corner above $A$, and complete (3) the top (purple) of a cube above the
given base. To build down, use the diagonal (4) from $A$ instead of $D$ to
complete the left vertical wall (5) of the cube building down.
\section{Discussion}
We have actually build two cubes, one up, another down, from the given
base square. You need only do one, but wiggle it above and below the horizon
to see what happens. Whether to use two-point or three-point (or even
one-point) perspective for a drawing depends on many artistic factors.
Two point is faster. But, in drawing a tall building for example, 2pt
perspective looks awkward. Remember that the eypoint is at the level of the
horizon. We rarely lie on the ground when regarding a sky scraper. Indeed,
it looks better to take a birds-eye view. In that cave the camera is well
above the horizon. Perhaps you're in a helicopter. This picture will be in 3pt
perspective.
How can we tell? Well, in 2pt perspective four of the edges of a cube, or a
box for that matter, will be parallel to the canvas. So, when that is not
the case, the box is in 3pt perspective.
\end{document}
\section{Introduction}
This exercise combines several previous exercises. Recall that in the
exercise to determine from where an arbitrary convex quadrilateral looks
like a square, there was a special solution in which the eypoint is choses
on the horizon. It is where the altitude of the Thales triangle crosses
the horizon, and it corresponds to the special case that the artist's
canvas is vertical. We can treat this as a truly exceptional case, which
is in many respects easier to draw in. For artists, this would be the
proper choice.
For mathematicians, it is a limiting case, when the zenith point
to the horizon escapes to infinity. That is, the triangle of the
perspective frame has one ideal vertex.
Of course, the concept of the eye point as the orthocenter of the
perspective triangle no longer makes sense, because there no altitudes
to be concurrent. But that's OK because you have already chosen the
eyepoint $Ep$.
In addition there is only one Thales $\triangle(T\ Lvp\ Rvp)$ to use for
the horizontal diagonal vanishing point $Dvp$. As explained in the notes,
the other two diagonal vanishing points are very easy to find. The distance
$Lvp$ to $T$ is the same as the distance $Lvp$ to $Ldp$.
\section{Exercise}
Given an arbitrary convex quadrilateral, complete it to a cube in 2 point
perspective.
\subsection{KSEG}
This exercise is to be done in KSEG, because accuracy and wiggling are
instructive. The figure at the right was done freehand in iPaint. It might
correspond to something you'd draw freehand with a pencil and ruler on an
exam. But it suffices to see what need to do.
\subsection{Hint}
So, given convex quadrilateral $ABCD$, the perspective frame with its
vanishing points are found. This determines the horizontal Thales triangle
(yellow). Since this drawing is to be in 2pt perspective, we know that the vertical sides
(step 1)
of the cube are on the vertical lines (red). The question is how far up or
down. For up, use (2) the left diagonal vanishing point $Ldp$ to find the
corner above $A$, and complete (3) the top (purple) of a cube above the
given base. To build down, use the diagonal (4) from $A$ instead of $D$ to
complete the left vertical wall (5) of the cube building down.
\section{Discussion}
We have actually build two cubes, one up, another down, from the given
base square. You need only do one, but wiggle it above and below the horizon
to see what happens. Whether to use two-point or three-point (or even
one-point) perspective for a drawing depends on many artistic factors.
Two point is faster. But, in drawing a tall building for example, 2pt
perspective looks awkward. Remember that the eypoint is at the level of the
horizon. We rarely lie on the ground when regarding a sky scraper. Indeed,
it looks better to take a birds-eye view. In that cave the camera is well
above the horizon. Perhaps you're in a helicopter. This picture will be in 3pt
perspective.
How can we tell? Well, in 2pt perspective four of the edges of a cube, or a
box for that matter, will be parallel to the canvas. So, when that is not
the case, the box is in 3pt perspective.
\end{document}