Lesson: M9
==========

The Law of Sines
----------------

.Definition.
*************
sin asciimath:[alpha=frac{text{secant}}{text{diameter}}].
*************

For this definition to make sense, we need the

.Peripheral Angle Theorem.
****************
Two peripheral angles subtending the same secant of a circle are equal or supplementary and therefore have the same sine.
****************

'Proof.' Let asciimath:[A] be the center of a circle. First we consider the case where one side is a diameter. Let asciimath:[DB] be a diameter. Then for a point asciimath:[C] on the circle, asciimath:[/_BAC] is an exterior angle of the isoceles △asciimath:[DAC].

[frame="none",cols="^",valign="middle",grid="all"]
|===================
|pass:[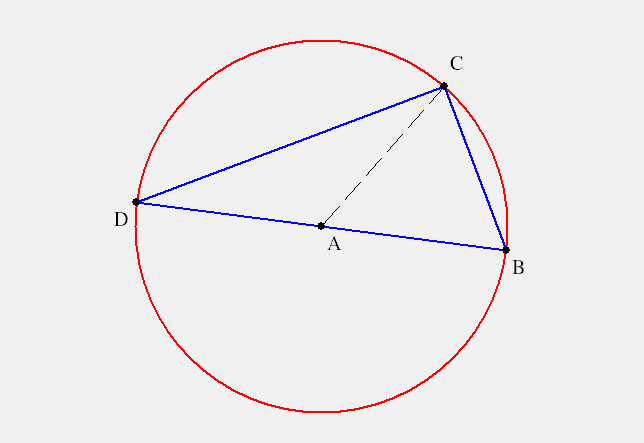<A href="403m9-1.seg"><IMG src="403m9-1.png" alt="403m9-1.png"></A>]
|*Click image to view in KSEG.*
|
|===================

By the Exterior Angle Theorem of Euclid, we have

[frame="none",cols="^",valign="middle",grid="none"]
|===================
|asciimath:[/_BAC=/_ADC+/_DCA=alpha+alpha=2 alpha].
|===================

So the peripheral angle is half the central angle to the same secant asciimath:[CB]. 

Recall the Law of Sines from trigonometry:

.Law of Sines.
****************
[frame="none",cols="^",valign="middle",grid="none"]
|===================
|asciimath:[frac{sin\ alpha}{a}=frac{sin\ beta}{b}=frac{sin\ gamma}{c}].
|===================
****************

The Cross Ratio
---------------

.Definition.
*************
Given four collinear points asciimath:[ABCD] (in any order), the 'cross ratio' asciimath:[CR(ABCD)] is

[frame="none",cols=">,^,>",valign="middle",grid="none"]
|===================
||asciimath:[frac{A-B}{A-D}\ frac{C-D}{C-B}\ =\ frac{sin/_BPA}{sin/_DPA}\ frac{sin/_DPC}{sin/_BPC}]|asciimath:[(**)],
|===================

where asciimath:[P] is any point not on the line.
*************

[frame="none",cols="^",valign="middle",grid="all"]
|===================
|pass:[<A href="403m9-2.seg"><IMG src="403m9-2.png" alt="403m9-2.png"></A>]
|*Click image to view in KSEG.*
|
|===================

'Proof of asciimath:[(**)].' Apply the Law of Sines to &#x025B3;asciimath:[ABP] then

[frame="none",cols="^",valign="middle",grid="none"]
|===================
|asciimath:[frac{A-B}{sin/_BPA}=frac{a}{sin/_B}=frac{b}{sin/_A}],
|===================

where asciimath:[A-B] is the signed length asciimath:[|A-B|] and asciimath:[sin/_B=sin/_PBA=sin/_CBP] since supplementary angles have the same sine. Now let's calculate

[frame="none",cols="^",valign="middle",grid="none"]
|===================
|asciimath:[frac{A-B}{A-D}\ frac{C-D}{C-B}\ =\ frac{A-B}{sin/_BPA}\ frac{C-D}{sin/_DPC}\ =\ frac{P-A}{sin/_B}\ frac{P-C}{sin/_D}].
|===================

Similarly,

[frame="none",cols="^",valign="middle",grid="none"]
|===================
|asciimath:[frac{sin/_BPA}{sin/_DPA}\ frac{sin/_DPC}{sin/_BPC}\ =\ frac{A-D}{sin/_DPA}\ frac{C-B}{sin/_BPC}\ =\ frac{P-A}{sin/_D}\ frac{P-C}{sin/_B}].
|===================

So asciimath:[frac{A-B}{A-D}\ frac{C-D}{C-B}\ =\ frac{sin/_BPA}{sin/_DPA}\ frac{sin/_DPC}{sin/_BPC}\ \ square].

Perspective Rulers
------------------

.Definition.
*************
A 'ruler' is a line together with a copy of the real numbers on it.
*************

A 'perspective ruler' on a line with a finite vanishing point is obtained with the following procedure: given asciimath:[l] with vanishing point asciimath:[V],

- Choose a  point asciimath:[P] not on asciimath:[l] on the extension of asciimath:[l] past asciimath:[V].
- Choose a line asciimath:[s\ ||\ (PV)].
- On asciimath:[s] choose a Euclidean ruler.
- Transfer this scale through the lens asciimath:[P] to asciimath:[l].

[frame="none",cols="^",valign="middle",grid="all"]
|===================
|pass:[<A href="persruler.seg"><IMG src="persruler.png" alt="persruler.png"></A>]
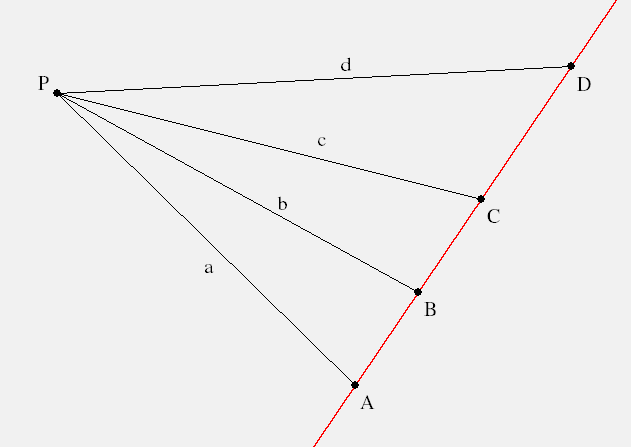|*Click image to view in KSEG.*
|
|===================