For this definition to make sense, we need the
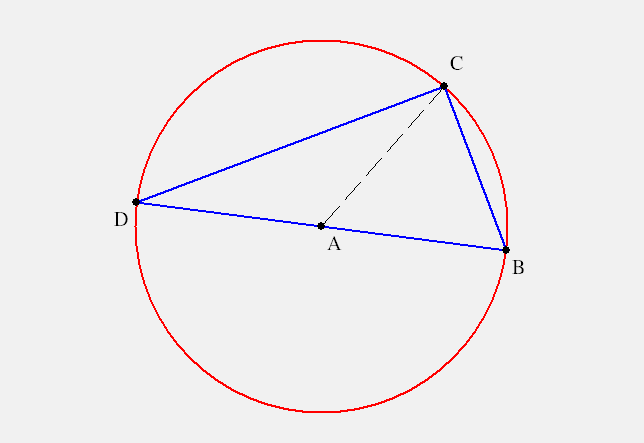
Proof. Let `A` be the center of a circle. First we consider the case where one side is a diameter. Let `DB` be a diameter. Then for a point `C` on the circle, `/_BAC` is an exterior angle of the isoceles △`DAC`.
|
Click image to view in KSEG. |
|
By the Exterior Angle Theorem of Euclid, we have
`/_BAC=/_ADC+/_DCA=alpha+alpha=2 alpha`. |
So the peripheral angle is half the central angle to the same secant `CB`.
Recall the Law of Sines from trigonometry:
|
Click image to view in KSEG. |
|
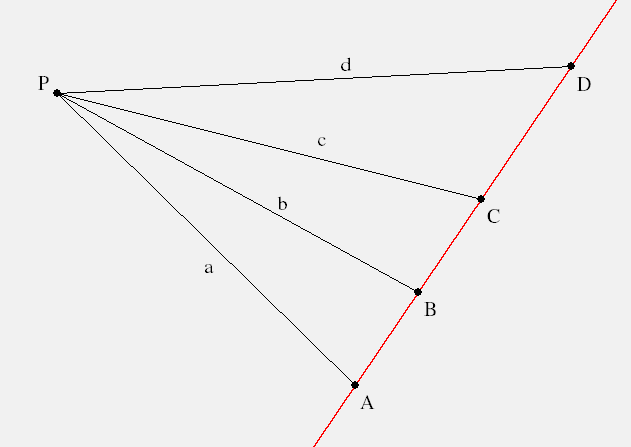
Proof of `(**)`. Apply the Law of Sines to △`ABP` then
`frac{A-B}{sin/_BPA}=frac{a}{sin/_B}=frac{b}{sin/_A}`, |
where `A-B` is the signed length `|A-B|` and `sin/_B=sin/_PBA=sin/_CBP` since supplementary angles have the same sine. Now let’s calculate
`frac{A-B}{A-D}\ frac{C-D}{C-B}\ =\ frac{A-B}{sin/_BPA}\ frac{C-D}{sin/_DPC}\ =\ frac{P-A}{sin/_B}\ frac{P-C}{sin/_D}`. |
`frac{sin/_BPA}{sin/_DPA}\ frac{sin/_DPC}{sin/_BPC}\ =\ frac{A-D}{sin/_DPA}\ frac{C-B}{sin/_BPC}\ =\ frac{P-A}{sin/_D}\ frac{P-C}{sin/_B}`. |
So `frac{A-B}{A-D}\ frac{C-D}{C-B}\ =\ frac{sin/_BPA}{sin/_DPA}\ frac{sin/_DPC}{sin/_BPC}\ \ square`.
A perspective ruler on a line with a finite vanishing point is obtained with the following procedure: given `l` with vanishing point `V`,
-
Choose a point `P` not on `l` on the extension of `l` past `V`.
-
Choose a line `s\ ||\ (PV)`.
-
On `s` choose a Euclidean ruler.
-
Transfer this scale through the lens `P` to `l`.

|
Click image to view in KSEG. |
|


